Аристотель расстояние до луны

На каком расстоянии Луна от Земли и как было измерено это расстояние?

Минимальное и максимальное расстояние между Землей и Луной, способы измерения расстояния до Луны и диаметра спутника нашей планеты

Как измеряли расстояние до планет в древности?

Представьте себя на месте человека не знакомого со строением Солнечной системы, наблюдающего за ночным небосводом. Звезды, сами по себе, вам представляются неподвижными объектами, но вот само звездное небо вроде как вращается, причем вращается вокруг Земли и совершает полный оборот за 24 часа.

Легко сделать вывод, располагая таким данными, что звезды “прикреплены” к небесному своду, представляющему собой своеобразное “покрывало”, окутывающее нашу планету со всех сторон. Это наблюдение очевидное и простое и потому, вплоть до самого XVII века – главенствующее и даже “научное”.

В то же время, уже в древности люди замечали, что некоторые небесные светила движутся среди звезд — а следовательно, эти светила не могли быть прикреплены к небесному своду и находились к Земле ближе, чем само небо. Насчитывалось семь таких небесных тел, называвшихся (в порядке их яркости) Солнце, Луна, Венера, Юпитер, Марс, Сатурн и Меркурий. Эти семь небесных тел греки называли «планетес» (скитальцы или “блуждающие звезды”), так мы до сих пор большинство из них и называем – «планеты».

Пропорции Земли и Луны – да, наш спутник не так уж и мал, всего в 4 раза уступая Земле по размеру. Впрочем, при этом он легче в 80 раз.

Дальнейшие наблюдения показали – можно установить, какие из планет находятся ближе к Земле, а какие — дальше от нее. Например, при каждом солнечном затмении Луна проходила между Землей и Солнцем и, следовательно, Луна была ближе к Земле, чем Солнце.

При оценке других расстояний древние исходили из относительной скорости движения планет среди звезд (чем ближе к нам предмет, тем более быстрым кажется его движение). Исходя из относительной скорости движения планет среди звезд, греки решили, что Луна расположена ближе к Земле, чем остальные планеты. Прочие же располагались в порядке увеличения расстояния так: Меркурий, Венера, Солнце, Марс, Юпитер и Сатурн.

Разумеется, в таком случае при определении расстояний от планет до Земли следовало начинать с ближайшего светила – то есть Луны.

Как Гиппарх измерил расстояние до Луны?

Первую серьезную попытку определить расстояние до Луны предпринял греческий астроном Аристарх Самосский (320—250 гг. до н. э.). Он опирался на наблюдения, сделанные во время лунного затмения. Когда тень Земли упала на Луну, по изгибу ее края можно было судить, как велико ее поперечное сечение по сравнению с размерами Луны.

Кажется, что Луна совсем близко от Земли. Вот так выглядит расстояние между Землей и Луной в натуральных пропорциях. 384 000 километров – не так и близко, а?

Считая, что Солнце находится от Земли гораздо дальше Луны, Аристарх с помощью несложных геометрических построении мог установить, как далеко должна Луна находиться от Земли, чтобы тень Земли уменьшалась до наблюдаемых размеров.

Этот метод был улучшен и дополнен примерно через 100 лет другим греческим астрономом — величайшим астрономом античности Гиппархом из Никеи (190— 120 гг. до н. э.). Гиппарх пришел к выводу, что расстояние от Земли до Луны примерно в 30 раз больше диаметра Земли. Если принять длину диаметра, предложенную Эратосфеном, т.е. 12 800 км, то в этом случае расстояние между Землей и Луной окажется равным 384 000 км.

Это блистательный результат, если учесть тогдашнее состояние астрономии. Наиболее точная современная цифра среднего расстояния между центрами Земли и Луны — 384 395 км. Не располагая и сотой долей тех возможностей, которыми располагает астрономия сейчас, Гиппарх из Никеи провел вычисления с погрешностью в 1/1000!

Как был измерен диаметр Луны

Конечно же, 384 395 километров – среднее расстояние между Землей и Луной, так как Луна движется вокруг Земли не по точному кругу: иногда она ближе к нашей планете, а иногда дальше.

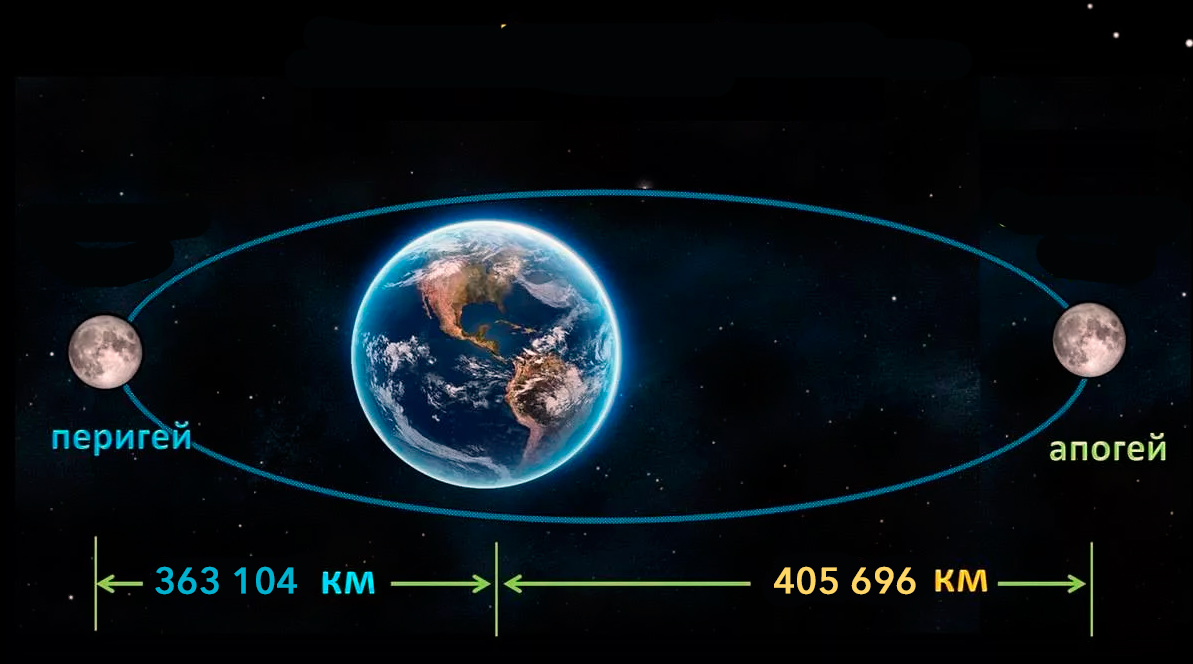
Минимальное расстояние между Луной и Землей (в перигее) равно 363 300 км, а максимальное (в апогее) —405 500 км.

Зная это расстояние, можно вычислить истинный диаметр Луны, исходя из ее видимых размеров. Он равен 3473,4 км, а окружность Луны, следовательно, составляет 10 900 км. Луна намного меньше Земли, но все же ее размеры весьма внушительны.

После того как было определено расстояние до Луны, с идеей о том, что небо находится почти над самыми нашими головами, было покончено навсегда. Оно отодвинулось на колоссальное расстояние, представлявшееся грекам немыслимым.

Даже ближайшее небесное тело оказалось почти в 400 000 км от Земли, а все другие, значит, находились от нее еще дальше и, возможно, намного дальше. Ни о какой “плоской Земле накрытой стеклянным куполом” больше не могли помыслить даже самые стойкие скептики.

Перигей и апогей Луны по отношению к Земле – самое близкое и самое дальнее расстояние между Луной и Землей

Источник

О размерах и расстояниях (Аристарх) — On the Sizes and Distances (Aristarchus)

О размерах и расстояниях (Солнца и Луны) (Περὶ μεγεθῶν καὶ ἀποστημάτων [ἡλίου καὶ σελήνης], Peri megethon kai apostematon ) широко признается как единственная сохранившаяся работа, написанная древним греком-астрономом Аристархом в 310 г. –230 г. до н. Э. В этой работе вычисляются размеры Солнца и Луны , а также их расстояния от Земли в единицах радиуса Земли.

Книга была предположительно сохранена студентами курса математики Паппа Александрийского , хотя свидетельств этого нет. В первое издание было опубликовано Джон Уоллис в 1688, используя несколько средневековых рукописей , собранных сэром Генри Сэвил . Самый ранний латинский перевод был сделан Джорджо Валла в 1488 Существует также 1572 латинский перевод и комментарий по Фредерико Commandino .

СОДЕРЖАНИЕ

Символы

Метод работы основывался на нескольких наблюдениях:

• Видимый размер Солнца и Луны на небе.
• Размер тени Земли относительно Луны во время лунного затмения
• Угол между Солнцем и Луной во время полумесяца очень близок к 90 °.

Остальная часть статьи детализирует реконструкцию метода и результатов Аристарха. Реконструкция использует следующие переменные:

Месяц

Аристарх начал с предположения, что во время полумесяца Луна образует прямоугольный треугольник с Солнцем и Землей. Наблюдая за углом между Солнцем и Луной, φ , отношение расстояний до Солнца и Луны может быть вычислено с помощью одной из форм тригонометрии .

Из диаграммы и тригонометрии мы можем вычислить, что

S L знак равно 1 потому что ⁡ φ знак равно сек ⁡ φ . <\ displaystyle <\ frac > = <\ frac <1><\ cos \ varphi>> = \ sec \ varphi.>

Диаграмма сильно преувеличена, потому что на самом деле S = 390 L , а φ очень близко к 90 °. Аристарх определил φ на тридцатую часть квадранта (в современных терминах, на 3 °) меньше прямого угла: в современной терминологии 87 °. Тригонометрические функции еще не были изобретены, но, используя геометрический анализ в стиле Евклида , Аристарх определил, что

18 S L 20. <\ displaystyle 18

Другими словами, расстояние до Солнца было где-то в 18-20 раз больше, чем расстояние до Луны. Это значение (или значения, близкие к нему) были приняты астрономами в течение следующих двух тысяч лет, пока изобретение телескопа не позволило более точную оценку солнечного параллакса .

Читайте также:  Когда будет два луны 2015

Аристарх также рассуждал, что, поскольку угловые размеры Солнца и Луны были одинаковыми, но расстояние до Солнца было в 18-20 раз дальше, чем Луна, Солнце, следовательно, должно быть в 18-20 раз больше.

Лунное затмение

Затем Аристарх использовал другую конструкцию, основанную на лунном затмении:

По подобию треугольников и D L знак равно т т — d <\ displaystyle <\ frac > = <\ frac

> \ quad> D S знак равно т s — т . <\ displaystyle \ quad <\ frac > = <\ frac >.>

Разделив эти два уравнения и используя наблюдение, что видимые размеры Солнца и Луны одинаковы , дает L S знак равно ℓ s <\ displaystyle <\ frac > = <\ frac <\ ell>>>

ℓ s знак равно т — d s — т ⇒ s — т s знак равно т — d ℓ ⇒ 1 — т s знак равно т ℓ — d ℓ ⇒ т ℓ + т s знак равно 1 + d ℓ . <\ displaystyle <\ frac <\ ell>> = <\ frac > \ \ \ Rightarrow \ \ <\ frac > = <\ frac <\ ell>> \ \ \ Rightarrow \ \ 1 — <\ frac > = <\ frac <\ ell>> — <\ frac <\ ell>> \ \ \ Rightarrow \ \ <\ frac <\ ell>> + <\ frac > = 1 + <\ frac <\ ell>>.>.

Крайнее правое уравнение может быть решено относительно ℓ / t

т ℓ ( 1 + ℓ s ) знак равно 1 + d ℓ ⇒ ℓ т знак равно 1 + ℓ s 1 + d ℓ . <\ displaystyle <\ frac <\ ell>> (1 + <\ frac <\ ell>>) = 1 + <\ frac <\ ell>> \ \ \ Rightarrow \ \ < \ frac <\ ell>> = <\ frac <1 + <\ frac <\ ell>>> <1 + <\ frac <\ ell>>>>.>.

т s ( 1 + s ℓ ) знак равно 1 + d ℓ ⇒ s т знак равно 1 + s ℓ 1 + d ℓ . <\ displaystyle <\ frac > (1 + <\ frac <\ ell>>) = 1 + <\ frac <\ ell>> \ \ \ Rightarrow \ \ <\ frac > = <\ frac <1 + <\ frac <\ ell>>> <1 + <\ frac <\ ell>>>>.>.>

Внешний вид этих уравнений можно упростить, используя n = d / ℓ и x = s / ℓ .

ℓ т знак равно 1 + Икс Икс ( 1 + п ) <\ displaystyle <\ frac <\ ell>> = <\ frac <1 + x>>> s т знак равно 1 + Икс 1 + п <\ displaystyle <\ frac > = <\ frac <1 + x><1 + n>>>

Приведенные выше уравнения полностью определяют радиусы Луны и Солнца в виде наблюдаемых величин.

Следующие формулы дают расстояния до Солнца и Луны в земных единицах:

L т знак равно ( ℓ т ) ( 180 π θ ) <\ displaystyle <\ frac > = \ left ( <\ frac <\ ell>> \ right) \ left ( <\ frac <180><\ pi \ theta>> \ right) > S т знак равно ( s т ) ( 180 π θ ) <\ displaystyle <\ frac > = \ left ( <\ frac > \ right) \ left ( <\ frac <180><\ pi \ theta>> \ right)>

где θ — видимый радиус Луны и Солнца, измеренный в градусах.

Маловероятно, что Аристарх использовал эти точные формулы, но эти формулы, вероятно, являются хорошим приближением к формулам Аристарха.

Полученные результаты

Приведенные выше формулы могут быть использованы для реконструкции результатов Аристарха. В следующей таблице показаны результаты давней (но сомнительной) реконструкции с использованием n = 2, x = 19,1 ( φ = 87 °) и θ = 1 °, наряду с современными принятыми значениями.

Количество	Связь	Реконструкция	Современное
с / т	Радиус Солнца в радиусах Земли	6,7	109
т / ℓ	Радиус Земли в радиусах Луны	2,85	3,50
Л / т	Расстояние Земля-Луна в радиусах Земли	20	60,32
S / т	Расстояние Земля-Солнце в радиусах Земли	380	23 500

Ошибка в этом вычислении происходит в первую очередь из-за плохих значений x и θ . Плохое значение θ особенно удивительно, поскольку Архимед пишет, что Аристарх был первым, кто определил, что Солнце и Луна имеют видимый диаметр в полградуса. Это даст значение θ = 0,25 и соответствующее расстояние до Луны в 80 радиусов Земли, что намного лучше. Несогласие в работе с Архимедом, по-видимому, связано с утверждением Аристарха о том, что лунно-солнечный диаметр составляет 1/15 «мероса» зодиака, что означает 1/15 зодиакального знака (30 °), не зная, что Греческое слово «мерос» означало либо «часть», либо 7 ° 1/2; и 1/15 последней суммы составляет 1 ° / 2, что согласуется с показаниями Архимеда.

Читайте также:  Когда будет луна светится

Аналогичная процедура была позже использована Гиппархом , который по оценкам среднего расстояния до Луны , как 67 радиусов Земли, и Птолемея , который принял 59 радиусов Земли для этого значения.

Иллюстрации

Некоторые интерактивные иллюстрации предложений в разделе « Размеры» можно найти здесь:

• Гипотеза 4 утверждает, что когда Луна кажется нам уменьшенной вдвое, ее расстояние от Солнца будет меньше квадранта на одну тридцатую квадранта [то есть меньше 90 ° на 1/30 от 90 ° или на 3 °. , и поэтому равен 87 °] (Heath 1913: 353).
• Предложение 1 утверждает, что две равные сферы охватываются одним и тем же цилиндром, а две неравные сферы — одним и тем же конусом, вершина которого находится в направлении меньшей сферы; и прямая линия, проведенная через центры сфер, проходит под прямым углом к ​​каждой из окружностей, в которых поверхность цилиндра или конуса касается сфер (Heath 1913: 354).
• Утверждение 2 гласит, что если сфера освещена сферой, большей, чем она сама, то освещенная часть первой сферы будет больше, чем полусфера (Heath 1913: 358).
• Утверждение 3 гласит, что круг на Луне, разделяющий темную и яркую части, является наименьшим, когда конус, охватывающий и Солнце, и Луну, имеет вершину у нашего глаза (Heath 1913: 362).
• Утверждение 4 гласит, что круг, разделяющий темную и яркую части на Луне, заметно не отличается от большого круга на Луне (Heath 1913: 365).
• Утверждение 6 гласит, что Луна движется [по орбите] ниже, чем [орбита] Солнца, и, когда она уменьшена вдвое, находится на расстоянии меньше квадранта от Солнца (Heath 1913: 372).
• Предложение 7 гласит, что расстояние от Солнца до Земли больше, чем в 18 раз, но меньше, чем в 20 раз, расстояния Луны от Земли (Heath 1913: 377). Другими словами, Солнце находится в 18-20 раз дальше и шире Луны.
• Утверждение 13 гласит, что прямая линия, соединяющая часть, пересеченную в пределах земной тени, окружности круга, в котором края круга, разделяющего темную и яркую части Луны, движутся меньше чем вдвое диаметра окружности. Луна, но имеет отношение к ней большее, чем отношение 88 к 45; и он составляет менее 1/9 части диаметра Солнца, но имеет отношение к нему больше, чем 21, к 225. Но у него есть прямая линия, проведенная из центра Солнца под прямым углом к ось и встречающиеся со сторонами конуса отношение больше, чем отношение 979 к 10 125 (Heath 1913: 394).
• Предложение 14 гласит, что прямая линия, соединяющая центр Земли с центром Луны, имеет прямую, отрезанную от оси к центру Луны прямой линией, проходящей через [окружность] в тени Земли a отношение больше, чем у 675 к 1 (Heath 1913: 400).
• Предложение 15 утверждает, что диаметр Солнца имеет отношение к диаметру Земли больше 19/3, но меньше 43/6 (Heath 1913: 403). Это означает, что Солнце (в среднем) в 6¾ раз шире Земли или что Солнце имеет ширину 13½ земного радиуса. Тогда Луна и Солнце должны быть на расстоянии 20¼ и 387 земных радиусов от нас, чтобы иметь угловой размер в 2º.
• Предложение 17a в средневековой арабской версии книги Ат -Туси о размерах утверждает, что отношение расстояния вершины теневого конуса от центра Луны (когда Луна находится на оси [то есть в середине затмение] конуса, содержащего Землю и Солнце) к расстоянию от центра Луны до центра Земли больше отношения 71 к 37 и меньше отношения 3 к одному (Berggren & Sidoli 2007: 218). Другими словами, кончик теневого конуса Земли находится между 108/37 и в четыре раза дальше, чем Луна.

Источник