Чему равна гравитационная постоянная солнца

ГРАВИТАЦИОННАЯ ПОСТОЯННАЯ — коэффициент пропорциональности G в ф-ле, описывающей закон всемирного тяготения Ньютона,

где F — сила, с к-рой точечные массы m₁ и m₂, находящиеся на расстоянии r друг от друга, взаимно притягиваются.

Численное значение и размерность Г. п. зависят от выбора единиц массы, длины и времени (табл. 1).

Табл. 1. — Значения гравитационной постоянной

Наименование и обозначение	Единицы			Численное значение
Наименование и обозначение	длина	масса	время	Численное значение
Кавендишева Г.п. *, G	м	кг	с	(6,6745+0,0008) . 10 -11 м 3 /(кг . с 2 )
Геоцентрическая Г.п.,	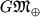м	масса Земли	с	(398 600,5+0,3) . 10 9 м 3 /с 2
Гелиоцентрическая Г.п.,	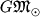м	масса Солнца	с	(132 712 438+5) . 10 12 м 3 /с 2
Селеноцентрическая Г.п.,	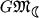м	масса Луны	с	(4902,7+0,1) . 10 9 м 3 /с 2
Гауссова Г.п., k	а.е.	масса Солнца	эфемеридные сутки	0,01720209895
Эйнштейнова Г.п.,	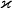м	кг	—	(1,8664+0,0002) . 10 -26 м/кг
* Значение Г.п. приведено по определениям ГАИШ.

Г. п. G, имеющую размерность [L] 3 [M] -1 [T] -2 , где масса М, длина L и время Т выражены в единицах Международной системы единиц (СИ), иногда называют кавендишевой Г. п. в честь англ. учёного Г. Кавендиша, к-рый в 1798 г. впервые в лабораторном эксперименте с крутильными весами определил значение G. Все лабораторные эксперименты по определению G можно условно разделить на две группы.

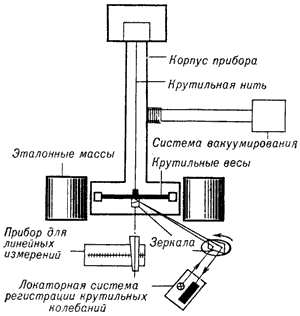
В первой группе экспериментов сила гравитац. взаимодействия сравнивается с упругой силой нити горизонтальных крутильных весов. Они представляют собой лёгкое коромысло, на концах к-рого укреплены пробные массы. За середину коромысло подвешено на тонкой упругой нити. Величина гравитац. взаимодействия определяется по углу закручивания нити (статич. метод), вызванному притяжением пробных масс к расположенным вблизи эталонным массам.

Во второй группе сила гравитац. взаимодействия между пробными и эталонными массами сравнивается с силой тяжести, для чего используются рычажные весы. Этим способом Г. п. была впервые определена нем. физиком Ф. Йолли в 1878 г. Впоследствии опыты Кавендиша и Йолли неоднократно повторялись, однако в наше время они представляют лишь исторический интерес.

Значение Г. п., включённое Международным астрономическим союзом (MAC) в Систему астрономических постоянных (САП) 1976 г., к-рым продолжают пользоваться, получено с помощью крутильных весов в 1942 г. П. Хейлом и П. Хржановским (США).

В СССР Г. п. впервые была определена в Государственном астрономическом институте имени П. К. Штернберга (ГАИШ) в 1975-78 гг. Как и в экспериментах Хейла и Хржановского, был применён динамич. метод, сущность к-рого состоит в следующем. Частота крутильных колебаний w горизонтальных весов в гравитац. поле эталонных масс определяется выражением:

Частота w измеряется в процессе эксперимента, величины m и J могут быть вычислены. Коэфф. m зависит от размеров и плотностей эталонных масс и крутильных весов, а также от их взаимного расположения. Момент инерции крутильных весов J определяется их геометрич. размерами и массой. Остаются два неизвестных параметра — крутильная жесткость t и Г. п. Поэтому для исключения t и определения G нужно иметь два таких ур-ния (т. е. провести измерения w по крайней мере для двух различных положений эталонных масс). Т. о., для определения Г. п. динамич. методом необходимо произвести измерения: 1) геометрич. размеров и плотностей эталонных масс и крутильных весов; 2) положения эталонных масс относительно крутильных весов; 3) частот крутильных колебаний при различных положениях эталонных масс.

Схема экспериментальной установки
ГАИШ (динамический метод определения G).

На рис. приведена схема экспериментальной установки ГАИШ. Т. к. параметры, приведённые в пункте 1), не меняются от эксперимента к эксперименту, то их измерение достаточно провести один раз для всех экспериментов. Измерения остальных параметров должны производиться в каждом эксперименте. Т. о., для получения одного значения Г. п. при разных положениях эталонных масс (перестановка эталонных масс в процессе эксперимента производится автоматически) определяются расстояния между эталонными и пробными массами (с помощью прибора для линейных измерений), а фотоэлектрич. система регистрации измеряет частоту крутильных колебаний. Такие эксперименты повторяются многократно, поэтому для уменьшения случайных погрешностей вычисляют ср. значение Г. п. и его среднеквадратическую погрешность.

Во всех совр. определениях Г. п. (кавендишевой) были использованы крутильные весы. Помимо собственно динамич. метода применялись также его модификации — резонансный и ротационный методы. В резонансном методе эталонные массы вращаются вокруг оси крутильной нити с частотой, равной частоте собственных колебаний весов, что приводит к резонансному возбуждению крутильных колебаний. По изменению амплитуды колебаний можно судить о величине Г. п. В ротационном методе платформа, на к-рой установлены крутильные весы и эталонные массы, вращается вокруг вертикальной оси. Г. п. определяется по измерениям ускорения платформы, а также постоянного угла поворота крутильных весов относительно эталонных масс.

Результаты совр. определений Г. п. приведены в табл. 2. Среднеквадратические погрешности измерений указывают на внутр. сходимость каждого результата. Лучшие из них (три последних результата) не перекрываются между собой в доверительных интервалах. Это связано с тем, что определение кавендишевой Г. п. требует проведения абс. измерений, и поэтому в отдельных результатах возможны систематич. погрешности. Очевидно, значение Г. п. может быть достоверным только при учёте различных определений Г. п., полученных разными методами.

Табл.2. — Результаты современных определений кавендишевой гравитационной постоянной.

Авторы, место проведения измерений, год публикации	Метод	Значение Г.п., 10 -11 м 3 /(кг . с 2 )
Хейл, Хржановский (США), 1942	Динамический	3,373+0,005
Роуз, Паркер, Бимс и др. (США), 1969	Ротационный	6,674+0,004
Реннер (Венгрия), 1970	Динамический	6,670+0,008
Фаси, Понтикис, Лукас(Франция), 1972	Резонансный	6,6714+0,0006
Сагитов, Милюков, Монахов и др. (1978)	Динамический	6,6745+0,0008
Лютер, Тоулер (США), 1982	Динамический	6,6726+0,0005

Г. п., выраженные в астрономич. единицах, определяются на основании астрономич. наблюдений и 3-го закона Кеплера, к-рый явл. следствием закона тяготения (1).

Геоцентрическая Г. п. (равная произведению кавендишевой Г. п. на массу Земли ) используется при расчётах движения в поле тяготения Земли небесных тел, как естественных, так и искусственных. Наиболее точно геоцентрич. Г. п. определяется по наблюдениям ИСЗ или КА, направляемых к др. планетам, т. к. на их движение меньше влияет неоднородность плотности Земли и неправильность её фигуры.

Аналогично гелиоцентрическая, селеноцентрическая и др. планетоцентрические Г. п. предназначены для расчёта движения в гравитац. полях соответственно Солнца, Луны и планет. В астрономии применяется и иной подход к определению Г. п. Ей априорно приписывается нек-рое фиксированное значение; две из трёх физ. величин (масса и время), задающих размерность Г. п., определяются из наблюдений, тогда ед. длины становится производной величиной. Так вводится гауссова Г. п. k. По мере уточнения массы Солнца (ед. массы) и эфемеридных суток (ед. времени) изменяется величина а. е.

Эйнштейнова Г. п. используется в теоретич. физике. Она связана с кавендишевой Г. п. соотношением: .

Как в теории тяготения Ньютона, так и в общей теории относительности (ОТО) А. Эйнштейна Г. п. рассматривается как универсальная константа природы, не изменяющаяся в пространстве и времени и не зависящая от физ. и хим. св-в среды и гравитирующих масс. Существуют варианты теории гравитации, имеющие в слабых полях одинаковый ньютоновский предел, но дающие ряд предсказаний, отличных от предсказаний ОТО, в т. ч. переменность Г. п. Напр., теория П. Дирака, созданная ещё в 1930-е гг., предсказывает изменение Г. п. ( D G) со временем на величину

D G/G » 6 . 10 -11 в год. Нек-рые варианты теории гравитации предполагают зависимость Г. п. от расстояния между притягивающимися телами. Однако имеющиеся наблюдательные данные, а также специально поставленные лабораторные эксперименты пока не позволяют обнаружить это гипотетич. изменение Г. п.

Лит.: Сагитов М. У., Постоянная тяготения и масса Земли, М., 1969; Новое определение кавендишевой гравитационной постоянной, «ДАН СССР», 1979, т. 245, № 3, с. 567-69; Абалакин В. К., Основы афемеридной астрономии, М., 1979.

Источник

Все самое интересное что нужно знать о гравитационной постоянной

В современной формулировке закона всемирного тяготения присутствует коэффициент , называющийся гравитационной постоянной и стоящий перед формулой особняком. Интересно, что Ньютон, открывший закон притяжения, не использовал явную форму константы, численно она была определена больше века спустя со дня смерти учёного.

Что такое и чему равна гравитационная постоянная

Формула закона всемирного тяготения, известная по курсу школьной механики:

G – коэффициент пропорциональности или гравитационная постоянная;

m_1, m₂ – массы двух тел, испытывающих взаимное притяжение;

r – расстояние между ними.

Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:

Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.

В чём измеряется гравитационная постоянная

Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной – , но её возникновение легко объясняется.

Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём

то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.

После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.

То есть единица измерения гравитационной силы –

и размерность не совпадает с привычной . Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.

Проведём математические вычисления самостоятельно.

Нужно уравнять и .

Для этого нужно разделить на 1с 2 и 1кг, а также умножить на м 3 , получим:

Получилась требуемая размерность.

Следовательно, постоянная имеет размерность .

Как найти гравитационную постоянную – история открытия

Коэффициент G – универсальная константа, измерение которой осуществляется экспериментальным путём. Доподлинно неизвестно, кто открыл значение гравитационной постоянной, первое употребление в «Трактате по механике» Пуассона датируется 1811 годом.

Работы Ньютона

При публикации закона тяготения в трактате Ньютона отсутствовало явное обозначение константы, характеризующее гравитацию и её действие. Коэффициент не появлялся в работах по физике вплоть до конца восемнадцатого века, его точное значение не было вычислено.

Вместо известной сегодня постоянной присутствовал гравитационный параметр:

M – масса объекта, причём, масса планеты или звезды, так как гравитационный параметр нашёл широкое распространение в астрофизике.

Сегодня для объектов Солнечной системы значение параметра рассчитано точнее, чем гравитационная постоянная G и масса по отдельности, так как она не требует серьёзных экспериментов, вычисляется на основании астрономических наблюдений.

для Земли ;
Луны ;
Солнца .

Подробнее о использовании закона всемирного тяготения в астрономии вы можете прочитать в нашей статье.

Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша

Естествоиспытатель Джон Митчел придумал эксперимент для определения массы Земли при помощи крутильных весов, однако не реализовал его. После его смерти идея опыта и аппаратура перешли к английскому физику и химику Генри Кавендишу, который, усовершенствовав прибор, провёл ряд экспериментов и осуществил задумку своего предшественника.

Главенствующая роль в опытах отводилась установке. На метровой нити из меди подвешивалось коромысло длиной 1,8 метра, на его концах устанавливалась пара свинцовых шариков диаметром 5 сантиметров, массой 775 грамм. Чуть выше крепилась поворотная ферма, причём тщательно соблюдалось требование совпадения оси вращения фермы с медной нитью. На концах поворотной штанги находилось по одному большому свинцовому шару диаметром 20 сантиметров, массой 49,5 килограмм. Чтобы избежать влияния конвекционных воздушных потоков, вся установка накрывалась плотным деревянным кожухом. Вследствие взаимодействия лёгкие шарики притягивались к тяжёлым, закручивая нить и отклоняя коромысло. Угол отклонения фиксировался двумя телескопами, а сила упругости нити приравнивалась гравитационному взаимодействию шаров.

Величина определённой силы притяжения составляла 0,17 микроньютона. Если сравнивать это значение с весом маленького шара, то оно меньше последнего примерно в 45 миллионов раз.

В результате своего эксперимента Генри Кавендиш рассчитал среднюю плотность Земли, причём его эксперимент был точным – погрешность измеренного значения в сравнении с современным значением составляет всего 0,7%. Именно Кавендишу приписывают открытие значения гравитационной постоянной, однако он никогда не задавался подобной целью при проведении своих опытов. Очевидно, величина константы определена на основании результатов его эксперимента, но кто сделал это первым, неизвестно.

Измерение гравитационной постоянной

Значение константы, полученное по измеренной Кавендишем плотности, по разным источникам разнится. Британская энциклопедия называет число, равное , с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно , а Олег Павлович Спиридонов в сборнике постоянных приводит значение .

Коэффициент пропорциональности определяли после Генри Кавендиша, причём зачастую его установку модернизировали новыми материалами. Например, в 1872 году Корню и Байль для измерения гравитационной постоянной использовали платиновые маленькие шарики и стеклянные, наполненные ртутью, большие. Результаты опыта показали значение

с относительной погрешностью 5*10 -3 .

Современная история изменений гравитационной постоянной

Гравитационная постоянная – десятичная дробь, её значение постоянно уточняется, причём измерение коэффициента G происходит путём усовершенствования прибора Митчела и улучшения методов наблюдения. Например, в 2018 году учёные из России и Китая проводили опыты на установках разной конструкции. В первой группе применялся метод «time of swing» (TOS), где коэффициент пропорциональности зависит от колебательной частоты весов. Во второй – метод «angular acceleration feedback» (AAF), где угловое ускорение независимо вращающихся коромысел шаров измеряется системой управления с обратной связью, при этом нить поддерживается незакрученной.

По результатам команды первый метод продемонстрировал значение гравитационной постоянной , второй метод – . Относительная погрешность составила 11,6*10 -6

Комитет по данным для науки и техники (CODATA) рекомендовал на 2020 год значение коэффициента пропорциональности, равное:

Таким образом, гравитационная постоянная всё время уточняется, требуя новые, более точные способы измерения и вычисления.

Источник