Черная пластина освещаемая солнцем

В этой задаче необходимо использовать разумные предложения (которые, впрочем, формулируется в форме строгих физических законов).

Пусть освещенная сторона пластинки поглощает в единицу времени энергию $q_<0>$. В состоянии теплового равновесия эта энергия излучается в окружающую среду как с освещенной $(q_<1>)$, так и с затемненной $(q_<2>)$ стороны. Причем можно считать, что количество отданной теплоты пропорционально разности температур поверхности и окружающего воздуха.
Запишем условия теплового баланса

$q_ <0>= q_ <1>+ q_ <2>= a(T_ <1>— T_<0>) + a(T_ <2>— T_<0>)$, (1)

где $a$ — некоторая постоянная в рамках нашей задачи величина. Количество теплоты $q_<2>$, излучаемое затемненной стороной, переноситься внутри пластины. Этот поток теплоты пропорционален скорости изменения температуры с расстоянием

$q_2 = k \frac — T_<2>> = a (T_ <2>— T_<0>)$, (2)

где $d$ — толщина пластины, $k$ — некоторый постоянный коэффициент (он называется теплопроводностью), зависящий от свойств материала, из которого изготовлена пластина. Аналогичные соотношения можно записать для пластины толщиной $2d$.

где $T_<2>^< \prime>$ и $T_<1>^< \prime>$ — температуры освещенной и неосвещенной сторон пластины вдвое большей толщины.

Совместное решение системы уравнений (1)-(4) приводит к результату

Источник

Черная пластина освещаемая солнцем

Равновесная температура

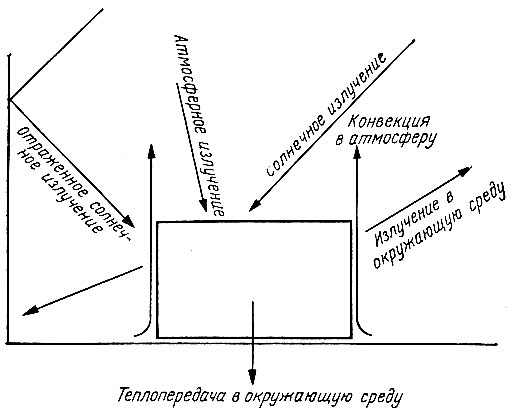
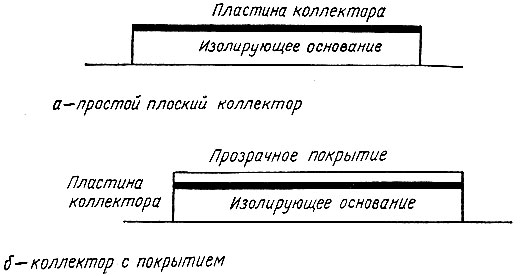
Итак, вернемся к рассмотрению тела, освещаемого солнцем (рис. 18). Рис. 18 показывает, сколь многообразны пути, посредством которых тело приобретает и теряет энергию. Чтобы нам было легче понять поведение такого тела, сначала несколько упростим наблюдаемую картину. Предположим, что интересующее нас тело представляет собой тонкую пластину, лежащую на теплоизолирующем основании (рис. 19, а). Здесь мы встречаемся с элементами так называемого плоского солнечного коллектора. Получая энергию от солнца, такое устройство вновь излучает ее, не обмениваясь излучением с окружающей средой. В данном случае мы пренебрегаем теплообменом с атмосферой через конвекцию и лучеиспускание, которые рассмотрим позже.

Рис. 18. Потоки солнечной энергии, падающие на облучаемое тело и отраженные им

Обозначим интенсивность солнечного излучения через P, а поглощательную способность пластины для этого вида радиации через α_c. Под действием солнечного излучения пластина нагревается до тех пор, пока не достигнет равновесной температуры T. При такой температуре интенсивности падающего и испускаемого излучения равны, что позволяет записать равенство

где ε — излучательная способность нашей пластины при низких температурах. Тогда равновесную температуру T мы получим из уравнения

Рис. 19. Плоские солнечные коллекторы

Очевидно, равновесная температура тем выше, чем больше отношение α_c /_ε. Судя по данным табл. 2, это отношение иногда, в частности для полированных металлов, достигает значений 2-3, но чаще оно много меньше. Однако полированные металлы вследствие их низкой поглощательной способности непригодны для изготовления коллекторов солнечного излучения. Для подобных целей обычно выбирают материалы с высокой поглощательной способностью, для которых отношение α_c /_ε близко к 1. Мы будем называть такие материалы нейтральными поглотителями (происхождение названия станет ясно из дальнейшего изложения). Полагая P = 800 Вт /_{м 2} (типичная интенсивность солнечного излучения в тропиках в летнее время), из уравнения (4.17) мы находим значение равновесной температуры, равное 343 K (70° С). Как оказалось, несмотря на приближенный характер наших оценок, эта величина действительно близка к реальной температуре черной пластины, установленной на длительное время под тропическим солнцем.

Теперь несколько усложним картину, в частности учтем такой важный фактор, как тепловые потери в воздухе, обусловленные конвекцией. Механизм этого явления прост. Соприкасаясь с горячей поверхностью, воздух нагревается и расширяется; его плотность уменьшается, и он плавно поднимается вверх. На смену приходят другие более прохладные и плотные слои воздуха, в результате возникает конвективное воздушное течение. (Благодаря преломлению света, обусловленному изменениями плотности воздуха, это течение мы часто можем наблюдать визуально.) При неподвижном воздухе интенсивность конвективных тепловых потерь для малой горизонтальной или слегка наклонной поверхности составляет около 4 Вт /_{м 2} на каждый градус разности температур поверхности и воздуха, хотя строгой пропорциональности между тепловыми потерями и разностью температур в действительности не наблюдается. При интенсивном движении воздуха над поверхностью, например при ветре, тепловые потери значительно возрастают. Так, при скорости . ветра около 10 м/с и малой разности температур интенсивность тепловых потерь на конвекцию достигает 30 Вт /_{(м 2 *K)}. Все эти значения мы должны принимать как экспериментальные результаты. Конвекционные потери можно оценить и теоретически, но теория этих процессов столь сложна, что мы не будем излагать ее здесь, дабы не осложнять нашего повествования.

Другим важным фактором, влияющим на собирание солнечной энергии, является длинноволновое излучение, приходящее из атмосферы. Оно испускается главным образом молекулами углекислого газа и водяного пара при поглощении ими прямого солнечного излучения, а также излучения, отраженного от земли и обусловленного конвекцией. Спектры поглощения этих молекул, связанные с их колебательными и вращательными движениями, лежат в видимой и инфракрасной областях. Перед испусканием энергия частично перераспределяется, однако в спектре атмосферного излучения вполне отчетливо проявляются линии и полосы, соответствующие длинам волн поглощения.

Общая интенсивность P_а этого излучения существенно зависит от содержания в атмосфере водяного пара, особенно вблизи земной поверхности. При повышенной влажности и сплошной облачности атмосфера ведет себя примерно так же, как черное тело с температурой около 280 K (10° С); соответствующая интенсивность излучения на горизонтальной поверхности составляет около 300 Вт /_{м 2} . На широтах Англии длинноволновое атмосферное излучение иногда достигает этой величины. При безоблачном небе в условиях засушливого климата распределение атмосферного излучения по длинам волн оказывается менее упорядоченным; поглощение, обусловленное молекулами CO₂, сосредоточено в узкой полосе вблизи 15 мкм, тогда как полосы поглощения, связанные с молекулами H₂O, разбросаны в интервале длин волн 20-100 мкм. Тем не менее общая интенсивность атмосферного излучения редко падает ниже 100 Вт /_{м 2} . Это весьма существенная радиация, благодаря которой ночью на поверхности Земли поддерживается приемлемая температура. В отсутствие подобного излучения температура земной поверхности в ночные часы должна резко падать (вследствие излучения энергии в пространство), как это и наблюдается на Луне, где атмосфера отсутствует. Температура поверхности Земли в течение ночи иногда снижается настолько, что появляется иней, но, за исключением полярных районов, она редко опускается ниже 0° С.

Теперь ясно, почему выше с помощью уравнения (4.17) мы получили удовлетворительное значение равновесной температуры (70° С), хотя и не учитывали теплообмен с атмосферой. При температуре окружающей среды, равной 17° С, и интенсивности конвективных потерь примерно 4 Вт /_{м 2 *°С} эти потери оцениваются примерно в 212 Вт /_{м 2} , что как раз компенсируется длинноволновым атмосферным излучением.

Источник

А.В. Быков, И.В. Митин, А.М. Салецкий — Оптика. Методика решения задач, страница 29

Описание файла

PDF-файл из архива «А.В. Быков, И.В. Митин, А.М. Салецкий — Оптика. Методика решения задач», который расположен в категории «книги и методические указания». Всё это находится в предмете «физика» из четвёртого семестра, которые можно найти в файловом архиве МГУ им. Ломоносова. Не смотря на прямую связь этого архива с МГУ им. Ломоносова, его также можно найти и в других разделах. .

Просмотр PDF-файла онлайн

Текст 29 страницы из PDF

МЕТОДИКА РЕШЕНИЯ ЗАДАЧгде σ = 5,67 ⋅ 10−8 Вт⋅м−2⋅К−4. Кроме того, с учетом (11.17) и (11.18):c ⋅u,(11.29)4где L0 − энергетическая яркость излучения с поверхности абсолютно черного телаuL0 =c.4πЛогично, что L0 и L из (11.16) одинаковы.ε0 (T ) = πL0 =11.2. Задачи с решениямиЗадача 11.2.1. Определить мощность излучения абсолютночерного тела, нагретого до температуры 1000 К, если площадь егоповерхности S равна 10 м2.РешениеПоскольку мощность РS и интенсивность I излучения связанысоотношением (11.13), то:PS = I ⋅ S .Согласно (11.28) для абсолютно черного тела:I = ε0 (T ) = σT 4 .Поэтому искомая мощность РS равнаPS = σT 4 S = 5,67 ⋅ 10−8 (1000 ) ⋅ 10 = 5,67 ⋅ 105 Вт.Ответ: 567 кВт.4Задача 11.2.2.

Черная пластина, освещаемая Солнцем, ориентирована перпендикулярно его лучам. Определить освещенностьпластины, если ее температура равна 300 К.РешениеСогласно (11.12) и (11.13), количество световой энергии, падающей на поверхность пластины площади S за время Δt , равноΔWпад = E ⋅ S ⋅ Δt ,где Е − освещенность пластины.Поскольку пластина черная, то энергия, излучаемая пластинойс обеих поверхностей за то же время, равна237Гл.

11. Тепловое излучениеΔWизл = ε0 ⋅ 2S Δt ,где ε0 − светимость абсолютно черного тела, которая зависит оттемпературы по закону (11.28):ε0 (T ) = σT 4 .В установившемся режиме:ΔWпад = Ризл ,илиE ⋅ S Δt = σ ⋅ T 4 ⋅ 2S ⋅ Δt ,откудаE = 2σT 4 = 2 ⋅ 5,67 ⋅ 10−8 ( 300 ) ≈ 919 Вт/м2.Ответ: Е = 919 Вт/м2.4Задача 11.2.3. Определить мощность излучения абсолютночерного тела, если площадь излучающей поверхности тела равна3м2, а максимум спектральной плотности излучения приходится надлину волны 0,58 мкм.Решение:Мощность PS излучения черного тела с площади поверхности SравнаPS = ε0 (T ) ⋅ S ,где, согласно (11.28), светимость абсолютно черного тела:ε0 (T ) = σT 4 .С учетом закона смещения Вина (11.8):λ maxT = bнаходим мощность излучения абсолютно черного тела44−2⎛ b ⎞−8 ⎛ 0 , 29 ⋅ 10 ⎞⋅=5,6710PS = σ ⎜S⋅⋅ 3 ≈ 106 МВт.⎜⎜⎟−6 ⎟⎟0,5810⋅⎝ λ max ⎠⎝⎠Ответ: РS=106 МВт.Задача 11.2.4.

С нагретой до некоторой температуры поверхности тела излучается энергия 175 Вт⋅см–2. При этом отношениеэнергетической светимости этой поверхности ε (T ) к светимости238ОПТИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧповерхности абсолютно черного тела ε0 (T ) , нагретого до той жетемпературы, равна α =ε (T )ε0 (T )= 0 ,5 . Найти температуру поверхно-сти тела.РешениеСогласно (11.28) энергетическая светимость поверхности черного тела определяется его температурой:ε0 (T ) = σT 4 ,где σ = 5,67 ⋅ 10−8 Вт ⋅ м -2 ⋅ К −4 . Следовательно,ε0σ0Так как по условию задачи: ε (T ) = 2 ⋅ 175 = 350 Вт см 2 , тоT =4T == 4350 ⋅ 1045,67 ⋅ 10−8≈ 2800 К.Ответ: Т = 2800 К.Задача 11.2.5. Определить плотность потока энергии солнечного излучения на земной орбите.

Температуру Солнца считатьравной 6000 К. Солнечный диск виден с Земли под углом 32′.РешениеПолагая, что Солнце излучает как абсолютно черное тело, дляпотока теплового излучения с его поверхности можем записать:PS = ε0 (T ) ⋅ S = σT 4 ⋅ πD 2 ,где D − диаметр Солнца. Если пренебречь потерями энергии излучения на пути от Солнца до Земли, то на земной орбите искомаяплотность потока энергии равнаPI ( R) = S 2 ,4πRгде R − расстояние от Земли до Солнца. Учитывая, что по условиюD/R = θ = 32′, получаем:2ВткВт⎛θ⎞I ( R ) = σT 4 ⎜ ⎟ ≈ 0 ,16 2 = 1,6 2 .⎝2⎠смм239Гл. 11.

Тепловое излучениеОтвет: I = 1,6кВтм2.Задача 11.2.6. Две большие полости с зеркально отражающиминаружными поверхностями имеют относительно малые круглыеотверстия диаметром d = 2 см, которые расположены друг напротив друга. В одной из полостей поддерживается постоянная температура T1 = 2000 К, в другой полости в установившемся режиметемпература равна T2 = 400 К.

Определить расстояние между отверстиями.РешениеБудем рассматривать отверстие в полости 1 как элемент поверхности абсолютно черного тела, имеющего температуру Т1. Всоответствии с (11.28) и (11.29), яркость излучения с такой поверхности:σT 4L= 1 ,πа согласно (11.14), поток энергии, попадающий в отверстие полости 2, равенP12 =πd 2Lcosθ ⋅ d Ω ,4 Ω∫где Ω − телесный угол, под которым отверстие в полости 2 видно споверхности отверстия в полости 1. Вычисляя интеграл в предыдущей формуле, получим:P12 =πd 242π∫0θd ϕ∫ Lcosθsinθ ⋅ d θ =0σT 4 θ2πd 2,2π 1π 24где θ ≈ d (2l ) .

Таким образом,2πd 2⎛ d ⎞σT14 ⎜⎟ .4⎝ 2L ⎠С другой стороны, поток энергии из полости 2 через отверстие в ней:P12 =πd 2σT24 .4В установившемся режиме:P12 = P2 ,P2 =240ОПТИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧи следовательно,2⎛ d ⎞4T14 ⎜⎟ = T2 .L2⎝⎠Поэтому искомое расстояние между отверстиями2 ( 2000 )L= 2 = ⋅= 25 см.2T2 2 ( 400 )2dT122Ответ: L = 25 см.Задача 11.2.7. Показать с помощью формулы Вина (11.6), чтомаксимальное значение спектральной плотности энергии тепловогоизлучения пропорционально Т3.РешениеСогласно формуле Вина (11.6)⎛ ω⎞uω (T ) = ω3 f ⎜ ⎟ .⎝T ⎠При фиксированной температуре производная∂uωf′= 3ω2 f + ω3∂ωTобращается в нуль, если3 f ( ωmax )ω = ωmax = −T.f ′ ( ωmax )Таким образом,Ответ: ( uω )max ∼ T 3 .Замечание. Для спектральной плотности uλ формула Винаимеет вид (11.7):ϕ ( λТ )uλ ( T ) =,λ5поэтому с учетом закона смещения (11.8):( uλ )max

T 5 .Задача 11.2.8.

Медный шарик диаметром d помещен в откачанный сосуд, температура стенок которого поддерживается близ-241Гл. 11. Тепловое излучениекой к абсолютному нулю. Начальная температура шарика Т0 = 400К. За время Δt=4 часа температура шарика уменьшается в η = 2раза. Считая поверхность шарика абсолютно черной, определитьего диаметр d.РешениеПри температуре Т за время dt с поверхности шарика излучается энергияdW = σT 4 ⋅ πd 2 ⋅ dt .В результате этого внутренняя энергия шарика изменяется навеличинуdU = c ⋅ m ⋅ dT ,где m − масса шарика, с − удельная теплоемкость.ПолагаяdW = dU ,получаем уравнение:σT 4 ⋅ πd 2 ⋅ dt = c ⋅ ρ ⋅πd 3⋅ dT ,6где ρ − плотность шарика.Разделяя переменные и интегрируя по t и T, находим:cρdΔt =η3 − 1 .318σT0ДжгТак как для меди с = 390и ρ = 8,9 3 , то для диаметра dкг ⋅ Ксмполучаем(d=18 ⋅ Δt ⋅ σ ⋅ T03( η3 − 1) cρ)18 ⋅ 4 ⋅ 60 ⋅ 60 ⋅ 5,67 ⋅ 10−8 ( 400 )3=( 8 − 1)2 ⋅ 390 ⋅ 8,9 ⋅103≈ 0 ,55 см.Ответ:d = 0,55 см.Задача 11.2.9.

Найти с помощью формулы Планка число фотонов dN в единице объема при температуре Т для спектральных интервалов ( ω,ω + d ω) и ( λ ,λ + d λ ) .РешениеСогласно (11.2):du ( ω,ω + d ω) = uωd ω ,242ОПТИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧгде в соответствии с формулой Планка (11.9):uω =ω22 3π cω.ωkTexp − 1Так как энергия фотона c частотой ω равна ω , тоdu ( ω,ω + d ω) = dN ⋅ ω .Следовательно, число фотонов в единице объема при температуре Т:ω2dω.dN ( ω,ω + d ω) = 2 3 ω (kT )π c e−1Делая замену переменных:ω = 2 πc λи2πcdω = 2 dλ ,λдля интервала ( λ ,λ + d λ ) получим:dN ( λ ,+ d λ ) =8πλ4dλ2 πce kT λ.−1Ответ:dN ( ω,ω + d ω) =ω22 3π cdωωkTe, dN ( λ ,λ + d λ ) =−18πλ4dλ2 πce kT λ.−1Задача 11.2.10.

При каких температурах расхождение междузначениями uω, рассчитанными по формулам Вина (11.11) и формуле Планка (11.9), для видимой части спектра ( 400 ≤ λ ≤ 750 нм )не превышает 1%?РешениеПо формуле Вина (11.11):uω =а по формуле Планка (11.9):ω32 3π ce−ω ( kT ),243Гл. 11. Тепловое излучениеuω =ω22 3π c eωω ( kT )−1.ПоэтомуuВинex −1= x ,uПланкeω hc=.kT λkTПо условию задачи:uПланк − uВин 1= x ≤ 0 ,01 ,uПланкeследовательно,hcT≤≈ 4150 K .λk ln100где x =Ответ: Для видимой части спектра (400 ≤ λ ≤ 750) Т ≤ 4150 Кдля λ = 750 нм.Задача 11.2.11. Световая мощность излучения точечного изотропного монохроматического (λ = 589 нм) источника равна 10 Вт.Найти: а) среднюю плотность потока фотонов на расстоянии r == 2 м от источника; б) расстояние R от источника до точки, гдесредняя концентрация фотонов равна 100 см−3.Решение:а) В соответствии с (11.13) на расстоянии r от точечного источника интенсивность излучения равнаP.I (r ) =4πr 2где P – излучательная мощность источника.Поскольку энергия одного фотона равна ε = hc λ , то средняяплотность потока фотонов на расстоянии r от источника:Pλ.j (r ) =4πr 2 hcПри r = 2 мj ≈ 6 ⋅ 1017 м −2 ⋅ с −1 .б) В случае точечного источника можно считать, что244ОПТИКА.

МЕТОДИКА РЕШЕНИЯ ЗАДАЧj (R ) = n( R ) ⋅ c ,где n(R ) − концентрация фотонов на расстоянии R от источника.ПоэтомуPλR=4πc 2 nи при n = 100 см−3:R ≈ 9 м.Ответ: а) j ≈ 6 ⋅ 1017 м −2 ⋅ с −1 ; б) R ≈ 9 м.11.3. Задачи для самостоятельного решенияЗадача 11.3.1. В спектре некоторой звезды максимуму излучения соответствует частота ≈1015 Гц. Найти температуру поверхности этого космического объекта.Ответ: ≈10 000 К.Задача 11.3.2. Найти температуру черного тела, если длинаволны, соответствующая максимуму его излучательной способности, на λ = 0,5 мкм больше, чем при температуре 2500 К.Ответ: ≈ 1750 К.Задача 11.3.3. При какой длине волны излучательная способность абсолютно черного тела с энергетической светимостью 3,0Вт/см2 максимальна?Ответ: 3,4 мкм.Задача 11.3.4.

Излучательная способность Солнца максимальнавблизи длины волны 0,48 мкм. В предположении, что Солнце излучает как абсолютно черное тело, оценить: 1) какую массу теряетСолнце ежесекундно за счет теплового излучения? и 2) за какоевремя масса Солнца должна уменьшаться на 1%?Ответ: 1) 0,5 1010 кг/с; 2) ≈1011 лет.Задача 11.3.5. Черный тонкостенный металлический сосуд,имеющий форму куба, заполнен водой, нагретой до 50°С.

Источник