Что больше ускорение сообщаемое землей солнцу или ускорение

Ускорение свободного падения на Земле

Что такое ускорение свободного падения на Земле ? На самом деле, это ускорение, которое придаёт телу силу тяжести, независимо от других воздействующих на него сил.
Понятие ускорения свободного падения используется в уравнении движения тел в неинерциальных системах отсчёта. То есть применяемых при движении с ускорением или системах отсчёта, поворачивающихся относительно инерциальной. При этом оно равняется силе тяжести, которая действует на тело.
Как установили, ускорение свободного падения нашей планеты ( g ) на экваторе приблизительно равно 9,78 м/с² , а на полюсах увеличивается до 9,82 м/с² . Хотя для точных расчетов принято использовать среднее или стандартное значение g=9,80665 м/с² . Также часто его значением указывают 9,8 или же округляют до 10 м/с² , но такие расчёты имеют лишь приблизительное значение.
К тому же, свободное падение на Земле можно выразить суммой двух ускорений. Если говорить точнее, то гравитационного ускорения, на которое влияет земное притяжение, и центростремительного ускорения, вызывающегося в результате вращения планеты вокруг своей оси.

Между прочим, ускорение свободного падения на Земле и других планетах может различаться. Всё дело в том, что на него влияют несколько факторов. Например, земельное значение зависит от широты, времени суток, атмосферного давления и т.д.
Поскольку на ускорение оказывает влияние центробежные силы и радиус тела, то свободное падение на экваторе Земли ниже, чем на полюсах.
Для того, чтобы рассчитать показатель силы ускорения у поверхности Земли необходимо обратиться к формуле:

Таким образом, мы получим приблизительно значение падения тел на Землю на определённой широте.

Теория Ньютона про ускорение свободного падения

Можно сказать, что это одно из открытий Исаака Ньютона. На основе опыта своих предшественников он создал свою теорию о всемирном тяготении.

Ранее Галилео Галилей проводил эксперименты с движением тел в полёте. Хотя считалось, чем меньше весит объект, тем медленнее он падает, и наоборот. Но Галилей установил, что падение тел различной массы одинаково. То есть независимо от массы тел, их приземление идентично. Правда, в экспериментах была небольшая неточность, которую Галилео списал на влияние сопротивления воздуха.
Помимо этого благодаря законам Кеплера, гелиоцентрической системе мира, а также накопленному опыту других учёных, Ньютон вычислил существование притяжения на Земле и в космосе.

Закон всемирного тяготения

Как известно, любой объект притягивается планетой или, проще говоря, тяготеет к её поверхности. Собственно, из-за этого закон так называется.
Формулировка закона звучит следующим образом: два материальных объекта притягиваются друг к другу с определённой силой. Величина такой силы прямо пропорциональна произведению массы данных объектов, а также обратно пропорциональна квадрату расстояния между ними.

Стоит отметить, что гравитационная постоянная (G), используемая в Международной системе единиц, равна 6,674 30(15)⋅10⁻¹¹ м³·кг⁻¹·с⁻² .

Кроме того, между всеми материальными телами действует сила взаимного притяжения. Такое явление называют гравитацией.

Платон мне друг, Аристотель мне друг, но самый большой мой друг – истина.Сэр Исаак Ньютон

Правда, закон Ньютона применим лишь для материальных объектов. То есть действуют в рамках классической механики. А вот взаимодействие (силу притяжения) на микроуровне можно определить следующим образом:

• если одно тело материально, а другое, например, однородный шар или сфера, тогда для расчёта используется масса тела и масса шара, а также расстояние между центрами этих масс.
• в случае, когда оба объекта являются однородными, используют их массы и расстояние между центрами данных масс.

Безусловно, Исаак Ньютон проделал огромнейшую работу, он определил и доказал принцип силы тяготения. Тем более, что его закон действителен при астрономических расчётах. Ведь на любое космическое тело действует сила тяжести.
Конечно, сейчас мы уже можем рассчитать ускорение свободного падения на планете, в том числе и на нашей Земле . Однако не стоит забывать, сколько трудов на протяжении сотен лет вложили многие учёные.

Источник

Ускорение земного падения

Ускоре́ние свобо́дного паде́ния g (обычно произносится как «Жэ» или «Жи»), — ускорение, сообщаемое телу под действием притяжения планеты или другого астрономического тела в безвоздушном пространстве — вакууме. Его значение для Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с², а в технических расчетах обычно принимают g = 9,81 м/с².

Значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.

Реальное ускорение свободного падения на поверхности Земли зависит от широты и варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах [1] . Оно может быть вычислено по эмпирической формуле:

g = 9,780327(1 + 0,0053024sin 2 (φ) − 0,0000058sin 2 (2φ)) ,

где φ — широта рассматриваемого места. [2]

Содержание

Вычисление ускорения свободного падения

Ускорение свободного падения состоит из двух слагаемых: гравитационного ускорения и центростремительного ускорения.

Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:

,

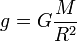
Если применить эту формулу для вычисления гравитационного ускорения на поверхности Земли, мы получим

м/с²

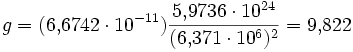
Полученное значение приблизительно совпадает с ускорением свободного падения. Отличия обусловлены:

• центростремительным ускорением в системе отсчёта, связанной с вращающейся Землёй;
• неточностью формулы из-за того, что масса планеты распределена по объёму, который, кроме того, имеет нешарообразную форму(см. геоид);
• неоднородностью Земли, что используется для поиска полезных ископаемых по гравитационным аномалиям;

Исторически масса Земли была впервые определена Генри Кавендишем, исходя из известного ускорения свободного падения и радиуса Земли, и впервые измеренной им гравитационной постоянной.

Перегрузки

Термин жэ используется в космонавтике и авиации для обозначения перегрузок — увеличения веса тела, вызванного его ускоренным движением. Допустимое значение перегрузок для гражданских самолетов составляет 4,33 жи. Обычный человек может выдерживать перегрузки до 5 g. Тренированные пилоты в антиперегрузочных костюмах могут переносить перегрузки до 9 g. Сопротивляемость к отрицательным, направленным вверх перегрузкам, значительно ниже. Обычно при 2-3 g в глазах «краснеет» и человек теряет сознание из-за прилива крови к голове.

В этом вопросе существует небольшая терминологическая путаница: к примеру, определение перегрузки выше даёт для стоящего неподвижно человека перегрузку в 0g, но в таблице ниже этот же случай рассматривается как перегрузка в 1g. Похожий казус происходит при измерении давления: мы говорим — давление 0, подразумевая давление в одну атмосферу вокруг нас, учёный скажет — давление 0, подразумевая полное отсутствие молекул в данном объёме.

Источник

Что больше ускорение сообщаемое землей солнцу или ускорение

Оценим величины лунных и солнечных гравитационных возмущений и их влияние на движение спутников.

На рис. 28 показано, как можно построить геометрически путем векторного вычитания возмущающие ускорения от Луны в некоторых точках круговой орбиты радиуса 100 000 км. Чтобы найти вектор возмущающего ускорения в точке А, нужно из вектора гравитационного ускорения сообщаемого в точке А Луной, вычесть вектор гравитационного ускорения сообщаемого Луной Земле. Как это делается, показано на том же рисунке. Так как гравитационное ускорение меньше по величине, чем

то возмущающее ускорение направлено к Луне. Но в точке В возмущающее ускорение направлено прямо от Луны, в точках почти к Земле, в точке почти по касательной. Максимальным будет возмущающее ускорение в точке А, где оно равно что составляет 0,052% от гравитационного ускорения, сообщаемого в этой точке Землей [2.11.

Рис. 28. Возмущающие ускорения от лунного притяжения.

С возмущающими ускорениями от Солнца дело обстоит так, как показано на рис. 29. Солнце находится столь далеко от Земли по сравнению со спутником, что можно считать векторы гравитационных ускорений во всех точках орбиты направленными параллельно. В точке А гравитационное ускорение максимально, в точке В — минимально, в точках гравитационные ускорения равны примерно полусумме ускорений в точках А и В и равны ускорению Земли. В результате возмущающие ускорения направлены на одной половине орбиты к Солнцу, на другой — от Солнца, причем в точках они будут максимальны или 0,024% местного земного гравитационного ускорения [2.1]), а в точках равны нулю (рис. 29).

При этом, чем ближе спутник к Земле, тем меньше возмущения по величине (из-за малой разницы между гравитационными ускорениями спутника и Земли от небесного тела) и в еще более высокой степени меньше та часть, которую они составляют от ускорения земного тяготения. До высоты лунные и

солнечные возмущения меньше возмущений от аномалий силы тяжести, которые обычно не учитываются даже при точных расчетах, выше превосходят их, оставаясь, однако, меньше возмущений от сплюснутости Земли, а выше превосходят и их.

Эффект влияния лунных и солнечных возмущений сильно зависит от формы орбиты и расположения ее плоскости и большой оси относительно направлений Земля — Луна и Земля — Солнце. Эти возмущения, естественно, не влияют, например, на положение плоскости орбиты, если указанные направления лежат в этой плоскости. Из того, что говорилось выше о солнечных возмущениях в точках (рис. 29), ясно, что действие Солнца вовсе не должно сказываться на орбите, плоскость которой перпендикулярна к направлению на Солнце. Но уже через 3 месяца вследствие движения Земли вокруг Солнца последнее окажется в плоскости орбиты, как на рис. 29, и солнечные возмущения в точках достигнут максимальных значений. Эффект их действия в этих точках, однако, будет ничтожен из-за того, что они будут направлены поперек орбитальной скорости. В других точках орбиты в этом смысле эффект должен был бы быть больше, но там сами возмущающие ускорения меньше. Максимальные эффекты лунных возмущений для круговой орбиты высотой за один оборот таковы: увеличение периода обращения на 290 с, уход вперед на боковое смещение спутника на поворот плоскости орбиты на Солнечные возмущения примерно в 2,2 раза меньше [2.11.

Рис. 29. Возмущающие ускорения от солнечного притяжения.

В целом круговые орбиты, даже очень большие, устойчивы против возмущений, если они слабо наклонены к плоскости эклиптики (или к плоскости орбиты Луны). Это ясно видно на примере орбит Луны и планет.

Совсем иначе обстоит дело с сильно вытянутыми эллиптическими орбитами, возмущения которых могут привести к полному разрушению орбиты.

Наиболее серьезно возмущения при этом сказываются на апогее орбиты, где возмущающее ускорение, во-первых, больше, чем в перигее, вследствие удаленности от Земли, во-вторых, по той же причине составляет большую долю от земного притяжения,

в-третьих, воздействует на сравнительно малую орбитальную скорость. При этом эффект в апогее будет значительным в том случае, если возмущающее ускорение окажется направленным не поперек апогейной скорости (как бывает при совпадении большой оси орбиты с линией Земля — Луна), а по ней или против нее.

Рис. 30. Лунные возмущения эллиптическим орбит.

На рис. 30 изображена примерная картина лунных возмущений для четырех по-разному расположенных одинаковых эллиптических орбит.

В апогеях эллипсов 1 и 2 возмущающие ускорения направлены против скорости, уменьшают ее и тем самым приводят к понижению перигеев. Напротив, в апогеях эллипсов 3 и 4 скорости увеличиваются, что вызывает повышение перигея. Интересно, что величина изменения высоты перигея зависит почти исключительно от высоты апогея и слабо связана с высотой перигея. При апогеях на высотах от до изменение высоты перигея за виток достигает нескольких километров и даже десятков километров (65,5 км для орбиты с перигеем на высоте 50 000 км и апогеем на высоте 100 000 км [2.1]).

Если повышение перигея не чревато опасностями для спутника, то понижение его с каждым оборотом в конце концов приведет ко входу спутника в земную атмосферу и гибели его. Для очень больших эллиптических орбит геометрическая картина окажется более сложной, а так как период обращения может стать близок к периоду обращения Луны вокруг Земли, то сильное воздействие на апогейную скорость будет случаться реже, но зато сама апогейная скорость станет так мала, что эффект каждого «удачного» возмущения будет весьма велик.

Судьба спутника с апогеем, находящимся за орбитой Луны, может быть различной. Совместное действие лунных и

солнечных возмущений может привести спутник к гибели в результате опускания перигея или, наоборот, вырвать его из сферы действия Земли и перевести на орбиту искусственной планеты.

С первым случаем космонавтика столкнулась на практике, когда советская станция «Луна-3» после облета Луны оказалась на орбите спутника Земли с апогеем на расстоянии от центра Земли и перигеем на расстоянии (период обращения 15 суток). Апогей с каждым оборотом повышался, но до границы сферы действия было далеко, и понижение перигея привело к гибели станции через полгода, после 11 оборотов.

Второй случай произошел со станцией «Луна-4», которая, пройдя вблизи Луны, оказалась на орбите спутника с апогеем и перигеем (период обращения примерно месяц). За период с апреля 1963 г. до конца года апогей орбиты достиг границы сферы действия Земли.

Источник