Радиус Шварцшильда
Гравитацио́нный ра́диус (или ра́диус Шва́рцшильда) в Общей теории относительности (ОТО) представляет собой характерный радиус, определённый для любого физического тела, обладающего массой: это радиус сферы, на которой находился бы горизонт событий, создаваемый этой массой, если бы она была распределена сферически-симметрично, была бы неподвижной (в частности, не вращалась), и целиком лежала бы внутри этой сферы.
По величине гравитационный радиус в ОТО совпадает с радиусом сферически-симметричного тела, для которого в классической механике вторая космическая скорость на поверхности была бы равна скорости света. На важность этой величины впервые обратил внимание Джон Мичелл в своём письме к Генри Кавендишу, опубликованном в 1784 году. В рамках ОТО гравитационный радиус впервые вычислил в 1916 году Карл Шварцшильд (см. метрика Шварцшильда).
Гравитационный радиус пропорционален массе тела m и равен rg = 2Gm / c 2 , где G — гравитационная постоянная, с — скорость света в вакууме. Это выражение можно записать как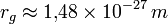 
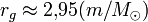
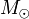
, где rg измеряется в метрах, а m — в килограммах. Для астрофизики удобной является запись 
км, где 
— масса Солнца.
Гравитационный радиус обычных астрофизических объектов ничтожно мал по сравнению с их действительным размером; так, для Земли rg = 8,84 мм, для Солнца rg = 2,95 км. Исключение составляют нейтронные звёзды и гипотетические кварковые звёзды. Например, для типичной нейтронной звезды радиус Шварцшильда составляет около 1/3 от её собственного радиуса. Это обусловливает важность эффектов ОТО при изучении таких объектов.
Если тело сжать до размеров гравитационного радиуса, то никакие силы не смогут остановить его дальнейшего сжатия под действием сил тяготения. Такой процесс, называемый релятивистским гравитационным коллапсом, может происходить с достаточно массивными звёздами (как показывает расчёт, с массой больше двух солнечных масс) в конце их эволюции: если, исчерпав ядерное «горючее», звезда не взрывается и не теряет массу, то, сжимаясь до размеров гравитационного радиуса, она должна испытывать релятивистский гравитационный коллапс. При гравитационном коллапсе из-под сферы радиуса rg не может выходить никакое излучение, никакие частицы. С точки зрения внешнего наблюдателя, находящегося далеко от звезды, с приближением размеров звезды к rg время неограниченно замедляет темп своего течения. Поэтому для такого наблюдателя радиус коллапсирующей звезды приближается к гравитационному радиусу асимптотически, никогда не становясь меньше его.
Физическое тело, испытавшее гравитационный коллапс, как и тело, радиус которого меньше его гравитационного радиуса, называется чёрной дырой. Сфера радиуса rg совпадает с горизонтом событий невращающейся чёрной дыры. Для вращающейся чёрной дыры горизонт событий имеет форму эллипсоида, и гравитационный радиус даёт оценку его размеров. Радиус Шварцшильда для сверхмассивной чёрной дыры в центре Галактики равен примерно 16 миллионам километров [1] . Радиус Шварцшильда сферы, равномерно заполненной веществом с плотностью, которая равна критической плотности, совпадает с радиусом наблюдаемой Вселенной.
См. также
Ссылки
- ↑Открыт объект у горизонта событий чёрной дыры Млечного Пути. «Мембрана (портал)» (4 сентября 2008). Проверено 12 декабря 2008.
Wikimedia Foundation . 2010 .
Смотреть что такое «Радиус Шварцшильда» в других словарях:
РАДИУС ШВАРЦШИЛЬДА — РАДИУС ШВАРЦШИЛЬДА, критический радиус, при котором массивное тело под влиянием своего собственного ПРИТЯЖЕНИЯ становится ЧЕРНОЙ ДЫРОЙ. Это радиус «ГОРИЗОНТА СОБЫТИЙ» черной дыры, из которого ничто не может вырваться, даже свет. Этот радиус… … Научно-технический энциклопедический словарь
ШВАРЦШИЛЬДА ПРОСТРАНСТВО-ВРЕМЯ — пространство время вне массивного невращающегося тела в вакууме (тензор Риччи Rik = 0). Элемент длины ds определяется выражением где r,q, f сферические координаты с центром в центре массивного тела, M масса тела. Это решение ур ний Эйнштейна… … Физическая энциклопедия
ШВАРЦШИЛЬДА МЕТРИКА — метрика четырехмерного псевдориманова пространства, к рая может быть приведена к виду где rg и с константы. Ш. м. состоит из двух связных компонент: первая из них (r>rg) наз. внешней Ш. м., вторая (r Математическая энциклопедия
Решение Шварцшильда — Общая теория относительности Математическая формулировка ОТО Космология Фундаментальные идеи Специальная теория относительности … Википедия
Метрика Шварцшильда — Общая теория относительности … Википедия
Гравитационный радиус — (или радиус Шварцшильда) представляет собой характерный радиус, определённый для любого физического тела, обладающего массой: это радиус сферы в яркостных координатах, на которой находился бы горизонт событий, создаваемый этой массой в общей… … Википедия
Пространство Шварцшильда — Общая теория относительности Математическая формулировка ОТО Космология Фундаментальные идеи Специальная теория относительности … Википедия
Чёрная дыра — У этого термина существуют и другие значения, см. Чёрная дыра (значения). Изображение, полученное с помощью телескопа «Хаббл»: Активная галактика M87. В ядре галактики, предположительно, находится чёрная дыра. На сни … Википедия
Квантовая чёрная дыра — Общая теория относительности Математическая формулировка ОТО Космология Фундаментальные идеи Специальная теория относительности … Википедия
Квантовые черные дыры — Общая теория относительности Математическая формулировка ОТО Космология Фундаментальные идеи Специальная теория относительности … Википедия
Источник
Радиус Шварцшильда
Радиус Шварцшильда (иногда называемый гравитационный радиус[1]) представляет собой характерный радиус, определенный для любого физического тела, обладающего массой. Для заданной массы, это радиус, до которого нужно стиснуть массу чтобы она сколлапсировала в гравитационную сингулярность. Этот термин используется в физике и астрономии, в особенности в теории гравитации и общей теории относительности. На важность этого понятия впервые обратил внимание в 1916 году Шварцшильд, который нашел точное решение уравнений общей теории относительности вокруг сферически-симметричной невращающейся массы (см. метрика Шварцшильда).
Радиус Шварцшильда для некоторого физического тела пропорционален его массе. Радиус Шварцшильда для тела с массой Земли равен 9 мм, для Солнца ≈ 3 км.
Физическое тело, радиус которого меньше его радиуса Шварцшильда, превращается в черную дыру. Поверхность сферы Шварцшильдовского радиуса представляет собой горизонт событий для невращающегося тела (для вращающейся черной дыры, горизонт событий имеет форму эллипсоида, и радиус Шварцшильда дает оценку размеров этого эллипсоида.) Радиус Шварцшильда для сверхмассивной черной дыры в центре нашей галактики равен примерно 7.8 миллионов км. Радиус Шварцшильда сферы, равномерно заполненной веществом с плотностью, которая равна критической плотности, совпадает с радиусом наблюдаемой Вселенной.
Формула радиуса Шварцшильда [ править | править код ]
Радиус Шварцшильда пропорционален массе, в коэффициент пропорциональности входит гравитационная постоянная и скорость света. Формула для радиуса Шварцшильда получается, если приравнять вторую космическую скорость скорости света:
.
— радиус Шварцшильда — гравитационная постоянная, равная 6.6742 × 10 -11 м 3 / кг * c 2 ; — масса объекта — скорость света в вакууме, равная 299 792 458 м/с
Коэффициент пропорциональности, , равен примерно 1.48 × 10 -27 m / kg, т.е. уравнение выше можно записать как:
где измеряется в метрах и в килограммах.
Таким образом, объект с фиксированной плотностью может быть достаточно большим, чтобы сколлапсировать внутри собственного радиуса Шварцшильда:
Заметим, что хотя этот результат и правильный, для его полного вывода требуется применять аппарат общей теории относительности. Скорее всего, то что классическая Ньютоновская физика дает правильный результат, всего лишь случайное совпадение. В то же время возможно, что это имеет более глубокие корни и может указывать на существование неизвестных симметрий в природе.
Источник
Радиус Шварцшильда — Schwarzschild radius
Радиус Шварцшильда (иногда исторически называют гравитационным радиусом ) является физическим параметром , который появляется в решении Шварцшильда для уравнений Эйнштейна , соответствующей радиусу , определяющего горизонт событий шварцшильдовской черной дыры . Это характерный радиус, связанный с любым количеством массы. Радиус Шварцшильда был назван в честь немецкого астронома Карла Шварцшильда , который рассчитал это точное решение для общей теории относительности в 1916 году.
Радиус Шварцшильда задается как
р s знак равно 2 грамм M c 2 , <\ displaystyle r_ = <\ frac <2GM>
СОДЕРЖАНИЕ
История
В 1916 году Карл Шварцшильд получил точное решение уравнений поля Эйнштейна для гравитационного поля вне невращающегося сферически-симметричного тела с массой (см. Метрику Шварцшильда ). Решение содержало члены вида и , которые становятся сингулярными при и соответственно. Это стало известно как радиус Шварцшильда . Физическое значение этих особенностей обсуждалось десятилетиями. Было обнаружено, что точка в точке является координатной сингулярностью, что означает, что она является артефактом конкретной системы координат, которая использовалась; в то время как тот, что находится в физическом состоянии, и не может быть удален. Радиус Шварцшильда, тем не менее, является физически значимой величиной, как отмечалось выше и ниже. M <\ displaystyle M> 1 — р s / р <\ displaystyle 1- 1 1 — р s / р <\ displaystyle <\ frac <1><1- р знак равно 0 <\ displaystyle r = 0> р знак равно р s <\ displaystyle r = r_ > р s <\ displaystyle r_ > р знак равно р s <\ displaystyle r = r_ > р знак равно 0 <\ displaystyle r = 0>
Это выражение ранее вычислялось с использованием механики Ньютона как радиус сферически симметричного тела, при котором убегающая скорость равнялась скорости света. Он был обнаружен в 18 веке Джоном Мичеллом и Пьером-Симоном Лапласом .
Параметры
Радиус Шварцшильда объекта пропорционален массе. Соответственно, у Солнца есть радиус Шварцшильда приблизительно 3,0 км (1,9 мили), тогда как у Земли всего около 9 мм (0,35 дюйма ), а у Луны — около 0,1 мм (0,0039 дюйма). Масса наблюдаемой Вселенной имеет радиус Шварцшильда приблизительно 13,7 миллиарда световых лет.
| Объект | Масса, M <\ textstyle M> | Радиус Шварцшильда, 2 грамм M c 2 <\ textstyle <\ frac <2GM> | Фактический радиус, р <\ textstyle r> | Плотность Шварцшильда, или 3 c 6 32 π грамм 3 M 2 <\ textstyle <\ frac <3c ^ <6>> <32 \ pi G ^ <3>M ^ <2>>>> 3 c 2 8 π грамм р 2 <\ textstyle <\ frac <3c ^ <2>> <8 \ pi Gr ^ <2>>>> |
|---|---|---|---|---|
| Наблюдаемая Вселенная | 8,8 × 10 52 кг | 1,3 × 10 26 м (13,7 млрд св. Лет ) | 4,4 × 10 26 м (46,5 млрд св. Лет ) | 9,5 × 10 — 27 кг / м 3 |
| Млечный Путь | 1,6 × 10 42 кг | 2,4 × 10 15 м (0,25 св. Лет ) | 5 × 10 20 м (52,9 тыс. Св. Лет ) | 0,000029 кг / м 3 |
| TON 618 (самая большая из известных черных дыр ) | 1,3 × 10 41 кг | 1,9 × 10 14 м ( 1300 а.е. ) | 0,0045 кг / м 3 | |
| SMBH в NGC 4889 | 4,2 × 10 40 кг | 6,2 × 10 13 м | 0,042 кг / м 3 | |
| SMBH в Мессье 87 | 1,3 × 10 40 кг | 1,9 × 10 13 м | 0,44 кг / м 3 | |
| СМЧД в галактике Андромеды | 3,4 × 10 38 кг | 5,0 × 10 11 м | 640 кг / м 3 | |
| Стрелец А * (SMBH в Млечном Пути) | 8,2 × 10 36 кг | 1,2 × 10 10 м | 1,1 × 10 6 кг / м 3 | |
| солнце | 1,99 × 10 30 кг | 2,95 × 10 3 м | 7,0 × 10 8 м | 1,84 × 10 19 кг / м 3 |
| Юпитер | 1,90 × 10 27 кг | 2,82 м | 7,0 × 10 7 м | 2,02 × 10 25 кг / м 3 |
| земля | 5,97 × 10 24 кг | 8,87 × 10 — 3 м | 6.37 × 10 6 м | 2,04 × 10 30 кг / м 3 |
| Луна | 7,35 × 10 22 кг | 1,09 × 10 — 4 м | 1,74 × 10 6 м | 1,35 × 10 34 кг / м 3 |
| Сатурн | 5,683 × 10 26 кг | 8,42 × 10 — 1 м | 6,03 × 10 7 м | 2,27 × 10 26 кг / м 3 |
| Уран | 8,681 × 10 25 кг | 1,29 × 10 — 1 м | 2,56 × 10 7 м | 9,68 × 10 27 кг / м 3 |
| Нептун | 1.024 × 10 26 кг | 1,52 × 10 — 1 м | 2,47 × 10 7 м | 6,97 × 10 27 кг / м 3 |
| Меркурий | 3,285 × 10 23 кг | 4,87 × 10 — 4 м | 2,44 × 10 6 м | 6,79 × 10 32 кг / м 3 |
| Венера | 4,867 × 10 24 кг | 7,21 × 10 — 3 м | 6,05 × 10 6 м | 3,10 × 10 30 кг / м 3 |
| Марс | 6,39 × 10 23 кг | 9,47 × 10 — 4 м | 3,39 × 10 6 м | 1,80 × 10 32 кг / м 3 |
| Человек | 70 кг | 1,04 × 10 — 25 м | 1,49 × 10 76 кг / м 3 | |
| Планковская масса | 2,18 × 10 — 8 кг | 3,23 × 10 — 35 м | (вдвое больше планковской длины ) | 1,54 × 10 95 кг / м 3 |
Вывод
Классификация черных дыр по радиусу Шварцшильда
| Класс | Прибл. масса | Прибл. радиус |
|---|---|---|
| Сверхмассивная черная дыра | 10 5 –10 10 м вс | 0,001–400 а.е. |
| Черная дыра средней массы | 10 3 Пн вс | 10 3 км ≈ R Земля |
| Звездная черная дыра | 10 Пн вс | 30 км |
| Микро черная дыра | до M Moon | до 0,1 мм |
Любой объект, радиус которого меньше его радиуса Шварцшильда, называется черной дырой . Поверхность в радиусе Шварцшильда действует как горизонт событий в невращающемся теле ( вращающаяся черная дыра действует несколько иначе). Ни свет, ни частицы не могут выйти через эту поверхность из области внутри, отсюда и название «черная дыра».
Черные дыры можно классифицировать на основе их радиуса Шварцшильда или, что эквивалентно, по их плотности, где плотность определяется как масса черной дыры, деленная на объем ее сферы Шварцшильда. Поскольку радиус Шварцшильда линейно связан с массой, а замкнутый объем соответствует третьей степени радиуса, поэтому маленькие черные дыры намного плотнее больших. Объем, заключенный в горизонте событий наиболее массивных черных дыр, имеет среднюю плотность ниже, чем у звезд главной последовательности.
Сверхмассивная черная дыра
Сверхмассивная черная дыра (SMBH) является крупнейшим типа черной дыры, хотя есть несколько официальных критериев относительно того, как такой объект считается так, порядка сотен тысяч до миллиардов солнечных масс. ( Были обнаружены сверхмассивные черные дыры размером до 21 миллиарда (2,1 × 10 10 ) M ☉ , такие как NGC 4889 ). В отличие от черных дыр звездной массы , сверхмассивные черные дыры имеют сравнительно низкую среднюю плотность. (Обратите внимание, что (невращающаяся) черная дыра — это сферическая область в пространстве, которая окружает сингулярность в ее центре; это не сама сингулярность.) С учетом этого средняя плотность сверхмассивной черной дыры может быть меньше, чем плотность воды.
Радиус Шварцшильда тела пропорционален его массе и, следовательно, его объему, если предположить, что тело имеет постоянную плотность массы. Напротив, физический радиус тела пропорционален кубическому корню из его объема. Следовательно, поскольку тело накапливает материю с заданной фиксированной плотностью (в данном примере 997 кг / м 3 , плотность воды), его радиус Шварцшильда будет увеличиваться быстрее, чем его физический радиус. Когда тело такой плотности вырастет до примерно 136 миллионов солнечных масс (1,36 × 10 8 ) M ☉ , его физический радиус превзойдет его радиус Шварцшильда, и, таким образом, оно образует сверхмассивную черную дыру.
Считается, что подобные сверхмассивные черные дыры не образуются сразу в результате сингулярного коллапса звездного скопления. Вместо этого они могут начать жизнь в виде меньших черных дыр звездных размеров и расти за счет аккреции материи или даже других черных дыр.
Радиус Шварцшильда сверхмассивной черной дыры в Центре Галактики составляет примерно 12 миллионов километров.
Звездная черная дыра
Звездные черные дыры имеют гораздо большую среднюю плотность, чем сверхмассивные черные дыры. Если накапливать вещество с ядерной плотностью (плотность ядра атома около 10 18 кг / м 3 ; нейтронные звезды также достигают этой плотности), такое накопление будет находиться в пределах его собственного радиуса Шварцшильда около 3 M ☉ и, следовательно, будет звездной черной дырой .
Изначальная черная дыра
Небольшая масса имеет чрезвычайно малый радиус Шварцшильда. Масса, подобная Эвересту, имеет радиус Шварцшильда намного меньше нанометра . Его средняя плотность при таком размере будет настолько высока, что ни один известный механизм не сможет формировать такие чрезвычайно компактные объекты. Такие черные дыры могли образоваться на ранней стадии эволюции Вселенной, сразу после Большого взрыва , когда плотности были чрезвычайно высоки. Поэтому эти гипотетические миниатюрные черные дыры называют первичными черными дырами .
Другое использование
В гравитационном замедлении времени
Гравитационное замедление времени вблизи большого, медленно вращающегося, почти сферического тела, такого как Земля или Солнце, может быть разумно следующим:
т р т знак равно 1 — р s р <\ displaystyle <\ frac
t r — время, прошедшее для наблюдателя при радиальной координате r в гравитационном поле; t — время, прошедшее для наблюдателя, удаленного от массивного объекта (и, следовательно, вне гравитационного поля); r — радиальная координата наблюдателя (аналогична классическому расстоянию от центра объекта); r s — радиус Шварцшильда.
Радиус Шварцшильда для массы Планка
Для массы Планка радиус Шварцшильда и длина волны Комптона того же порядка, что и длина Планка . м п знак равно ℏ c / грамм <\ Displaystyle м _ <\ rm
> = <\ sqrt <\ hbar c / G>>> р S знак равно 2 ℓ п <\ Displaystyle г _ <\ rm > = 2 \ ell _ <\ rm
>> >> > = <\ sqrt <\ hbar G / c ^ <3>>>> Классификация черных дыр по типу: Классификация черных дыр по массе: Источникλ C знак равно 2 π ℓ п <\ displaystyle \ lambda _ <\ rm ℓ п знак равно ℏ грамм / c 3 <\ displaystyle \ ell _ <\ rm Смотрите также