[вещества]Наша Вселенная и рекурсия
К примеру, ставим какой-то предмет между двумя зеркалами, получаем бесконечную рекурсию. Или подключаем видеокамеру к телевизору, включаем, направляем на телевизор. Опять бесконечная рекурсия. Однако ни тормозов, ни падения Вселенной не заметно. Как такое возможно? Или там какой-то грязный хак?
Re: [вещества]Наша Вселенная и рекурсия
Держи! Сегодня читал и плакал от счастья!
P.S. в том случае рекурсия ни разу не бесконечна — начиная от поглощения в зеркалах и кончая дискретностью потка световой энергии.
Re: [вещества]Наша Вселенная и рекурсия
в том имеется в виду в твоём а документ прочти прям щас — обосрёшься кирпичами.
Re: [вещества]Наша Вселенная и рекурсия
отпишись когда прочтёшь, я тут пока кино про стрейнджлава смотрю.
Re: [вещества]Наша Вселенная и рекурсия
>>К примеру, ставим какой-то предмет между двумя зеркалами, получаем бесконечную рекурсию. Или подключаем видеокамеру к телевизору, включаем, направляем на телевизор. Опять бесконечная рекурсия. Однако ни тормозов, ни падения Вселенной не заметно. Как такое возможно? Или там какой-то грязный хак?
учи мат. часть. это не рекурсия а банальная обратная связь.
Re: [вещества]Наша Вселенная и рекурсия
>учи мат. часть. это не рекурсия а банальная обратная связь.
самовозбуждение называется. известно из пионэрского радиокружка.
Re: [вещества]Наша Вселенная и рекурсия
процесс не бесконечен, а вычислительные мощности велики. кури физику.
Re: [вещества]Наша Вселенная и рекурсия
Re: [вещества]Наша Вселенная и рекурсия
>Или там какой-то грязный хак?
Ага, называется «скорость света»
Re: [вещества]Наша Вселенная и рекурсия
Re: [вещества]Наша Вселенная и рекурсия
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.
Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.
Re: [вещества]Наша Вселенная и рекурсия
Re: [вещества]Наша Вселенная и рекурсия
> Как такое возможно? Или там какой-то грязный хак?
Re: [вещества]Наша Вселенная и рекурсия
Вселеная замкнутая, если пукнуть нерассеивающейся струей идеального газа, то со временем струя вернется с другой стороны — это закон круговорота метана в природе.
Источник
Рекурсия вокруг нас: люди, соборы и капуста романеско
Спойлер: рекурсия есть не только в цифровом мире. Встречается она и в реальном. И намного чаще, чем вы думаете, — разная и интересная.
Про рекурсивные функции я узнала на уроках информатики. Потом долго считала рекурсию всего лишь отвлечённым понятием из программирования, далёким от реальной жизни. Почему-то в школе нам не рассказывают, что на самом деле явление это встречается в природе, науке, искусстве, а рекурсивные алгоритмы применимы даже для решения бытовых задач.
Что такое рекурсия
В программировании рекурсивная функция — это такая функция, которая вызывает себя из себя же самой, но с другими значениями параметров.
Примечание. Функция может вызывать себя и через промежуточные функции. Например, функция А запускает функцию Б, а та снова вызывает А.
Цепочка вызовов не может быть бесконечной, она должна прерваться и выдать ответ. Поэтому должен возникать крайний случай (или несколько), когда функции уже не нужно вызывать себя с другими параметрами (то есть погружаться ещё глубже), а можно сразу вернуть результат.
Звучит и правда сложно, но не пугайтесь — с примером станет понятнее.
Классический пример рекурсивной функции — вычисление факториала, то есть произведения натуральных чисел от 1 до N.
Здесь N=0 — это крайний случай: функция ничего не вызывает и сразу возвращает единицу (по определению, факториал нуля равен единице).
В более широком смысле рекурсией называют описание или изображение предмета, объекта, явления внутри самого себя. Рекурсивный принцип — это принцип самовоспроизведения и одновременно усложнения системы по одному и тому же алгоритму.
Тут-то и выясняется, что и нас, людей, тоже можно считать рекурсивными: ведь в клетке заложена информация обо всём организме, в ДНК записана информация о том, как синтезировать ДНК.
Фулстек-разработчик. Любимый стек: Java + Angular, но в хорошей компании готова писать хоть на языке Ада.
Рекурсия — не то же самое, что бесконечный цикл
Хотя её часто с ним путают. Понять разницу проще всего на примере. Предположим, ваш начальник издал приказ:
Это не рекурсия. Просто в ситуации, когда начальник не прав, мы попадём в бесконечный цикл вызовов.
Но можно внести небольшое изменение и получить рекурсию:
Приказ стал рекурсивным, потому что в одной из веток вызывает сам себя.
На обед у нас салат «Рекурсивный»: помидоры, огурцы, салат.
Рекурсию можно увидеть
И это очень красиво. Рекурсивные изображения, они же фрактальные паттерны или просто фракталы, — это рисунки или предметы, которые подобны сами себе: состоят из уменьшенных копий себя.
В природе мы встречаемся с ними, рассматривая кроны деревьев: рисунок более крупных веток повторяется в узоре более мелких. И даже черешок листовой пластинки напоминает ствол дерева, а прилистники — его ветви.
Подобным же образом выстроены кровеносные сосуды и нервы в организме животных. Свойствами фракталов обладают снежинки, а ещё — удивительная капуста романеско. Вот она на картинке ниже — ну разве не красавица? 😀
В архитектуре рекурсия встречается в облике готических соборов.
В этом соборе XIII века задействован один из характерных для готики приёмов: его окна украшены тонкими ажурными перегородками. Их основной узор — стрельчатая арка с кругом внутри, круг поддерживается двумя арками меньшего размера.
А вот рекурсивная версия того же узора — Собор Линкольна.
Здесь окно тоже выполнено в форме остроконечной арки с вписанным в неё кругом, а круг лежит на двух других арках. Вот только внутри каждой из этих арок — снова круг и две ещё меньших арки, а внутри них — ещё по одному кругу на двух меньших арках.
Другой пример архитектурной рекурсии — собор Святого Петра в Ватикане.
Джордж Херси, американский писатель и журналист, сравнивал его с китайскими шкатулками с секретом. По его словам, архитектурный комплекс состоит из одной макроцеркви, четырёх наборов того, что журналист назвал макси-церквями, 16 мини-церквей и 32 микроцерквей. А мог бы просто сказать, что собор рекурсивный.
В изобразительном искусстве рекурсия тоже отметилась — взять хотя бы «Триптих Стефанески» Джотто. На его центральной панели изображён кардинал Стефанески, которой держит в руках этот же триптих (на котором тоже изображён триптих и так далее).
А вот пример посвежее — литография «Рисующие руки» нидерландского художника XX века Маурица Эшера:
Чтобы увидеть рекурсию, необязательно идти в картинную галерею — просто посмотрите на герб России. Двуглавый орёл держит в правой лапе скипетр, который увенчан двуглавым орлом, а тот тоже держит скипетр, который… 🙂 В общем — вот:
Рекурсию можно услышать
В музыке есть композиции, которые тоже можно назвать рекурсивными. Американский физик и писатель Дуглас Хофштадтер в своей книге «Гёдель, Эшер, Бах: эта бесконечная гирлянда» рассказывает о рекурсии, приводя в пример джигу из «Французской сюиты №5» Баха.
В первой её части трижды повторяется мелодический переход из тональности соль мажор в ре минор: мелодия как бы вызывает сама себя, погружаясь всё глубже. А во второй части, наоборот, трижды поднимается от ре к соль.
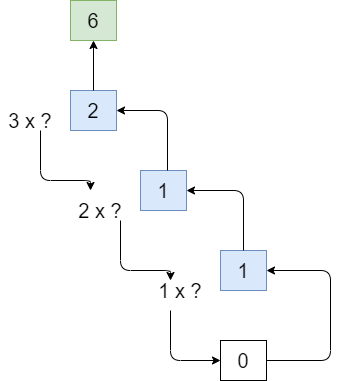
Программисту это может напомнить вычисление факториала числа 3: функция трижды вызывает саму себя, затем трижды возвращается с промежуточными результатами вычислений, а затем — с итоговым.
В лингвистике рекурсией называют способность языка порождать вложенные предложения и конструкции. Например, предложение «Саша читает статью про рекурсию» можно достроить до «Лена смотрит, как Саша читает статью про рекурсию». А его, в свою очередь, превратить в «Ленин друг Петя не одобряет, что Лена смотрит, как Саша читает статью про рекурсию».
Принято считать, что рекурсия свойственна любому человеческому языку (сомнения пока есть только насчёт языка пираха, на котором разговаривают в бразильской части бассейна Амазонки), а распознавать и понимать её — едва ли не врождённая способность людей.
Чтобы доказать это, немецкие учёные даже ставили эксперименты на пятимесячных младенцах. Они измеряли активность головного мозга с помощью ЭЭГ — и сравнивали реакцию малышей на вложенные языковые конструкции, правильные и неправильные. Так как дети были настолько малы, что речь ещё не понимали, вместо слов им проигрывали последовательности звуков разной частоты. Причём частоты звука для связанных слов во вложенных конструкциях совпадали.
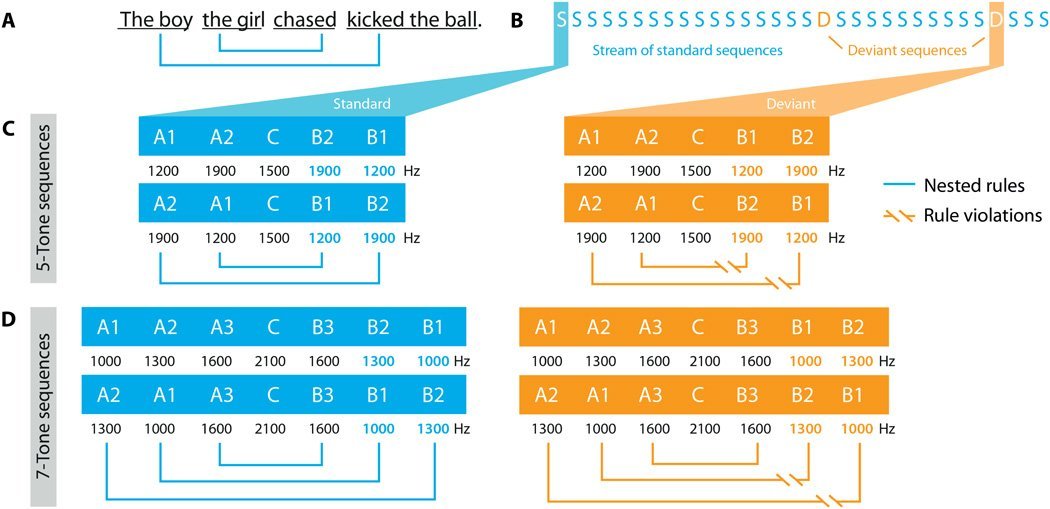
В предложении «Мальчик, за которым гналась девочка, пнул мяч» две связанные конструкции: 1) «мальчик пнул» и 2) «девочка гналась». Их обозначили звуками частотой 1900 и 1200 Герц и разделили коротким звуком в 1500 Герц. Слева — корректные, а справа — некорректные языковые паттерны. Кроме пятитоновых, проигрывались и семитоновые вложенные последовательности.
Научные подробности ищите в оригинальной публикации. Нам важнее выводы: эксперименты показали, что даже мозгу младенцев неправильные конструкции определённо не понравились.
Конечно, выборка (38 участников) слишком мала, чтобы распространять результаты на всё человечество, но теория интересная.
Рекурсивные алгоритмы легко смоделировать с помощью подручных средств
Возьмите, например, матрёшку. Все вложенные в неё куклы подобны кукле-шкатулке, кроме наименьшей, которая представляет собой базовый случай. То есть матрёшка — твёрдое воплощение рекурсии.
А если задаться целью поставить синюю точку на самой маленькой кукле, то можно буквально на пальцах реализовать рекурсивный алгоритм:
А вот алгоритм, для исполнения которого не нужны дополнительные предметы. Представьте, что вы сидите в последнем ряду длинного зала и хотите узнать, сколько всего в нём рядов. Конечно, можно встать и пересчитать их, но вам лень, а ещё вы уже знаете про рекурсию.
Так что вы спрашиваете соседа спереди, сколько перед ним рядов. Если он называет какое-то число, вы прибавляете к нему ещё два (один ряд — для соседа и один — тот, в котором сами сидите) и получаете ответ, а иначе — предлагаете этому самому соседу применить ваш гениальный алгоритм уже к его соседу спереди.
Если все участники процесса будут настроены доброжелательно, то в итоге очередь отвечать дойдёт до первого ряда и вам обратно по цепочке вернут результат — полученный с помощью рекурсивного алгоритма, между прочим. То есть:
- Маша, которая сидит в первом ряду, ответит Саше, сидящему за ней, что впереди неё рядов нет.
- Саша сложит ноль и один и ответит своему соседу сзади Пете, что впереди него (Саши) один ряд.
- Петя прибавит ещё единицу и ответит соседке Оле, что перед ним два ряда.
- И так далее…
- Сидящий перед вами Виталик скажет, что перед ним N рядов, а значит, сам он сидит в (N + 1)-м ряду и всего их в зале N + 2.
И минутка предметного юмора
— Помнишь, Антоха желание проиграл? Так вот, я ему загадал, чтобы он два дня на все предметы, с которыми что-то сделал, клеил стикер с названием этого действия.
— И что, он на каждый новый стикер клеил другой с надписью «наклеил»?
Подытожим
Рекурсивные предметы и явления окружают нас повсюду. Рекурсию можно увидеть, услышать, потрогать руками. Рекурсия — это просто. Чтобы понять её, не обязательно разбираться с фракталами или фугами Баха. Объяснить рекурсию можно даже пятилетнему ребёнку. Просто прочтите ему стишок Андрея Усачёва:
Шёл по улице жучок
В модном пиджачке.
На груди блестел значок,
А на том значке
Нарисован был жучок,
Тоже в пиджачке.
И на нём висел значок,
А на том значке
Был ещё один жучок…
Но он был так мал,
Что глядел я целый час
Был ли у жучка значок?
Был ли на значке жучок?
обложка: Валентина Палатурян для Skillbox
Источник