Квадратурная амплитудная модуляция (QAM): что это такое и где применяется
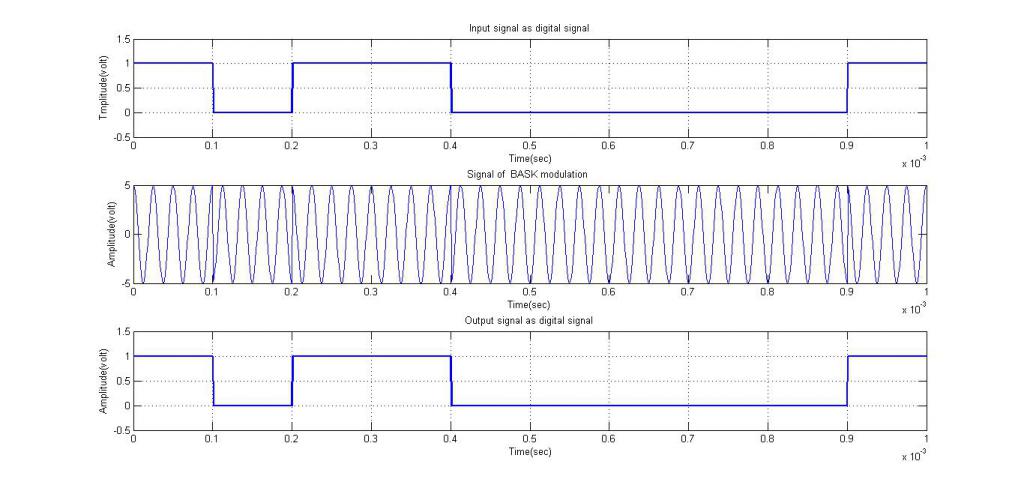
Модуляция QAM передает два аналоговых сигнала сообщений или два цифровых битовых потока путем изменения (модуляции) амплитуд двух несущих волн с использованием схемы цифровой модуляции с амплитудной манипуляцией (ASK) или аналоговой AM.
Принцип работы
Две несущие волны одной и той же частоты, обычно синусоиды, находятся вне фазы друг с другом на 90° и, таким образом, называются квадратурными несущими или квадратурными компонентами — отсюда и название схемы. Модулированные волны суммируются, а окончательная форма волны представляет собой комбинацию как фазовой манипуляции (PSK), так и амплитудной манипуляции (ASK), или в аналоговом случае фазовой модуляции (PM) и амплитудной модуляции.
Как и все схемы модуляции, QAM передает данные путем изменения какого-либо аспекта сигнала несущей волны (обычно синусоиды) в ответ на сигнал данных. В случае цифрового QAM используются несколько дискретных значений фазового и множественного дискретных значений амплитуды. Фазовая манипуляция (PSK) — это более простая форма QAM, в которой амплитуда несущей постоянна и сдвигается только фаза.
В случае основы передачи QAM, несущая волна является совокупностью двух синусоидальных волн с одинаковой частотой, 90° по фазе друг от друга (в квадратуре). Они часто называются «I» или синфазной составляющей, а также «Q» или квадратурной составляющей. Каждая волна компонента модулируется по амплитуде, то есть ее амплитуда изменяется для представления данных, которые должны быть перенесены до того, как они будут объединены вместе.
Применение
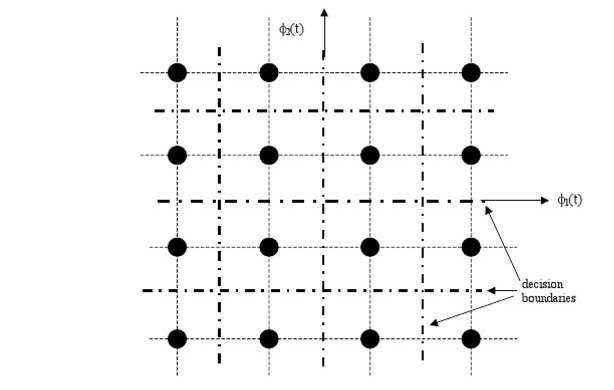
Надпись decision boundaries на фото выше обозначает границу поверхности (или «границу принятия решений», дословно).
QAM (quadrature amplitude modulation) широко используется в качестве схемы модуляции для цифровых телекоммуникационных систем таких, как стандарты 802.11 Wi-Fi. Произвольная высокая спектральная эффективность может быть достигнута с помощью QAM путем установки подходящего размера созвездия, ограниченного только уровнем шума и линейностью канала связи.
Модуляция QAM используется в системах с оптическим волокном по мере увеличения скорости передачи битов. QAM16 и QAM64 могут быть оптически эмулированы с 3-канальным интерферометром.
Цифровая техника
В цифровой QAM каждая составляющая волна состоит из выборок постоянной амплитуды, каждая из которых занимает единый временной интервал, а амплитуда квантуется, ограничивается одним из конечного числа уровней, представляющим одну или несколько двоичных цифр (бит) цифровой бит. В аналоговой QAM амплитуда каждой составляющей синусоидальной волны непрерывно изменяется во времени аналоговым сигналом.
Фазовую модуляция (аналоговый PM) и манипуляцию (цифровая PSK) можно рассматривать как частный случай QAM, где величина модулирующего сигнала является постоянной, причем только фаза изменяется. Квадратурную модуляцию также можно расширить до частотной модуляции (FM) и манипуляции (FSK), поскольку они могут рассматриваться как ее подвид.
Как и во многих схемах цифровой модуляции, диаграмма созвездия полезна для QAM. В QAM точки созвездия обычно расположены в квадратной сетке с равным вертикальным и горизонтальным расстоянием, хотя возможны и другие конфигурации (например, Cross-QAM). Поскольку в цифровой телекоммуникации данные обычно двоичные, количество точек в сетке обычно составляет 2 (2, 4, 8, . ).
Поскольку QAM обычно является квадратным, некоторые из них редки — наиболее распространенными формами являются 16-QAM, 64-QAM и 256-QAM. Перемещаясь в более созвездие более высокого порядка, можно передавать больше бит на символ. Однако, если средняя энергия созвездия остается неизменной (путем проведения справедливого сравнения), точки должны быть ближе друг к другу и, следовательно, более восприимчивы к шуму и другой коррупции.
Это приводит к более высокой частоте ошибок в битах, и поэтому QAM более высокого порядка может предоставлять больше данных менее надежно, чем QAM более низкого порядка, для постоянной средней энергии созвездия. Использование QAM более высокого порядка без увеличения скорости битовых ошибок требует более высокого отношения сигнал / шум (SNR) за счет увеличения энергии сигнала, уменьшения шума или того и другого.
Технические приспособления
Если требуются скорости передачи данных, превышающие тарифы, предлагаемые 8-PSK, более обычным является переход в QAM, поскольку он достигает большего расстояния между соседними точками в плоскости I-Q, распределяя точки более равномерно. Усложняющим фактором является то, что точки больше не имеют одинаковой амплитуды, и поэтому демодулятор должен теперь правильно определять как фазу, так и амплитуду, а не просто фазу.
Телевидение
64-QAM и 256-QAM часто используются в цифровом кабельном телевидении и кабельных модемах. В Соединенных Штатах 64-QAM и 256-QAM являются санкционированными схемами модуляции для цифрового кабеля, которые стандартизованы SCTE в стандартном ANSI / SCTE 07 2013. Обратите внимание, что многие специалисты по маркетингу будут ссылаться на них как на QAM-64 и QAM-256. Великобритании модуляция QAM-64 используется для цифрового наземного телевидения (Freeview), а 256-QAM используется для Freeview-HD.
Системы связи, предназначенные для достижения очень высоких уровней спектральной эффективности, обычно используют очень плотные частоты из этой серии. Например, в современных устройствах Ethernet Powerplug AV2 500-Mbit используются устройства 1024-QAM и 4096-QAM, а также будущие устройства, использующие стандарт ITU-T G.hn для подключения к существующей домашней проводке (коаксиальный кабель, телефонные линии и линии электропередач); 4096-QAM обеспечивает 12 бит / символ.
Другим примером является технология ADSL для медных витых пар, размер созвездия которых достигает 32768-QAM (в терминологии ADSL это называется битовой загрузкой или бит на тон, 32768-QAM эквивалентно 15 бит на тон).
Системы сверхвысокой пропускной способности с обратной связью также используют 1024-QAM. При использовании 1024-QAM, адаптивного кодирования и модуляции (ACM) и XPIC, производители могут получить гигабитную емкость в одном канале с частотой 56 МГц.
В SDR-приемнике
Известно, что круговая частота 8-QAM является оптимальной модуляцией 8-QAM в смысле необходимости наименьшей средней мощности для данного минимального евклидова расстояния. Частота 16-QAM является субоптимальной, хотя оптимальная может быть создана по тем же принципам, что и 8-QAM. Эти частоты часто используются при настройке SDR-приемника. Другие частоты могут быть воссозданы путем манипуляций с аналогичными (или похожими) частотами. Эти качества активно используются в современных СДР-приемниках и трансиверах, маршрутизаторах, роутерах.
Источник
Квадратурная модуляция (QAM)
Для увеличения скорости передачи данных используют так называемую квадратурную амплитудную модуляцию QAM, которая является амплитудно-фазовым видом модуляции. QAM применяется в кабельных модемах, в стандарте цифрового телевидения DVB-C, а также, в цифровом радиовещании СВЧ диапазона.
С точки зрения скорости передачи этот вид модуляции намного более эффективен по сравнению с двоичной (BPSK), четырехпозиционной (QPSK) или восьмипозиционной (8-PSK) фазовой модуляцией. Следует сразу оговориться, что QPSK и 4-QAM на самом деле один и тот же вид модуляции.
В 16-позиционной QAM (16-QAM) существует по четыре сигнальных значения для каждой из квадратурных компонент I и Q. Этим достигаются шестнадцать значений суммарного сигнала.
Зная, что , получаем, что в 16-QAM одним символом могут быть переданы четыре бита. Это означает, что символьная скорость в таком виде модуляции получается в четыре раза меньше битовой, т. е. равна 1/4 от битовой скорости. Таким образом, данный тип модуляции позволяет организовать спектрально более эффективную передачу данных. Векторная диаграмма сигнала 16-QAM приведена на рисунке 1.
Рисунок 1. Векторная диаграмма сигнала 16-QAM
Точно так же, как и в других системах модуляции в 16-QAM применяется кодирование Грея. Соответствие сигнальных созвездий, кода Грея и цифровых значений сигналов I и Q для 16-QAM, приведено на рисунке 2.
Рисунок 2. Соответствие сигнальных созвездий, кода Грея и цифровых значений сигналов I и Q для 16-QAM
Глазковая диаграмма сигналов I и Q для 16-позиционной квадратурной модуляции 16 QAM приведена на рисунке 3.
Рисунок 3. Глазковая диаграмма сигналов I и Q 16-позиционной квадратурной модуляции 16 QAM
В 16-ти позиционной QAM (16-QAM) существует по четыре сигнальных значения для каждой из квадратурных компонент I и Q. Этим достигаются 16 значений суммарного сигнала.
Для иллюстрации, на рисунке 4 приведена фотография экрана измерительного прибора — векторного анализатора. На этом рисунке видны векторная, глазковая диаграмма и основные характеристики сигнала 16-QAM на частоте 450 МГц.
Рисунок 4. Экран векторного анализатора, на котором видны векторная, глазковая диаграмма и основные характеристики сигнала 16-QAM на частоте 450 МГц
Еще одна разновидность QAM — это 32-QAM. Ее характеристики таковы: по шесть сигнальных значений для I и для Q, что в итоге дает точек созвездия для суммарного сигнала. Сигнальное созвездие сигнала 32-QAM приведено на рисунке 5.
Рисунок 5. Сигнальное созвездие сигнала 32-QAM
Этот тип модуляции наделен особенностью. В итоге, количество значений 36 не соответствует исходным данным, т.к. слишком велико, (). Поэтому, четыре «угловых» сигнальных значения, (на которые приходится большинство мощности передатчика), опущены. Этим уменьшается значение выходной мощности, которую должен генерировать передатчик. Исходя из того, что , получаем битовую скорость, равную 5 бит/с и символьную скорость, равную 1/5.
Особенность сигналов QAM — это возможность увеличивать количество сигнальных точек в обмен на помехоустойчивость. В результате в одной и той же полосе сигналов есть возможность увеличивать скорость передачи цифровой информации. Ограничение на увеличение пропускной способности канала накладывает только сложность реализации аппаратуры телекоммуникационных устройств
Дата последнего обновления файла 31.01.2020
Понравился материал? Поделись с друзьями!
- Steve C. Cripps RF Power Amplifiers for Wireless Communications — ARTECH HOUSE, INC., 2006
- Marian K. Kazimierczuk RF Power Amplifiers — John Wiley & Sons, Ltd 2008
- Радиопередающие устройства: учебник для ВУЗов; под ред. В. В. Шахгильдяна. — 3-е изд., перераб. и доп. — М.: Радио и связь, 2003.
Вместе со статьей «Квадратурная модуляция (QAM)» читают:
MSK-модуляция частотная с минимальным сдвигом по частоте
https://digteh.ru/UGFSvSPS/modul/MSK/
Автор Микушин А. В. All rights reserved. 2001 . 2020
Предыдущие версии сайта:
http://neic.nsk.su/
Об авторе:
к.т.н., доц., Александр Владимирович Микушин
Кандидат технических наук, доцент кафедры САПР СибГУТИ. Выпускник факультета радиосвязи и радиовещания (1982) Новосибирского электротехнического института связи (НЭИС).
А.В.Микушин длительное время проработал ведущим инженером в научно исследовательском секторе НЭИС, конструкторско технологическом центре «Сигнал», Научно производственной фирме «Булат». В процессе этой деятельности он внёс вклад в разработку систем радионавигации, радиосвязи и транкинговой связи.
Научные исследования внедрены в аппаратуре радинавигационной системы Loran-C, комплексов мобильной и транкинговой связи «Сигнал-201», авиационной системы передачи данных «Орлан-СТД», отечественном развитии системы SmarTrunkII и радиостанций специального назначения.
Источник
Квадратурная амплитудная модуляция
Квадратурной амплитудной модуляции , или квадратурной амплитудной модуляции (аббревиатура КАМ, английский квадратурная амплитудная модуляция ), представляет собой метод модуляции в электронной коммуникационной технологии , которая сочетает амплитуды модуляции и фазовой модуляции . В специальной литературе он преимущественно считается одним из методов цифровой модуляции , хотя формы аналоговой квадратурной амплитудной модуляции также существуют под названием квадратурная модуляция .
Оглавление
Общее
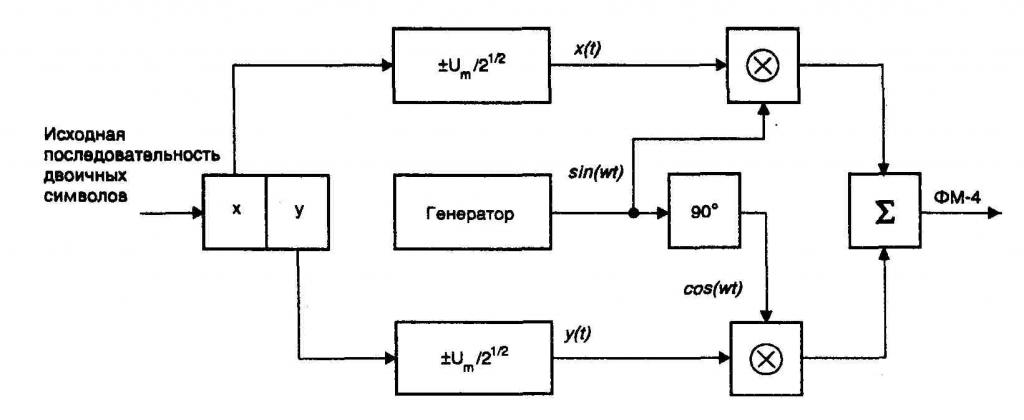
В QAM несущая с угловой частотой ω используется дважды с фазовым сдвигом 90 ° . Затем два независимых сигнала основной полосы частот модулируются с использованием мультипликативного микширования . Затем два модулированных сигнала складываются для получения сигнала передачи. Амплитудную модуляцию двух несущих в квадратуре также можно понимать как амплитудную и фазовую модуляцию одной несущей. Два сигнала основной полосы частот также упоминаются в англоязычной литературе как I для синфазной составляющей и Q для квадратурной составляющей (см. Метод I&Q ), от чего происходит термин IQ модуляция . Не имеет значения, являются ли два сигнала основной полосы непрерывными по времени и значению, например аналоговые цветоразностные сигналы в аналоговом телевидении, или представляют собой непрерывную последовательность символов в контексте цифрового QAM .
Два сигнала основной полосы частот I и Q могут быть выбраны независимо или в зависимости друг от друга. Если два основных сигнала зависят друг от друга согласно определенным правилам, о QAM больше не говорят, хотя структура модулятора не изменилась. Из-за типа зависимости все линейные и нелинейные формы модуляции, такие как амплитудная модуляция (AM), угловая модуляция, такая как частотная модуляция (FM), или модуляция одной боковой полосы, такая как модуляция SSB или VSB , могут быть реализованы с этим. структура модулятора . Программно определяемые радиостанции используют этот факт.
Если два сигнала основной полосы частот I и Q несут информацию, которая не зависит друг от друга, строго говоря, QAM используется только в этом случае, для демодуляции в приемнике несущая должна не только присутствовать на той же частоте, что и модулятор, но и также в той же фазовой позиции. Это также известно как когерентная демодуляция . Если положение фазы было неправильным, части двух независимых сигналов основной полосы частот перекрывались бы и из-за своей независимости мешали бы правильному восстановлению сигнала передачи в приемнике.
Правильное положение фазы должно обеспечиваться дополнительными процедурами, выходящими за рамки процедуры модуляции; процедуры для этого зависят от соответствующего приложения. Например, пакетные сигналы , как в случае цветоразностных сигналов, или дополнительные пилотные тона используются в аналоговых методах QAM . В области передачи цифровых сигналов специальные последовательности синхронизации , которые известны приемнику , периодически передаются в потоке данных. Как часть синхронизации, приемник регулирует положение фазы в демодуляторе до тех пор, пока известные последовательности синхронизации не будут должным образом приняты.
Из-за большей сложности схем на стороне приемника модуляция QAM как аналоговая квадратурная модуляция используется только в определенных областях. Примерами являются стереопроцесс AM и передача двух цветоразностных сигналов в аналоговом цветном телевидении с использованием процесса NTSC или PAL .
Большинство всех приложений QAM находятся в области передачи цифровых сигналов, где потоки цифровых данных изначально делятся между I и Q ветвями. Определенные символы назначаются отдельным битам, и эти последовательности символов преобразуются в непрерывную форму двух сигналов I и Q основной полосы частот с помощью фильтров формирования импульсов .
Дальнейшие разработки QAM в контексте цифровой обработки сигналов приводят к кодированной модуляции, такой как Trellis-Coded Modulation (TCM), где канальное кодирование , например сверточный код , функционально «сливается» с методом модуляции, таким как QAM.
Приложения QAM в контексте цифровой обработки сигналов — это, например, модемы для передачи данных и в области процессов с несколькими несущими, таких как технология DSL , с такими вариантами, как безнесущая амплитудно-фазовая модуляция (CAP). Другими областями применения QAM являются COFDM , где он служит основным методом модуляции и встречается, среди прочего, в стандартах цифрового наземного телевидения согласно DVB-T и DVB-T2 .
Математический фон
Сигнал передачи s (t), как показано на соседнем рисунке, определяется следующим соотношением
s ( т ) знак равно Я. ( т ) ⋅ потому что ( ω т ) — Q ( т ) ⋅ грех ( ω т ) знак равно Я. ( т ) ⋅ потому что ( ω т ) + Q ( т ) ⋅ потому что ( π 2 + ω т ) <\ Displaystyle <\ begin <выровнен>s (t) & = I (t) \ cdot \ cos (\ omega t) -Q (t) \ cdot \ sin (\ omega t) \\ & = I (t) \ cdot \ cos (\ omega t) + Q (t) \ cdot \ cos \ left ( <\ tfrac <\ pi><2>> + \ omega t \ right) \\\ конец <выровнено>>>
формируется из двух сигналов основной полосы частот I (t) и Q (t) в модулятор. Угловая частота означает несущую частоту f . ω знак равно 2 π ж <\ displaystyle \ omega = 2 \ pi f>
s (t) также можно представить с помощью фазы φ (t) и амплитуды A (t) сигнала:
А. ( т ) знак равно Я. ( т ) 2 * Q ( т ) 2 φ ( т ) знак равно а р c т а п ( Q ( т ) Я. ( т ) ) s ( т ) знак равно А. ( т ) ⋅ потому что ( ω т + φ ( т ) ) <\ Displaystyle <\ begin > \ right) \\ s (t) & = A (t) \ cdot \ cos (\ omega t + \ varphi (t)) \\\ конец <выровнен>>>
Демодуляция требует положения фазы, идентичного положению передатчика. Если есть канал передачи без помех , принятый сигнал r (t) равен переданному сигналу s (t), в противном случае к принятому сигналу добавляются компоненты ошибки : е ( т ) <\ Displaystyle е (т)>
р ( т ) знак равно s ( т ) + е ( т ) <\ Displaystyle г (т) = s (т) + е (т) \,>
Сигнал ошибки описывается, помимо прочего, моделью канала. Если ошибок нет, к получению сигнала основной полосы применимо следующее : е ( т ) знак равно 0 <\ Displaystyle е (т) = 0> 
Я. р ( т ) знак равно s ( т ) потому что ( ω т ) знак равно Я. ( т ) потому что ( ω т ) потому что ( ω т ) — Q ( т ) грех ( ω т ) потому что ( ω т ) знак равно 1 2 Я. ( т ) [ 1 + потому что ( 2 ω т ) ] — 1 2 Q ( т ) грех ( 2 ω т ) знак равно 1 2 Я. ( т ) + 1 2 [ Я. ( т ) потому что ( 2 ω т ) — Q ( т ) грех ( 2 ω т ) ] <\ Displaystyle <\ begin
В дополнение к желаемому сигналу основной полосы частот в сигнале создаются смешанные продукты с удвоенной частотой. Эти верхние нежелательные частотные компоненты отфильтровываются последующим фильтром нижних частот (TP), в результате чего исходный сигнал формируется на выходе демодулятора . Я. р ( т ) <\ Displaystyle I_ 

Формирование происходит аналогично: Q р ( т ) <\ Displaystyle Q_
Q р ( т ) знак равно s ( т ) ( — грех ( ω т ) ) знак равно — Я. ( т ) потому что ( ω т ) грех ( ω т ) + Q ( т ) грех ( ω т ) грех ( ω т ) знак равно — 1 2 Я. ( т ) грех ( 2 ω т ) + 1 2 Q ( т ) [ 1 — потому что ( 2 ω т ) ] знак равно 1 2 Q ( т ) — 1 2 [ Я. ( т ) грех ( 2 ω т ) + Q ( т ) потому что ( 2 ω т ) ] <\ Displaystyle <\ begin
и последующая фильтрация нижних частот для формирования . Постоянный коэффициент 1/2, возникающий при и может быть компенсирован усилением. Q ( т ) <\ Displaystyle Q (т)> 

Квантованный QAM
Квантованная QAM расширяет QAM, обычно представленную выше, с помощью методов передачи дискретных значений и дискретных по времени сигнальных последовательностей, также называемых цифровыми сигналами .
Диаграмма созвездия
В цифровом QAM проводится различие между ортогональными сетками и неортогональными сетками. Два сигнала основной полосы частот I и Q в позиции полосы пропускания всегда ортогональны друг другу, что позволяет представить символы в комплексной плоскости в виде диаграммы созвездия . На диаграмме созвездия амплитуда, связанная с символом, соответствует длине вектора, а положение фазы соответствует углу между осью I и этим вектором. Если фазовая позиция приемника не совпадает правильно с фазовой позицией передатчика, диаграмма созвездия вращается в комплексной плоскости, что приводит к соответствующим ошибкам приема. ( Я. Q ) <\ displaystyle <\ begin
Количество доступных символов; они представляют точки или области на этой комплексной плоскости, выражается в форме числа. Например, в спецификации 64-QAM для QAM с объемом 64 символа.
Количество символов на комплексном уровне I / Q представляет собой степень двойки при двоичной передаче, чтобы назначить определенное количество бит отдельным символам (бит на символ / скорость передачи битов). Большое количество символов используется для высокой спектральной эффективности и, если это возможно, с достаточно большим отношением сигнал / шум (SNR). Примеры комбинаций QAM с четным числом битов с назначением двоичных символов:
- 2-битный: 4-QAM — идентичен QPSK или 4-PSK и использует 4 точки в сетке 2 × 2 или на круге, используемом с DVB-S .
- 4 бита: с 16-QAM используются 16 символов, например, приложение со стандартом ITU-R V.29 и с DVB-T
- 6 бит: 64-QAM использует 64 символа, используется с DVB-C и DVB-T
- 8 бит: 256-QAM использует 256 символов, используемых с DVB-C
- 10 бит: 1024-QAM
- 12 бит: 4096-QAM. Это самая большая группировка QAM, рассматриваемая в настоящее время в рамках спецификации DVB-C2, которая едва обнаруживается в лучших условиях — с отношением сигнал / шум 36 дБ. МСЭ-Т стандарт G.hn также использует 4096-QAM в дополнение к обширным кодирования канала
В случае нечетного числа битов на символ требуемая классификация по сетке степени двойки может быть достигнута путем уменьшения пространства созвездия, которое охватывается следующим по величине квадратным числом. Во многих случаях это связано с ухудшением частоты появления ошибок, поэтому эти комбинации QAM используются реже. Примером применения является комбинация кодов контроля четности с низкой плотностью (LDPC) с 8-QAM, где в комбинации с кодированием LDPC достигается лучшая общая эффективность, чем с другими совокупностями QAM.
- 3 бита: с 8-QAM это 8 точек (9 точек в сетке 3 × 3 минус среднее положение дают 8 требуемых позиций — эта модуляция аналогична 8-PSK)
- 5 бит: с 32-QAM это 32 точки (36 точек в сетке 6 × 6 минус одна позиция на угловую точку дают 32 требуемые позиции)
Неортогональная сетка в QAM может дать преимущества с точки зрения символьной синхронизации со стороны приемника. Таким образом, при высокой частоте ошибок некоторые символы могут быть сравнительно легко динамически удалены из диаграммы созвездия. Связанное с этим снижение битовой скорости снижает вероятность ошибок передачи полезного сигнала. Однако недостатком всех неортогональных QAM является более низкая спектральная эффективность по сравнению с компоновкой ортогональных символов . Это связано с тем, что не используется максимально возможная плотность упаковки расположения символов в комплексной плоскости.
Для областей с высоким уровнем помех выбираются созвездия с небольшим количеством символов. Почти во всех случаях для исправления ошибок передачи используется дополнительное канальное кодирование, такое как сверточный код .
16-QAM с допустимыми областями, в которых возможно распознавание уникального символа
Источник