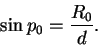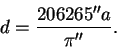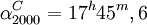Что такое зенитное расстояние солнца

Прямое определение расстояний до сравнительно близких небесных тел основано на явлении параллактического смещения. Суть его заключается в следующем. Близкий предмет при наблюдении его из разных точек проецируется на различные расположенные далеко предметы. Так, держа вертикально карандаш на фоне далекого многоквартирного дома, мы видим его левым и правым глазом на фоне разных окон. Для тел Солнечной системы такое смещение на фоне звезд заметно уже при наблюдении из точек, разнесенных на расстояние, сравнимое с радиусом Земли, а для близких звезд — при наблюдениях из точек, разнесенных на расстояние, сравнимое с радиусом орбиты Земли.

11.1. Горизонтальный экваториальный параллакс

Координаты небесных тел, определенные из разных точек земной поверхности, вообще говоря различны, и называются топоцентрическими координатами. Правда, это заметно лишь для тел Солнечной системы. Для устранения этой неопределенности все координаты тел Солнечной системы приводят к центру Земли и называют геоцентрическими. Угол между направлениями на какое-либо светило из данной точки земной поверхности и из центра Земли называется суточным параллаксом p‘ светила (рис. 22). Очевидно, что суточный параллакс равен нулю для светила, находящегося в зените, и максимален для светила на горизонте. Такой максимальный параллакс называется горизонтальным параллаксом светила p. Горизонтальный параллакс связан с суточным простым соотношением:

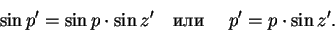(37)

Здесь синусы углов заменены самими углами ввиду их малости.

По сути дела, p — это угол, под которым виден радиус Земли с данного светила. Однако Земля не является идеальным шаром и сплюснута к полюсам. Поэтому на каждой широте радиус Земли свой и горизонтальные параллаксы одного и того же светила разные. Для устранения этих различий принято вычислять горизонтальный параллакс для экваториального радиуса Земли (R₀ = 6378 км) и называть его горизонтальным экваториальным параллаксом p₀.

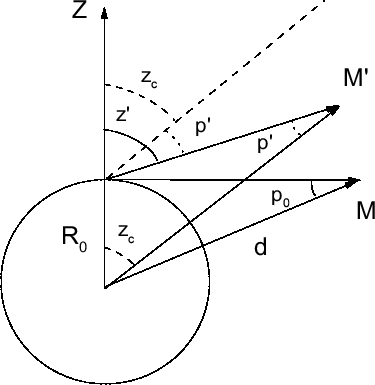Рис. 22. Суточный и горизонтальный параллакс

Суточный параллакс необходимо учитывать при измерении высот и зенитных расстояний тел Солнечной системы и вносить поправку, приводя наблюдение к центру Земли:

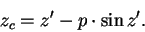(38)

Измерив горизонтальный экваториальный параллакс светила p₀, можно определить расстояние d до него, т.к.

Заменив синус малого угла p₀ значением самого угла, выраженным в радианах, и имея в виду, что 1 радиан равен 206265″, получим искомую формулу:

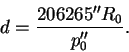(39)

Замена синуса угла самим углом допустима, так как наибольший из известных горизонтальный экваториальный параллакс Луны равен 57′ (у Солнца p₀=8″.79).

В настоящее время расстояния до тел Солнечной системы с гораздо большей точностью измеряются методом радиолокации.

11.2. Годичный параллакс

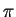
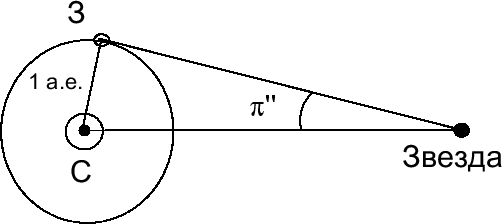Угол, под которым с какой-либо звезды виден радиус земной орбиты a, при условии, что он перпендикулярен направлению на нее, называется годичным параллаксом звезды (рис. 23).

Рис. 23. Годичный параллакс

По аналогии с горизонтальным экваториальным параллаксом, зная годичный параллакс, можно определять расстояния до звезд:

В километрах расстояния до звезд измерять неудобно, поэтому обычно пользуются внесистемной единицей — парсеком пк, определяемой как расстояние, с которого параллакс равен 1″. Само название составлено из первых слогов слов параллакс и секунда. Нетрудно убедиться, что 1 пк = 206 265 а.е. = 3.086 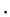10 18 см. Реже используется такая единица измерения расстояний до звезд, как световой год, определяемый как расстояние, проходимое светом за год (1 пк = 3.26 светового года).

Расстояние до звезды в парсеках определяется через величину годичного параллакса особенно просто

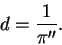(40)

60. (477) Параллакс Солнца p₀=8″.8, а видимый угловой радиус Солнца 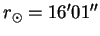. Во сколько раз радиус Солнца больше радиуса Земли?

Решение: Так как параллакс Солнца есть ни что иное, как угловой радиус Земли, видимый с Солнца, следовательно, радиус Солнца во столько же раз больше радиуса Земли, во сколько его угловой диаметр больше параллакса .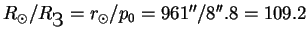

61. (482) В момент кульминации наблюденное зенитное расстояние центра Луны (p₀=57′) было 50 o 00′ 00″. Исправить это наблюдение за влияние рефракции и параллакса.

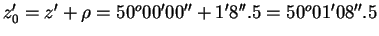
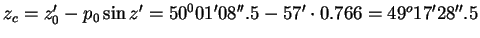
Решение: За счет рефракции наблюденное топоцентрическое зенитное расстояние меньше истинного топоцентрического, т.е. . Истинное топоцентрическое зенитное расстояние больше геоцентрического на величину суточного параллакса .

62.(472) Чему равен горизонтальный параллакс Юпитера, когда он находится от Земли на расстоянии 6 а.е. Горизонтальный параллакс Солнца p₀=8″.8.

63. (474) Наименьшее расстояние Венеры от Земли равно 40 млн. км. В этот момент ее угловой диаметр равен 32″.4. Определить линейный радиус этой планеты.

64. (475) Зная, что для Луны p₀=57’02».7, а ее угловой радиус в это время rЛ=15’32».6, вычислить расстояние до Луны и ее линейный радиус, выраженные в радиусах Земли, а так же площадь поверхности и объем Луны по сравнению с таковыми для Земли.

65. (483) Наблюденное зенитное расстояние верхнего края Солнца составляет 64 o 55′ 33″, а его видимый радиус 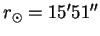. Найти геоцентрическое зенитное расстояние центра Солнца, учтя рефракцию и параллакс.

Читайте также: Крем от солнца колистар

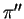
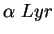
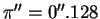
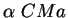
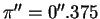
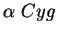
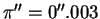
66. Из наблюдений известны годичные параллаксы звезд Вега () , Сириус () , Денеб () . Определить расстояние до этих звезд в пк и в а.е.

Источник

зенитное расстояние Солнца

3.1 зенитное расстояние Солнца: Угол между направлением наблюдения в зенит и на Солнце.

Словарь-справочник терминов нормативно-технической документации . academic.ru . 2015 .

Смотреть что такое «зенитное расстояние Солнца» в других словарях:

Зенитное расстояние — 52. Зенитное расстояние D. Zenitdistans E. Zenith distence F. Distance zénithale Угол между направлениями на зенит данной точки и на другую точку Источник: ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа Смотри также родственные … Словарь-справочник терминов нормативно-технической документации

Зенитное расстояние — Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение… … Википедия

Полярное расстояние — Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение… … Википедия

Маринер-4 — Mariner 4 … Википедия

Астрономия Древней Греции — Астрономия Древней Греции астрономические познания и взгляды тех людей, которые писали на древнегреческом языке, независимо от географического региона: сама Эллада, эллинизированные монархии Востока, Рим или ранняя Византия. Охватывает… … Википедия

Солнечная радиация — Все процессы на поверхности земного шара, каковы бы они ни были, имеют своим источником солнечную энергию. Изучаются ли процессы чисто механические, процессы химические в воздухе, воде, почве, процессы ли физиологические или какие бы то ни было… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Лучистая теплота* — Если какое либо тело нагрето до температуры более высокой, чем окружающие его тела, то опыт показывает, что его температура понижается, а окружающих тел возвышается; следовательно, данное тело теряет теплоту, которую приобретают другие тела. Эта… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Лучистая теплота — Если какое либо тело нагрето до температуры более высокой, чем окружающие его тела, то опыт показывает, что его температура понижается, а окружающих тел возвышается; следовательно, данное тело теряет теплоту, которую приобретают другие тела. Эта… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

РД 52.24.729-2010: Дистанционная спектрометрическая съемка водных объектов в видимом диапазоне волн с мостовых переходов — Терминология РД 52.24.729 2010: Дистанционная спектрометрическая съемка водных объектов в видимом диапазоне волн с мостовых переходов: 3.3 видимые компоненты: Компоненты водной экосистемы, которые изменяют действительную или мнимую части… … Словарь-справочник терминов нормативно-технической документации

Сумерки — У этого термина существуют и другие значения, см. Сумерки (значения) … Википедия

Источник

Зенитное расстояние

Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.

Системы небесных координат отличаются друг от друга выбором основной плоскости и началом отсчёта. В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.

Содержание

Горизонтальная система координат

В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.

Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.

Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.

Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)

Первая экваториальная система координат

В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.

Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.

Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.

Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0 h до +12 h ) к западу и от 0° до −180° (от 0 h до −12 h ) к востоку.

Вторая экваториальная система координат

В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α.

Прямым восхождением (RA,α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере).

RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор в весеннее равноденствие.

Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.

Объект на небесном экваторе имеет склонение 0°
Склонение северного полюса небесной сферы равно +90°
Склонение южного −90°

У склонения всегда указывается знак, даже если склонение положительно.

Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ [1]

Эклиптическая система координат

В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.

Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.

Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.

Галактическая система координат

В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.

Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.

Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.

Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.

Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).

Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:

Изменения координат при вращении небесной сферы

Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.

История и применение

Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.

Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.

Использование различных систем координат

Горизонтальная система координат используется для определения направления на светило с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.

Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.

Вторая экваториальная система координат является общепринятой в астрометрии. В этой системе составляются звёздные карты и описываются положения светил в каталогах.

Эклиптическая система координат используется в теоретической астрономии при определении орбит небесных тел.

Примечания

↑Зигель Ф. Ю. Сокровищница звёздного неба — путеводитель по созвездиям и Луне / Под ред. Г. С. Куликова. — 5-е изд. — М.: Наука, 1986. — С. 57—58. — 296 с. — 200 000 экз.

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое «Зенитное расстояние» в других словарях:

ЗЕНИТНОЕ РАССТОЯНИЕ — угловое расстояние небесного светила или земного предмета от зенита. Обозначается z, отсчитывается вдоль круга высоты от 0 до 180.. С высотой h связано соотношением z = 90. h … Большой Энциклопедический словарь

зенитное расстояние — Угловое расстояние небесного светила или земного предмета от зенита, отсчитываемое вдоль круга высот от 0 до 180°, одна из координат в горизонтальной системе небесных координат … Словарь по географии

зенитное расстояние — Угол между направлениями на зенит данной точки и на другую точку. [ГОСТ 22268 76] Тематики геодезия Обобщающие термины системы координат EN geodetic zenith DE geodätischer Zenit FR zénith géodésique … Справочник технического переводчика

зенитное расстояние — угловое расстояние небесного светила или земного предмета от зенита. Обозначается z, отсчитывается вдоль круга высоты от 0 до 180º. С высотой h связано соотношением z = 90º – h. * * * ЗЕНИТНОЕ РАССТОЯНИЕ ЗЕНИТНОЕ РАССТОЯНИЕ, угловое расстояние… … Энциклопедический словарь

ЗЕНИТНОЕ РАССТОЯНИЕ — угловое расстояние небесного светила или земного предмета от зенита. Обозначается г, отсчитывается вдоль круга высоты от 0 до 180°. С высотой h связано соотношением z = 90° h … Естествознание. Энциклопедический словарь

Зенитное расстояние — угловое расстояние небесного светила от зенита. Обозначается Z и отсчитывается вдоль круга высоты от 0 до 180˚. С высотой h связано соотношением Z = 90˚ h … Астрономический словарь

Зенитное расстояние — одна из координат в горизонтальной системе небесных координат (См. Небесные координаты) … Большая советская энциклопедия

Зенитное расстояние — см. Зенит … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ЗЕНИТНОЕ РАССТОЯНИЕ — см. Небесные координаты … Большой энциклопедический политехнический словарь

Источник