Прямое восхождение
- Прямое восхождение (α, R. A. — от англ. right ascension) — длина дуги небесного экватора от точки весеннего равноденствия до круга склонения светила. Прямое восхождение — одна из координат второй экваториальной системы (есть ещё и первая, в которой используется часовой угол). Вторая координата — склонение.
Прямое восхождение отсчитывается в восточном направлении от точки весеннего равноденствия (то есть в сторону, противоположную суточному вращению небосвода). Для измерения прямого восхождения применяют либо градусную меру (от 0° до 360°), либо часовую меру (от 0h до 24h). При этом 24h = 360°.
Прямое восхождение — астрономический эквивалент земной долготы во второй экваториальной системе. И прямое восхождение, и долгота измеряют угол «восток-запад» вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Начало отсчёта долготы на Земле — нулевой меридиан; начало отсчёта прямого восхождения на небе — точка весеннего равноденствия.
Физический смысл прямого восхождения заключается в том, что если местное истинное звёздное время наблюдателя равно прямому восхождению светила, то оно находится в верхней кульминации — наивысшей, то есть наиболее удобной, возможной для данного места наблюдения точке небесной сферы.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Зени́т-телескóп — телескоп, оптимизированный для наблюдения объектов на относительно малом отклонении от зенита. Он используется при измерении астрономической широты. Такого рода телескопы, как правило, портативны, но это необязательно; примером большого, непортативного зенит-телескопа является Монумент в память о Великом лондонском пожаре (англ. Monument to the Great Fire of London).
Источник
Прямое восхождение — Right ascension
Прямое восхождение (сокращенно RA ; символ α ) — это угловое расстояние до определенной точки, измеренное на восток вдоль небесного экватора от Солнца в мартовское равноденствие до рассматриваемой точки над Землей ( часовой кружок ). В сочетании со склонением эти астрономические координаты определяют положение точки на небесной сфере в экваториальной системе координат .
Старый термин, прямое восхождение ( Latin : Ascensio Recta ) относится к восхождению , или точки на небесном экваторе , который поднимается с любого небесного объекта , как видно из Земли «s экватора , где небесный экватор пересекает горизонт в правом углу . Это контрастирует с наклонным восхождением , точкой на небесном экваторе, которая поднимается вместе с любым небесным объектом, видимым с большинства широт на Земле, где небесный экватор пересекает горизонт под косым углом .
СОДЕРЖАНИЕ
Объяснение
Прямое восхождение — это небесный эквивалент земной долготы . И прямое восхождение, и долгота измеряют угол от основного направления (нулевой точки) на экваторе . Прямое восхождение отсчитывается от Солнца в мартовское равноденствие, то есть от Первой точки Овна , которая является местом на небесной сфере, где Солнце пересекает небесный экватор с юга на север в мартовское равноденствие и в настоящее время находится в созвездии Рыб . Прямое восхождение измеряется непрерывно по полному кругу от этого выравнивания Земли и Солнца в космосе, в это равноденствие, причем измерение увеличивается к востоку.
Для прямого восхождения могли быть выбраны любые единицы измерения угла, но обычно они измеряются в часах ( ч ), минутах ( м ) и секундах ( с ), причем 24 часа соответствуют полному кругу. Астрономы выбрали эту единицу измерения для измерения прямого восхождения, потому что они измеряют местоположение звезды, рассчитывая время ее прохождения через самую высокую точку неба при вращении Земли . Линия, проходящая через самую высокую точку неба, называемую меридианом , является проекцией линии долготы на небесную сферу. Поскольку полный круг содержит 24 часа прямого восхождения или 360 ° ( градусы дуги ), 1 / 24 круга измеряется как 1 ч прямого восхождения, или 15 °; 1 / 1440 круга измеряется как 1 м прямого восхождения или 15 угловых минут (также обозначается как 15 ‘); а также 1 / 86400 круга содержит 1 секунду прямого восхождения или 15 угловых секунд (также записывается как 15 ″). Полный круг, измеренный в единицах прямого восхождения, содержит 24 × 60 × 60 = 86 400 с , или 24 × 60 = 1 440 м , или 24 ч .
Поскольку прямые восхождения измеряются в часах ( вращения Земли ), их можно использовать для определения времени положения объектов на небе. Например, если звезда с RA = 1 ч 30 м 00 с находится на своем меридиане, то звезда с RA = 20 ч 00 м 00 с будет находиться на меридиане / на своем меридиане (в его кажущейся наивысшей точке) 18,5 звездных часов. позже.
Сидерический часовой угол, используемый в астрономической навигации , подобен прямому восхождению, но увеличивается к западу, а не к востоку. Обычно измеряется в градусах (°), это дополнение прямого восхождения по отношению к 24 часам . Важно не путать звездный часовой угол с астрономической концепцией часового угла , которая измеряет угловое расстояние объекта на запад от местного меридиана .
Символы и сокращения
| Ед. изм | Значение | Символ | Шестидесятеричная система | В радианах |
|---|---|---|---|---|
| Час | 1 / 24 круг | час | 15 ° | π / 12 рад |
| Минуты | 1 / 60 час, 1 / 1 440 круг | м | 1 / 4 °, 15 ‘ | π / 720 рад |
| Второй | 1 / 60 минута 1 / 3 600 час, 1 / 86 400 круг | s | 1 / 240 °, 1 / 4 ′, 15 ″ | π / 43 200 рад |
Эффекты прецессии
Ось Земли вращается вокруг небольшого круга (относительно экватора) медленно на запад вокруг полюсов эклиптики, совершая один цикл примерно за 26000 лет. Это движение, известное как прецессия , заставляет координаты неподвижных небесных объектов изменяться непрерывно, хотя и довольно медленно. Следовательно, экваториальные координаты (включая прямое восхождение) по своей сути относятся к году их наблюдения, и астрономы указывают их со ссылкой на конкретный год, известный как эпоха . Координаты из разных эпох должны быть математически повернуты, чтобы соответствовать друг другу или соответствовать стандартной эпохе. Прямое восхождение для «неподвижных звезд» около эклиптики и экватора увеличивается в среднем примерно на 3,05 секунды в год, или на 5,1 минуты за столетие, но для неподвижных звезд, находящихся дальше от эклиптики, скорость изменения может быть любой, от отрицательной бесконечности до положительной бесконечности. Прямое восхождение Полярной звезды быстро увеличивается. Северный полюс эклиптики в Драко и Южный полюс эклиптики в Дорадо всегда на правильном вознесение 18 ч и 6 ч соответственно.
В настоящее время используется стандартная эпоха J2000.0 , которая приходится на 1 января 2000 года в 12:00 TT . Приставка «J» указывает на то, что это юлианская эпоха . До J2000.0 астрономы использовали последовательные бесселевские эпохи B1875.0, B1900.0 и B1950.0.
История
Концепция прямого восхождения была известна, по крайней мере, еще со времен Гиппарха, который измерял звезды в экваториальных координатах во 2 веке до нашей эры. Но Гиппарх и его преемники составили свои звездные каталоги в эклиптических координатах , и использование прямого восхождения ограничивалось особыми случаями.
С изобретением телескопа астрономы получили возможность наблюдать небесные объекты более подробно при условии, что телескоп можно было держать наведенным на объект в течение определенного периода времени. Самый простой способ сделать это — использовать экваториальную монтировку , которая позволяет выровнять телескоп по одному из двух шарниров, параллельных оси Земли. Моторизованный часовой привод часто используется с экваториальной установкой для компенсации вращения Земли . Поскольку экваториальная монтировка получила широкое распространение для наблюдений, для простоты в то же время была принята экваториальная система координат, включающая прямое восхождение. Затем экваториальные монтировки можно было точно направить на объекты с известным прямым восхождением и склонением с помощью установочных кругов . Первый звездный каталог использовать прямое восхождение и склонение было Флемстид «s Historia Coelestis Britannica (1712, 1725).
Источник
Прямое восхождение
Из Википедии — свободной энциклопедии
Прямое восхождение (α; также R. A. — от англ. right ascension ) — координата объекта на небесной сфере, используемая во второй экваториальной системе координат. Прямое восхождение равно длине дуги небесного экватора от точки весеннего равноденствия до круга склонения светила, причём оно отсчитывается против часовой стрелки, если смотреть со стороны северного полюса мира [1] .
Прямое восхождение α вместе со склонением δ образуют вторую экваториальную систему координат — систему небесных координат, общепринятую в астрономии. Прямое восхождение удобно тем, что в отличие от часового угла и азимута не меняется из-за суточного движения.
Прямое восхождение обычно выражается либо в градусной мере (от 0° до 360°), либо в часовой мере (от 0 h до 24 h ), причём 360° и 24 h не включаются. Иногда часовые углы могут отсчитываться к востоку и к западу от точки весеннего равноденствия — по аналогии с долготой. В этом случае они принимают значения от −180° до +180°, или, в часовой мере, от −12 h до +12 h [1] .
| Часовые меры | ||||
|---|---|---|---|---|
| Название | Символ | Значение | Градусная мера | Радианы |
| Час | h | 1 24 окружности | 15° | π 12 рад |
| Минута | m | 1 1440 окружности, | 1 4 °, 15′ | π 720 рад |
| Секунда | s | 1 86400 окружности, 1 3600 часа, | 1 240 °, 1 4 ‘, 15» | π 43 200 рад |
- Точка весеннего равноденствия имеет прямое восхождение 0 h ;
- Точка летнего солнцестояния имеет прямое восхождение 6 h ;
- Точка осеннего равноденствия имеет прямое восхождение 12 h ;
- Точка зимнего солнцестояния имеет прямое восхождение 18 h .
Звёздное время s, часовой угол светила t и его прямое восхождение α связаны:
В момент верхней кульминации часовой угол равняется нулю, следовательно, звёздное время равно прямому восхождению светил в верхней кульминации. Прямое восхождение точки весеннего равноденствия равно нулю, и её часовой угол всегда равен звёздному времени [1] .
Прямое восхождение — астрономический эквивалент земной долготы во второй экваториальной системе. И прямое восхождение, и долгота измеряют угол «восток-запад» вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Начало отсчёта долготы на Земле — нулевой меридиан; начало отсчёта прямого восхождения на небе — точка весеннего равноденствия.
Источник
Формула для прямого восхождения солнца
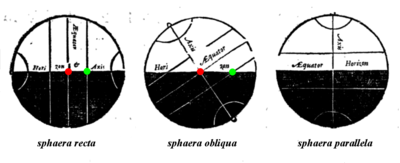
§ 16. Изменение экваториальных координат Солнца
Изменение экваториальных координат Солнца при его движении по эклиптике происходит следующим образом. Когда Солнце находится в точке весеннего равноденствия ^ (см. § 15), его прямое восхождение и склонение равны нулю. Затем с каждым днем прямое восхождение и склонение Солнца увеличиваются, и когда Солнце придет в точку летнего солнцестояния, его прямое восхождение станет равным 90° или б h , а склонение достигает максимального значения + 23° 27‘ . После этого склонение Солнца начинает уменьшаться, а прямое восхождение по-прежнему растет. Когда Солнце придет в точку осеннего равноденствия, его прямое восхождение a = 180° или 12 h , а склонение d = 0°. Далее, прямое восхождение Солнца, продолжая увеличиваться, в точке зимнего солнцестояния становится равным 270° или 18 h , а склонение достигает своего минимального значения — 23° 27′. После этого склонение Солнца начинает расти, и когда Солнце придет в точку весеннего равноденствия, его склонение снова становится равным нулю, а прямое восхождение, достигнув значения 360° или 24 h , обращается в нуль.
Эти изменения экваториальных координат Солнца в течение года происходят неравномерно. Склонение изменяется быстрее всего при движении Солнца вблизи равноденственных точек и медленнее всего — вблизи точек солнцестояний. Прямое восхождение, наоборот, медленнее меняется вблизи равноденственных точек и быстрее — вблизи точек солнцестояний. При этом скорость изменения прямого восхождения Солнца вблизи точки летнего солнцестояния меньше, чем вблизи точки зимнего солнцестояния. Видимое движение Солнца по эклиптике есть следствие действительного движения Земли — обращения ее вокруг Солнца.
Движение Земли вокруг Солнца происходит в том же направлении, что и вращение Земли вокруг оси, и неравномерно (см. § 40). При этом ось вращения Земли всегда наклонена к плоскости орбиты Земли под углом 66° 33‘. Поэтому нам и кажется, что Солнце так же неравномерно перемещается по небесному своду среди звезд, так же с запада на восток, но по окружности (эклиптике), плоскость которой наклонена к плоскости небесного (и земного) экватора под углом 23° 27‘ = 90° — 66°33‘.
Когда Солнце находится в точке весеннего равноденствия ( d = 0), то оно на всех географических широтах земной поверхности восходит в точке востока Е и заходит в точке запада W (см. § 13). Половина его суточного пути находится над горизонтом, половина под горизонтом. Следовательно, на всем земном шаре, кроме полюсов, в этот день продолжительность дня равна продолжительности ночи. Этот день называется днем весеннего равноденствия (около 21 марта) и считается началом весны в северном полушарии Земли. (В южном полушарии этот момент соответствует началу осени.)
Полуденная высота Солнца в день весеннего равноденствия на данной северной широте j согласно формуле (1.7)
Когда Солнце находится в точке летнего солнцестояния ( d = +23° 27′), то оно восходит на данной северной широте j на северо-востоке, а заходит на северо-западе. Большая часть его суточного пути находится над горизонтом. Продолжительность дня в северном полушарии Земли максимальная, ночи — минимальная, в южном — наоборот. Этот день называется днем летнего солнцестояния (около 22 июня) и считается началом лета в северном полушарии Земли (в южном этот момент соответствует началу зимы).
В день летнего солнцестояния полуденная высота Солнца на данной северной широте j достигает максимального значения
h max = 90° — j + 23° 27’
Когда Солнце находится в точке осеннего равноденствия ( d = 0), то оно снова на всей Земле восходит в точке востока и заходит в точке запада, и снова на всех широтах, кроме полюсов, продолжительность дня равна продолжительности ночи. Этот день называется днем осеннего равноденствия (около 23 сентября) и считается началом осени в северном полушарии Земли (началом весны — в южном полушарии).
Высота Солнца в полдень на данной широте j в день осеннего равноденствия снова равна 90° — j .
Наконец, когда Солнце находится в точке зимнего солнцестояния ( d = — 23° 27’), то оно восходит на юго-востоке, а заходит на юго-западе. Большая часть его суточного пути находится под горизонтом. На данной северной географической широте j продолжительность дня минимальна, ночи — максимальна (в южных широтах, наоборот, продолжительность дня максимальна, ночи — минимальна). Этот день называется днем зимнего солнцестояния (около 22 декабря) и считается началом зимы в северном полушарии Земли (началом лета — в южном полушарии).
Высота Солнца в день зимнего солнцестояния на данной северной широте j достигает минимального значения
В остальные дни года высота Солнца в полдень лежит между значениями hmax и hmin .
Источник