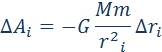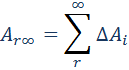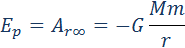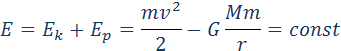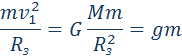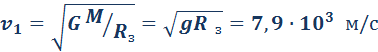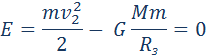Формулы радиуса, орбитальной скорости и периода пл
Формулы для расчета радиуса, скорости орбитального движения и периода планет.
При расчетах используются величины:
— радиус орбиты R (при условном круговом движении) в а.е.
— период T (земной год)
— орбитальная скорость V а.е./год
1. Соотношение радиуса и скорости.
Произведение радиуса и квадрата скорости для всех планет одинаково.
R V2 = const
(получается от преобразований третьего закона Кеплера: R3/ T2 const)
R V2 = R V2 — для разных радиусов обрит разных планет и разных радиусов кривизны одной планеты.
производим вычисления:
для Земли — 1 х 6.28 х 6.28 / 1 = 39.434
где V — 2х 3.14 х R / T 2 х 3.14 х 1 : 1 = 6.28 а.е. /год
для Марса 1.532 х 5.07 х 5.07 = 39.379
скорость для марса : 2 х 3.14 х 1.52 : 1.88 = 5, 07 а.е. / год
радиус орбиты Марса взят средний — он колеблется от 1.405 (перигелий) до 1.693 (афелий)
для Юпитера 5.2 х 2.75 х 2.75 = 39.325
скорость 2 х 3.14 х 5.2 : 11.86 = 2.75 а.е. / год
2. Соотношение радиуса и периода.
Для вычисления периода по радиусу орбиты можно использовать следующую формулу:
Радиус, умноженный на корень квадратный из радиуса, дает период.
(Если единица измерения радиуса — а.е.
то период получается в земных годах.)
получается, что для каждой планеты есть некое число, которое умноженное на себя дает радиус орбиты, а умноженное на себя еще раз — дает период.
Для Марса это число примерно 1.232, для Юпитера 2.28, для Урана 4.38,
для Плутона 6.26 , для Венеры 0.85
Получается числовой ряд планет:
Меркурий 0.62 0.387 0.24
Венера 0.85 0.723 0.615
Земля 1 1 1
Марс 1.232 1.52 1.88
Юпитер 2.28 5.2 11.86
Сатурн 3.09 9.58 29.6
Уран 4.38 19.18 84.048
где: первое это некое базовое число; второе радиус; третье период.
зависимость:1 — число, 2- число возведенное в квадрат, 3- возведенное в куб.
Базовое число планеты — соотношение скоростей Земли и планеты.
А соотношение скоростей Земли и планеты получается из соотношения квадратных корней радиусов этих планет.
Теперь, если взять, например, орбитальную скорость Земли за единицу,
то орбитальная скорость Земли относительно скорости Марса 1.2328.
тогда: радиус обриты Марса есть 1.2328 х 1.2328 = 1.52 а.е.
а период орбиты Марса 1.52 = 1.2328 = 1.8739 в земных годах
что в упрощенной записи :
Vз : V м (Vз :V м ) 2 = R (Vз :V м ) 2 х R = T
или n , далее n в квадрате и n в кубе.
где n Vз :V м — отношение скоростей Земли и Марса.
R V2 = const (получается от преобразований третьего закона Кеплера)
4. Квадрат движения.
Для понимания сути движения планет интересно сделать ещё и такое построение.
Все планеты СС одновременно движутся по своим орбитам. Если взять некий общий отрезок времени,то каждая из планет пройдет за это время по орбите своё раcстояние.
Если на основе этого расстояния, построить квадрат, то площадь этого квадрата для каждой планеты будет пропорциональна орбитальной скорости.
И, если площадь этого квадрата умножить на радиус орбиты, то для всех планет получится одинаковое число, выражающее объём.
И получиться некая константа трехмерного пространства.
Это можно выразить так:
Квадрат расстояния пройденной каждой планетой за общую единицу времени обратно пропорционален радиусам их орбит или произведение радиуса обриты на квадрат расстояния для всех планет за общую единицу времени есть величина одинаковая.
5. Период соединения.
Есть ещё одна формула которая позволяет вычислить через какое время произойдет соединение планет планеты.
Т1 х Т2 / Т2-Т1
6. И, конечно, каждая планета за одну единицу времени проходит угол (сектор), который по отношению к земному, обратно пропорционален периодам.
Формулы могут применяться и для расчета параметров движения спутников.
На рисунке: Таблица соотношения параметров планет Солнечной системы относительно Земли.
комментарии к таблице.
Данные для других планет выражен по отношению к параметрам дв. Земли.
Соотношение скоростей мы понимаем, как соотношение путей пройденных планетой по своей орбите за единицу времени. Соотношение скоростей, возведенное в квадрат дает соотношение радиусов, а возведенное в куб — соотношение периодов планет.
Источник
Формула скорости обращения планеты вокруг солнца
Цель работы: изучение движения тел под действием сил тяготения; проверка третьего закона Кеплера.
На смену геоцентрической системе мира, созданной в начале нашей эры Птолемеем, пришла гелиоцентрическая система, созданная Коперником. Несколько позднее немецкий астроном И. Кеплер на основе астрономических наблюдений установил законы движения планет вокруг Солнца.
Согласно 1-му закону Кеплера любая планета движется вокруг Солнца по замкнутой кривой, которая называется эллипсом (внешне похож на овал). Солнце находится в одном из фокусов этого эллипса. Эллипс имеет два фокуса: это две такие точки внутри кривой, сумма расстояний от которых до произвольной точки эллипса постоянна. Оказывается, что орбиты всех планет Солнечной системы лежат примерно в одной плоскости. Большинство планет движутся по орбитам-эллипсам, которые близки к окружностям. Лишь Марс и Плутон имеют сравнительно вытянутые орбиты.
Второй закон Кеплера устанавливает, что скорость планеты больше тогда, когда она в своем движении находится ближе к Солнцу (в так называемой точке перигелия) и меньше тогда, когда она находится на наибольшем расстоянии от Солнца (в точке афелия). Третий закон Кеплера устанавливает связь между периодом обращения планеты вокруг Солнца и ее средним расстоянием от Солнца, он применяется ко всему коллективу планет Солнечной системы.
Законы Кеплера получили свое объяснение лишь после открытия законов тяготения. Физические объекты участвуют в гравитационном взаимодействии, т.е. они притягиваются друг к другу. Гравитационное взаимодействие обладает всеобщей универсальностью: ему подвержены все материальные объекты и даже физические поля. Закон всемирного тяготения был открыт И. Ньютоном. Он утверждает, что два неподвижных точечных тела взаимодействуют друг с другом с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними, т.е.
 , | (1) |
где γ называют гравитационной постоянной. Этот закон справедлив и для взаимодействия однородных шаров, но в этом случае под r следует понимать расстояние между их центрами.
Рассмотрим движение планеты вокруг Солнца (рис. 1). Планета движется под действием силы F (силы тяготения (1)), которая действует вдоль линии, соединяющей центры тел. Движением Солнца можно пренебречь, так как его масса М гораздо больше массы планеты m. Пусть орбита планеты представляет собой окружность, тогда скорость движения планеты направлена по касательной к этой окружности и перпендикулярно действующей силе. Скорость в этом случае постоянна по величине, поэтому планета движется с центростремительным ускорением. Второй закон Ньютона для этого движения выглядит следующим образом:
Отсюда получаем, что 
. Период обращения планеты вокруг Солнца 
. Выразив из предыдущей формулы v, получаем 
. Возведя правую и левую части этой формулы в квадрат, после преобразований получим:
 . | (2) |
Это и есть третий закон Кеплера, который можно сформулировать следующим образом: отношение куба расстояния от планеты до Солнца к квадрату периода ее обращения вокруг Солнца есть величина постоянная, одинаковая для всех планет Солнечной системы. В случае движения по эллипсу, когда расстояние от планеты до Солнца при движении изменяется, в законе фигурирует некоторое среднее расстояние, т.е. полусумма максимального и минимального расстояний от данной планеты до Солнца. Закон Кеплера справедлив для любой планетной системы, а также для системы спутников какой-либо конкретной планеты, например, для системы спутников Юпитера или Урана. В последнем случае под М в формуле (2) понимается масса соответственно Юпитера или Урана.
Источник
Законы Кеплера
В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.
Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.
Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.
С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (
140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.
 |
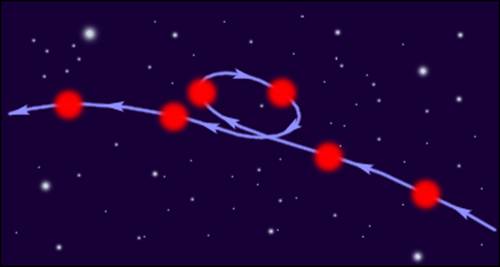| Рисунок 1.24.1. Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд |
Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном Иоганн Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Тихо Браге.
Первый закон Кеплера (1609 г.):
Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удаленная от Солнца – афелием. Расстояние между афелием и перигелием – большая ось эллипса.
 | ||||
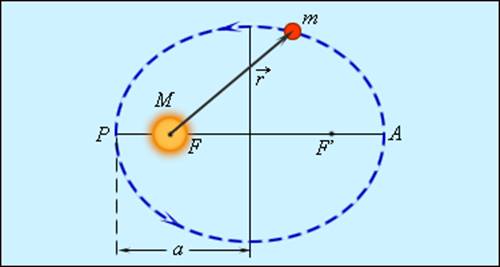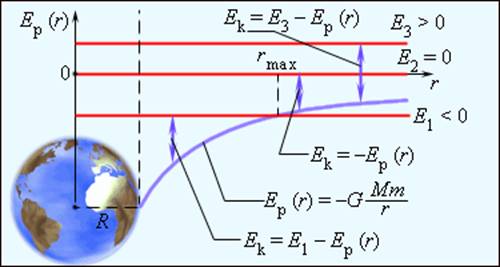
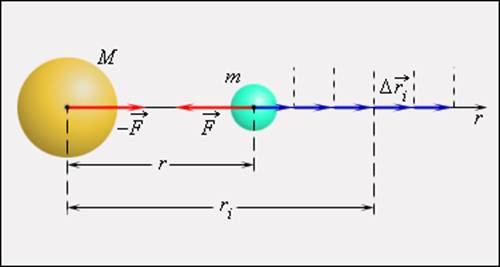
| Рисунок 1.24.2. Эллиптическая орбита планеты массой m –11 Н·м 2 /кг 2 – гравитационная постоянная. Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. В частности, уже говорилось, что сила тяжести, действующая на тела вблизи поверхности Земли, имеет гравитационную природу. Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T 2 R 3 , где Т – период обращения, R – радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца:
Свойство консервативности гравитационных сил позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки. Потенциальная энергия тела массы m, находящегося на расстоянии r от неподвижного тела массы M, равна работе гравитационных сил при перемещении массы m из данной точки в бесконечность. Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях (рис. 1.24.5).
Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. Работа
Полная работа при перемещении тела массой m из начального положения в бесконечность находится суммированием работ ΔAi на малых перемещениях:
В пределе при Δri → 0 эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение
Знак «минус» указывает на то, что гравитационные силы являются силами притяжения. Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость υ, его полная механическая энергия равна
В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной. Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1.24.6). При E = E1 rmax. В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы).
При E = E2 = 0 тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории. При E = E3 > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии. Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля. Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли. Эту скорость необходимо набрать, чтобы преодолеть притяжение Земли и вывести тело (например, спутник) на орбиту Земли.
Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.
Рис. 1.24.7 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9·10 3 м/с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих υ1, но меньших υ2 = 11,2·10 3 м/с, орбита корабля будет эллиптической. При начальной скорости υ2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе. Источник ➤ Adblockdetector |
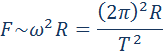
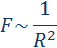
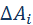гравитационной силы 
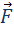на малом перемещении 
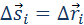есть:
