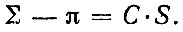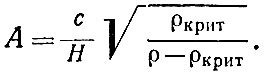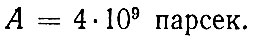Геометрические тела во вселенной
§ 2. Геометрические свойства пространства Вселенной
Обратимся теперь к космологии и будем рассматривать области пространства, сравнимые с Rкрит и большие, чем Rкрит (определенный в § 12 гл. 1), при исследовании которых надо использовать релятивистскую теорию.
Мы будем рассматривать большие области пространства, в которых распределение материи можно считать однородным (см. гл. 1) и все свойства не зависят от направления. Как уже было сказано во введении к книге, космологическая модель при таких предположениях была построена А. А. Фридманом на основе теории Эйнштейна.
Нас сейчас будет интересовать главным образом искривление, геометрия трехмерного пространства, но всегда надо помнмъ, что в общей теории относительности искривлено, не только трехмерное пространство, но и четырехмерное пространство-время.
Еще раз напомним, что все эти усложнения по сравнению с классическими представлениями механики Ньютона необходимы. В механике Ньютона было абсолютное пространство и в нем двигались тела. Специальная теория относительности показала, что абсолютного пространства нет, нет абсолютного движения и для определения движения надо вводить систему отсчета. Только после указания системы отсчета имеет смысл говорить, как по отношению к ней движутся тела. Общая теория относительности показала, что пространство-время искривлено в зависимости от тяготения вещества (точнее, искривление и есть проявление тяготения). Если тяготеющее вещество движется, то искривление меняется со временем. Значит, любая система отсчета будет изменяться, деформироваться. Таким образом, нет жесткого каркаса-сетки неизменных пространственных координат, все они в переменных гравитационных полях обязаны деформироваться * .
* ( Разумеется, в слабых полях все деформации в сетке координат, связанные с изменением кривизны пространства — времени, могут быть сделаны пренебрежимо малыми. Иное дело в космологии, когда мы охватываем большие массы вещества; здесь изменения искривления пространства — времени велики и жесткая сетка координат неприменима. Вот почему мы говорили в §4, что теряет однозначный смысл утверждение о скорости удаления очень далеких галактик. Ведь к ним не протянуть мысленно, даже в принципе, жестких масштабных стержней, по отношению к которым определяется скорость. Специальная теория относительности установила, что нет абсолютного пространства, нет абсолютной скорости. Но согласно этой теории, после того как выбрано состояние движения наблюдателя, с ним можно связать мысленно жесткую сетку координат и по отношению к ней измерять скорость тел на любом расстоянии от наблюдателя. Общая теория относительности утверждает, что в полях тяготения и после выбора наблюдателя абсолютно жесткой протяженной сетки координат с ним не свяжешь, поэтому и нет однозначного определения скорости далеких галактик (для таких расстояний неизбежные деформации сетки особенно велики). Но отсутствие однозначного определения скорости удаления галактик не мешает теории Эйнштейна точно и однозначно вычислять красное смещение спектральных линий далеких объектов, видимую яркость объектов и другие наблюдаемые величины.)
После этих необходимых кратких разъяснений вернемся к космологии. В однородной изотропной космологической модели Фридмана выбор системы отсчета естествен. Выберем систему отсчета как координатный каркас, расширяющийся вместе с системой галактик (точнее, скоплений галактик). Галактики по отношению к этому каркасу покоятся * . Такая система отсчета получила название сопутствующей. Мы будем ею пользоваться и изучать геометрические свойства «сопутствующего», как говорят, пространства этой системы отсчета.
* ( Галактики, помимо общей скорости расширения, имеют еще сравнительно небольшие случайные скорости. Эти скорости составляют обычно сотни (иногда тысячи) км /сек. Мы не рассматриваем здесь случайные скорости галактик, усредняем их движение.)
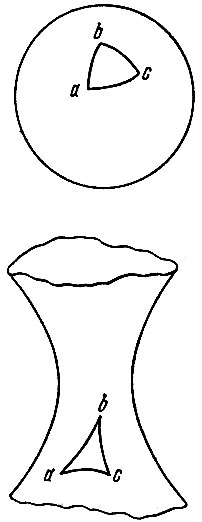
Что такое искривление пространства? Это изменение его геометрических свойств. Мы наглядно можем пред-ставить себе искривленную двумерную поверхность (например, поверхность шара, или поверхность гиперболоида; рис. 18). На таких поверхностях геометрия отличается от геометрии на плоскости. Однако эта аналогия вряд ли поможет нам представить наглядно искривленное трехмерное пространство. Мы живем в трехмерном пространстве, выпрыгнуть из него не можем (так как вне пространства ничего нет), поэтому нельзя спрашивать: «в чем изгибается наше реальное пространство? * . Суть кривизны пространства заключается в изменении его геометрических свойств по сравнению со свойствами плоского пространства, где справедлива геометрия Евклида.
* ( Хотя, конечно, в математике рассматривается «вложение» искривленного трехмерного пространства в воображаемые пространства большего числа измерений.)
В искривленном пространстве аналогом плоскостей являются геодезические поверхности, аналогом прямых- геодезические линии. Как уже говорилось, треугольник из геодезических линий имеет в искривленном пространстве сумму углов, отличную от я (или, что то же, от 180°) и зависящую от площади, длина окружности не равна 2πr и т. д. Кривизна двумерной поверхности в данной точке характеризуется одним числом. Это число определяется следующим образом. Измеряется сумма углов деляется следующим ооразом. измеряв маленького треугольника, начерченного вокруг данной точки. На кривой поверхности она либо больше, либо меньше, чем π. Можно доказать, что разность суммы углов ∑ и π пропорциональна площади треугольника S:
Коэффициент пропорциональности С называют кривизной. Величина С может быть и положительна и отрицательна. Корень квадратный из величины 1 /С называют радиусом кривизны. Если С отрицательно, то радиус кривизны мнимый. Например, на поверхности шара (во всех точках кривизна, естественно, одинакова) — положительна, и равна квадрату радиуса шара; радиус кривизны есть радиус шара. Примером поверхности отрицательной кривизны является поверхность однополостного гиперболоида на рис. 18.
Рис. 18. Двумерные искривленные поверхности. Вверху: сфера — поверхность с положительной кривизной. Сумма углов треугольника на сфере больше π. Внизу: однополостный гиперболоид — поверхность с отрицательной кривизной. Сумма углов треугольника на гиперболоиде меньше π
Кривизна трехмерного пространства — понятие более сложное. Но нас интересует сейчас простой случай однородной изотропной Вселенной. Здесь кривизна пространства характеризуется также одним числом — кривизной, которое определяется как и для поверхности. Уравнения общей теории относительности показывают, что если плотность материи во Вселенной меньше критического значения (см. гл. 1) ρкрит = 10 -29 г /см 3 , то кривизна пространства отрицательна, если же больше этого значения, то кривизна положительна.
Величина кривизны и ее знак в однородной Вселенной одинаковы во всех точках пространства в один и тот же момент времени. Величина радиуса кривизны зависит от постоянной Хаббла H и плотности вещества и выражается формулой
Здесь с — скорость света. Так, для плотности ρ, в два раза превышающей критическое значение, получаем радиус кривизны
Если плотность вещества меньше критической, то радиус кривизны мнимый, а сама кривизна (являющаяся квадратом радиуса кривизны) — отрицательна. В этом случае характеристикой искривленности является абсолютная величина мнимого радиуса.
Плотность вещества и постоянная Хаббла меняются с течением времени, меняется и радиус кривизны, но знак кривизны неизменен в течение всей эволюции. Радиус кривизны меняется со временем точно так же, как и расстояние между любой парой галактик. Поэтому график рис. 9 является одновременно и графиком для изменения с течением времени величины А. Для случая ρ ρкрит величина А растет, достигает максимума и снова уменьшается до нуля.
Источник
Геометрические тела во вселенной

Свойства пространства и времени не абсолютны, не заданы раз навсегда, а зависят от распределения и движения тяготеющих масс. Это — центральная идея релятивистской физики, общей теории относительности Эйнштейна. Поэтому пространство, однородно заполненное материей, и само должно быть однородным, всюду одинаковым по своим геометрическим свойствам. Распространяя свойство однородности, установленное наблюдениями близкого к нам объема Вселенной, на всю Вселенную, мы делаем, конечно, предположение (по-видимому, разумное), что наблюдаемый участок ничем специально не выделен во Вселенной и вся она всюду одинакова. Физическое пространство однородно, но оно может быть искривлено тяготением материи, гравитацией. Трехмерное пространство способно быть кривым, неевклидовым, подобно тому, как искривлены двумерные поверхности, скажем, поверхность сферы или псевдосферы. Хотя наглядное представление искривленных трехмерных пространств затруднительно, переход к ним от двумерных кривых поверхностей можно вообразить по примеру перехода от плоскости (евклидовой двумерной поверхности) к привычному трехмерному евклидову пространству, перенося на трехмерные образы геометрические свойства двумерных прототипов. Так, можно ожидать, что трехмерный аналог сферы должен иметь конечный объем, подобно тому, как сфера имеет конечную площадь. Это пример конечного трехмерного пространства. Напротив, трехмерный аналог псевдосферы должен иметь бесконечный объем, как бесконечна полная площадь псевдосферы. Это — пример бесконечного пространства. Промежуточная возможность — неискривленное, евклидово трехмерное пространство; у него тоже бесконечный объем (как бесконечна площадь неограниченной плоскости). Каково же реальное пространство однородной Вселенной? Ответ могли бы дать непосредственные геометрические измерения с помощью лучей света, посылаемых галактиками. Но на тех расстояниях, на которых они видны, отклонения от свойств привычного евклидова пространства еще неуловимы.
Пространство могло бы проявить свою кривизну только на гораздо больших расстояниях. Но там реальные измерения невозможны: мало ярких источников света. Возможно, однако, иное решение вопроса, исходящее из общих представлений релятивистской физики о связи между геометрией пространства и тяготеющими массами. Если взаимное разбегание космических тел — скоплений, сверхскоплений — будет продолжаться неограниченно и расстояния между телами будут возрастать, стремясь с течением времени к бесконечности, то, по теории Фридмана, неограниченным, бесконечным должен быть и объем пространства, в котором они движутся. По геометрическим свойствам такое пространство должно быть подобно псевдосфере. Напротив, ограниченность расширения во времени и возможность перехода в будущем к сжатию означает и пространственную ограниченность, конечность объема Вселенной, которая в этом случае подобна сфере по своей геометрии. Когда говорят об однородности распределения вещества, подразумевают, что видят сразу всю картину разбегающихся космических систем как бы одновременно. В самом деле, так как плотность вещества во Вселенной убывает в ходе космологического расширения, то считать среднюю плотность мира всюду одинаковой можно только при том условии, что каждый участок Вселенной рассматривается на одном и том же этапе расширения — в этом и состоит в данном случае смысл одновременности. Иначе один участок выглядел бы более плотным (т. е. «молодым»), а другой — менее плотным («старым»), если бы мы видели первый на более раннем, а второй на более позднем этапе расширения. Можно сказать, что однородность плотности существует лишь на «мгновенной» фотографии Вселенной, снятой в таких воображаемых «лучах», которые распространяются мгновенно, с бесконечной скоростью, и именно на таком снимке мир в целом и предстает перед нами однородным. Конечно, мгновенно распространяющихся волн или лучей в природе нет; любые сигналы распространяются с конечными скоростями и самая большая из них — скорость света. Как выглядел бы мир, «снятый» в реальных световых лучах? Астрономические наблюдения — оптические и радио, в инфракрасных, ультрафиолетовых, рентгеновских и гамма-лучах — производятся с помощью электромагнитных волн различной частоты и длины волны. Они показывают картину неба с запаздыванием, так как волнам требуется определенное время, чтобы пройти разделяющее нас и наблюдаемый объект расстояние. Солнце мы видим с задержкой на 8 минут. Свет от звезд Галактики идет десятки и сотни лет, а от далеких галактик и скоплений,— миллионы и сотни миллионов лет.

Чем дальше объект, тем в более раннюю эпоху мы его видим. Дальше всех находятся квазары, и мы видим их такими, какими они были миллиарды лет назад. Наблюдая распределение и движение галактик, скоплений, сверхскоплений, мы узнаем эти их свойства такими, какими они были в очень отдаленном, по нашим обычным понятиям, прошлом. Но по масштабам Вселенной разница в сотни миллионов лет не очень велика: ее расширение происходит в таком темпе, что плотность вещества Вселенной на современной стадии ее расширения заметно меняется лишь за миллиарды лет. Потому-то плотность в близкой к нам области Вселенной, где видны галактики, и представляется нам одинаковой, однородной. Если бы, однако, можно было заглянуть на более далекие расстояния, т. е. в более далекое прошлое, то мы, очевидно, обнаружили бы, что там (т. е. тогда) плотность больше, чем вблизи (т. е. сейчас). Снимок, сделанный в реальных лучах, показал бы, таким образом, Вселенную неоднородной по плотности: чем дальше от нас, тем плотнее. На таком снимке и само пространство, в соответствии с общими принципами эйнштейновской теории, должно быть неоднородным по своим геометрическим свойствам. Более того, на снимке в реальных лучах пространство всегда конечно по объему, независимо от того, какова судьба космологического расширения. Дело в том, что свет, приходящий к нам от далеких источников, испытывает за время своего распространения красное смещение: длины волн в электромагнитных колебаниях возрастают, а частоты убывают. Это, как мы говорили, следствие эффекта Доплера, обязанного космологическому расширению, относительному движению галактик. По закону Хаббла, чем дальше от нас источник, тем больше скорость его удаления от нас и, следовательно, больше красное смещение линий в его спектре. При этом существует такое большое, но вполне определенное, конечное расстояние, для которого длина волны приходящего света оказывается бесконечной, а частота принимаемого света обращается в нуль, и из-за этого источник становится для нас невидимым.
Таким образом, можно говорить о существовании во Вселенной горизонта, в пределах которого только и возможны наблюдения. Объем пространства, доступный наблюдениям, оказывается по этой причине конечным: конечна и содержащаяся в нем масса вещества. Расстояние до горизонта, которое в современную эпоху равно примерно 15—18 миллиардам световых лет, есть путь, который свет успевает пройти за 15—18 миллиардов лет от начала космологического расширения до настоящего момента. Вывод о существовании горизонта никак не зависит от того, есть ли в действительности астрономические объекты, которые так ярки, что могут посылать нам свет со сколь угодно больших расстояний. Он имеет характер принципиального ограничения, вытекающего фактически из того обстоятельства, что все волны и лучи проходят за конечное время конечное расстояние. Горизонт как предел видимости — это, очевидно, и предел любого обмена сигналами, а значит, и предел причинной связи. Два события могут быть между собой причинно связаны,— так, например, чтобы одно было следствием другого,— только если оба они происходят в пределах горизонта. Горизонт расширяется вместе с расширением Вселенной; его радиус возрастает как путь, проходимый светом за время от начала расширения, и в каждую последующую эпоху в пределах горизонта оказывается больше вещества, чем в предыдущую. Те области Вселенной, которые сейчас находятся в пределах современного горизонта и заняты видимыми галактиками, были когда-то раньше разделены горизонтом. Горизонт, как непроницаемая стена, изолировал их, они ничего «не знали» тогда друг о друге. Но, войдя сейчас в контакт, они «обнаруживают», что имеют одну и ту же плотность. Почему? Каким образом распределение и движение вещества оказались скоррелированными в этих различных и далеко отстоящих друг от друга участках мира? Ответ на этот вопрос пока не найден. Остается лишь полагать, что мир «с самого начала» был однородным, а космологическое расширение всегда происходило в одинаковом темпе во всех его областях. Но что значит «с самого начала», и что было «до этого» — вопросы, ответить на которые, может быть, еще труднее, чем на вопрос о причинной связности Вселенной.
Фридрих Вильгельм Бессель. К 220 — летию со дня рождения Фридрих Вильгельм Бессель родился 22 июля 1784 г. в г. Миндене в Вестфалии (ныне в ФРГ) в семье мелкого судебного чиновника и с 15 лет должен был встать на самостоятельный трудовой путь. Правда, это вполне отвечало тогда и его желаниям: с ранних лет ему было свойственно стремление к практической деятельности и лишь к тем знаниям, которые .
Задача 1 За первый час было расчищено от снега всей дороги, а за второй час всей дороги. Какая часть дороги была расчищена от снега за эти два часа? На какую часть дороги было расчищено меньше в первый час, чем во второй? Для того, чтобы узнать, какая часть дороги была расчищена за два часа, надо сложить и . Получим: Значит, за эти два часа было расчищено всей .
Европейцы чаще именовали Иран Персией, переняв название от древних греков. Но в 1953 году правительство страны официально утвердило за ней местное древнее название Иран. Иран — крупное многонациональное государство с населением около 26 млн. человек (1996 г.), по площади — 1648 тыс. кв. км. — уступает в зарубежной Азии лишь Китаю, Индии, Индонезии и Саудовской Аравии. Природа и ландшафт Ирана .
Задачи в стихах Задачи Эти задания рекомендуются для подготовки детей к школе. Если ребенок затрудняется решить задачу в устной форме, предложите ему ее нарисовать или решить с помощью счетных палочек, пуговиц. У мышки два ушка. Сколько ушей у двух мышей? На крыльце сидит щенок, Греет свой пушистый бок. Прибежал еще один И уселся рядом с ним. (Сколько .
Источник