Геометрия пространства геометрия вселенной

Геометрия пространства

Рубрика «Читатели пишут»

«Никакое рассмотрение частных вопросов о Вселенной – результатов исследований, установление фактов, гипотез, предположений и фантазий — не дадут в итоге описания Вселенной, близкое к истинному. Потому, что исходная информация значительно ограничена.

Первым посылом должно быть утверждение: Вселенная есть Система.

Система должна иметь системные признаки, т. е. неизменные, постоянные и везде присутствующие определения-характеристики. В физике такими основами следует считать пространство, время, энергия, информация (Вместе с тем, все четыре указанные основы должны быть, в свою очередь, связаны между собой системно!). В философии основами Вселенной принято считать некие архетипы, имеющие начало и пронизывающие всю Вселенную.

Всё, что указано здесь как основы Вселенной, не определено не в физике, не в философии. С указанных основ и с их определений и следует начинать рассмотрение возникновения и состояния Вселенной.

Из поставленных вопросов, как мне представляется, проще всего определиться с геометрией пространства.

1. Геометрия пространства не эвклидова, поскольку во Вселенной нет прямых линий, кроме линий, лично проведённых фантазирующим умом.

2. Земля движется относительно центра Галактики по спирали: год – виток спирали. Орбита Земли вокруг Солнца не замкнута. Земля движется по своей орбите без какой-либо дополнительной энергии, можно сказать, что Земля движется естественным порядком.

3. Луна по своей орбите движется вокруг Земли. Но её орбита не замкнута – Луна движется без каких-либо дополнительных приложений энергии по спирали. Так же можно рассматривать и всякое иное движение во Вселенной.

4. Всякая спираль движущегося во вселенной космического объекта выписывает незамкнутый тор. Объём Земли так же исполняет тор своей орбиты.

5. Всякий тор движения объектов космоса представляет собой некоторую трубу, всегда в большей или меньшей мере изогнутую, с незначительным расширением с течением времени.

6. Итог. Геометрия пространства во Вселенной соответствует геометрии Лобачевского. Я назвал описанную геометрию Вселенной Законом числа ПИ (2010 г.), поскольку именно иррациональное число ПИ указывает на отсутствие во Вселенной замкнутого круга при движении. Конечно, к этому же итогу могут подвести нас и иные исследования.»

Источник

Геометрия Вселенной

Прежде чем рассказывать о чем-то из области современной науки, надо условиться внимательно обдумывать все аргументы и по возможности не прибегать к слову «очевидно». Это — очень опасное слово. В древности казалось, очевидно, что Земля не может быть шаром. «Иначе,— говорили ученые — скептики, — люди с другой стороны должны были бы ходить вниз головой, и они бы упали — это же очевидно!» В наше время в школе без особого труда объясняют даже маленьким ученикам и ученицам, что Земля шарообразна, а не падают люди с нее потому, что понятия «верх» и «низ» на Земле не имеют абсолютного смысла и являются не вполне точным выражением направлений к центру планеты и от него. И нам теперь очевидно, что Солнце не может каждый вечер погружаться в мировой океан, который будто бы окружает Землю-блин, что Земля не может стоять на трех китах и т. д.

Не только физика выясняла, что природа устроена совсем не так, как «видят очи». К этому выводу приводит нас вся деятельность человека. Чтобы узнать свойства окружающего нас мира, надо тщательно переработать информацию, которую получают органы чувств. И самый главный урок, который дала нам природа, состоит в том, что только правильно поставленный опыт может выяснить физическую сущность явлений и что никакие теоретические построения, какими бы они ни казались очевидными, но могут без опыта ответить на вопросы, касающиеся устройства физического мира.

Если все, что здесь сказано, не вызывает возражений, мы можем перейти к нашей основной теме.

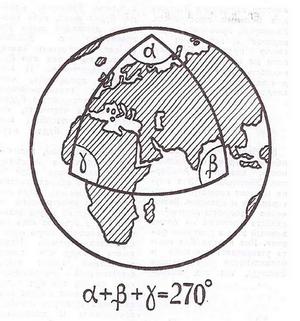
В школе учат геометрию Эвклида. Определяют точку, прямую, плоскость аксиомами и не замечают, что правильность описания этими аксиомами результатов измерений в реальном мире ниоткуда не следует. Позже эти аксиомы переносятся в механику, и опять вопрос о проверке их на опыте не выясняется. Но всякая теория должна быть проверена на опыте, и в особенности — выводы геометрии Эвклида. Действительно, откуда мы знаем, что сумма углов треугольника равна 180? Если измерить с большой точностью углы треугольника, построенного на футбольном поле, то это окажется так. Но если бы мы построили треугольник, поместив одну вершину на Северном полюсе, а две других — на экваторе (на долготе Гринвича и на 90 восточной долготы), то в таком треугольнике каждый угол будет равен 90° и, следовательно, их сумме — 270°.

Могут возразить; в школьной теореме говорится о плоском треугольнике, а не о треугольнике, нарисованном на поверхности шара. Но, строя треугольник на поверхности Земли (для наглядности глобуса), мы тоже проводим «прямые линии» — кратчайшие между двумя точками линии на сферической поверхности. Это дуги большого круга.

Свойства поверхности шара, одно из которых мы сейчас рассмотрели, и образуют геометрию сферы. Мы видим, что геометрия сферы отличается от геометрии плоскости, и нетрудно понять, что каждая поверхность имеет свою геометрию. На примере суммы углов треугольника мы видим, кроме того, что можно изучать геометрию поверхности, не уходя с нее самой, а лишь измеряя характеристики фигур, нарисованных на ней. По крайней мере, в принципе можно получить все сведения о поверхности земного шара, производя на ней геодезическую съемку.

В МИРЕ ТРЕХ ИЗМЕРЕНИЙ

Мы сравнительно легко можем убедиться в разных свойствах сферы и плоскости. В трехмерном мире картина значительно сложнее. Зададимся снова вопросом: чему равна сумма углов треугольника, вершины которого лежат, например, на Солнце, Сириусе и на ближайшей к нам звезде — альфе Центавра. По геометрии Эвклида сумма углов треугольника равна 180. Но как проверить такое утверждение? Ссылка на то, что опыты на Земле подтверждают теорему, ничего не доказывает. Справедливое на малых расстояниях может оказаться неверным для больших.

На примере сферического треугольника мы видели, что отклонение от свойств плоских треугольников тем больше, чем больше треугольник. С другой стороны, у нас нет никаких способов измерить сумму углов такого большого треугольника. Более того, даже эти расстояния могут оказаться недостаточными, чтобы обнаружить отклонения от законов геометрии Эвклида. Отсюда следуют два вывода. Во-первых, у нас нет доказательств справедливости геометрии Эвклида для больших пространств. Во-вторых, проверить справедливость геометрии не так-то просто. Поэтому, если не ссылаться на очевидность, надо искать пути для экспериментального исследования вопроса.

ПРОСТРАНСТВО И ВРЕМЯ

Проблема была решена общей теорией относительности, созданной Альбертом Эйнштейном. Эта наука изучает геометрию пространства и времени. Включение в вопросы геометрии свойств времени — очень важный этап в развитии науки. Как нельзя без опыта утверждать что-либо о правильности геометрии Эвклида, так же, оказывается, у нас нет никаких оснований считать, что геометрические свойства нашего мира представляются одинаковыми движущемуся наблюдателю и наблюдателю, находящемуся в покое.

Специальная теория относительности установила, что движущиеся тела сокращаются в направлении движения. Поэтому измерение расстояния между двумя точками в пространстве с помощью натянутой веревки или же по времени, которое надо затратить для переезда из одной точки в другую с известной скоростью, дает разные результаты. Различие, правда, будет мало, если скорость движения мала по сравнению с 300 000 км/сек.— скоростью света, но, тем не менее, оно будет существовать. И мы должны предвидеть, что проверка геометрических свойств пространства будет зависеть, в частности, от того, каким способом мы эти свойства будем изучать.

Таким образом, геометрия и движение оказываются связанными друг с другом. Это обстоятельство и подразумевают, когда говорят, что пространство и время друг от друга зависят. Часто говорят еще о четырехмерном мире «пространство — время». Надо иметь в виду, что такое выражение имеет лишь формальный математический смысл, так как ясно, что ни в каких опытах или явлениях пространственные координаты и показания часов не могут быть перепутаны.

Чтобы изучать геометрию мира, надо, прежде всего, уметь провести прямую линию. Это можно сделать разными способами. Можно просто натянуть нитку между двумя точками. Можно прочертить прямую линию как траекторию тела, движущегося по инерции. Можно, наконец, прямой линией назвать путь луча света. В обычных, земных условиях мы должны следить, чтобы она не провисала, чтобы вес ее был мал и земное притяжение практически не изменяло ее форму. Наблюдая за движением тела, мы должны быть уверены, что на него не действуют никакие силы и оно действительно движется по инерции. Наконец, когда мы будем производить построение с помощью луча света, необходимо проверить оптическую однородность среды, чтобы быть уверенным, что свет не преломляется. Как бы мы ни начинали построение, мы сразу же уходим от чистой геометрии и должны производить настоящий физический опыт.

В таком опыте прежде всего обнаружится, что его результаты не абсолютно точны, а им сопутствует какая-то, пусть даже и очень небольшая, ошибка. В отличие от геометрических аксиом, которые точны по определению, геометрию реального мира мы определим лишь приближенно. Ясно, что, проводя опыт не в земных, а в космических условиях, трудно придерживаться всех перечисленных правил. Поэтому опыты должны быть поставлены так, чтобы они даже при небольшой точности позволили качественно изучить геометрию.

Основным выводом общей теории относительности было утверждение, что геометрия нашего мира не эвклидова. Отклонение от законов геометрии Эвклида сказывается прежде всего в том, что тело при отсутствии внешних сил движется не по прямой. Такое отклонение траектории от прямой воспринимается наблюдателем как движение тела под действием какой-то внешней силы, которую привыкли называть силой тяготения. Это значит, что тяготение резко отличается от других сил, которые действуют в природе, электромагнитных и ядерных. Наблюдатель описывает движение тел понятиями геометрии Эвклида и механики Ньютона и любые отклонения от теорем этих наук объясняет наличием новых сил. Сведение сил тяготения к геометрическим свойствам Вселенной позволило решить одну из труднейших проблем естествознания. В связи с этим общую теорию относительности часто называют теорией тяготения.

Автор: А. Я. Смродинский.

P. S. О чем еще говорят британские ученые: о том, что геометрия Вселенной помимо всего прочего заключает в себе все знания человечества, будь то русский язык онлайн, особенности дорийского искусства или строения хромосом простых организмов.

Источник

Научно-эзотерические основы мироздания. Жить, чтобы знать. Книга 2
Виталий Тихоплав

Во второй части книги «Научно-эзотерические основы мироздания» авторы систематизируют открытия и достижения мировой науки в области атомной и субатомной физики. Выводы, к которым они приходят, удивительным образом совпадают с основными идеями восточной философии о духовной основе жизни, иллюзорности мира и законе кармы. Исследование супругов Тихоплав наглядно демонстрирует, как близко подошла наука к признанию божественной основы мироздания. Вполне вероятно, что решающий шаг в этом сближении не только перевернет наши представления об устройстве вселенной и эволюции человечества, но и укажет нам наиболее перспективный путь дальнейшего развития.

Приведённый ознакомительный фрагмент книги Научно-эзотерические основы мироздания. Жить, чтобы знать. Книга 2 предоставлен нашим книжным партнёром — компанией ЛитРес.

Куда бежите вы, пьяные люди? Вы выпили до дна из чаши неразбавленного вина невежества и не можете переварить его, вас уже тошнит от него. Отрезвитесь, откройте очи вашего сердца, если не все вы, то, по крайней мере, те, кто может. Ибо потоп невежества наводнил землю, развращает души, заточенные в теле, и мешает им войти в спасительную гавань.

Гермес Трисмегист, IV век до нашей эры, Египет

Лекция № 13. Геометрия пространства

Итак, эфир по-прежнему неуловим, свет не подчиняется правилу сложения скоростей, принятому в классической физике. Какие еще «неприятности» могут ждать ученых на новом пути, который начала прокладывать в науке релятивистская физика?

И эти «неприятности» возникли в самом, казалось бы, неожиданном месте, в основе основ — в геометрии пространства Евклида! Трудами Лобачевского и Римана геометрия Вселенной Евклида была отвергнута.

Еще за триста лет до наступления нашей эры был написан главный труд великого древнегреческого геометра Евклида — «Начала», вершина античной геометрии и античной математики вообще. И два тысячелетия геометрия Евклида была незыблема. Начиная с Галилея наука строила свое великое здание на основе евклидовой геометрии, постулирующей плоское пространство.

В основе геометрии Евклида лежат пять постулатов:

1. От всякой точки до всякой точки можно провести прямую.

2. Ограниченную прямую можно непрерывно продолжать по прямой.

3. Из всякого центра всяким раствором может быть описан круг.

4. Все прямые углы равны между собой.

5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых [1].

Обратите внимание: насколько просты первые четыре постулата, настолько же сложен пятый постулат. Фактически он означает, что через точку, лежащую вне прямой, проходит на плоскости только одна параллельная [1] прямая, а все прочие при своем продолжении данную прямую пересекут.

Сколько существовала геометрия, столько геометры пытались доказать этот постулат, исключить его из списка аксиом и перевести в теорему. Но и самые изощренные математики или допускали ошибку в доказательствах, или приходили к мысли о невыполнимости задачи. Так может быть, пятый постулат недоказуем? Если это так, то значит, он совершенно независим от остальных постулатов — от основ абсолютной геометрии.

Попытки ученых в течение двух тысячелетий, несмотря на отрицательный результат, не были напрасны, ибо в конечном счете привели-таки к полному пересмотру научных представлений о геометрии Вселенной, создав неевклидову геометрию.

Первым математиком, разорвавшим путы евклидовой геометрии, оказался русский ученый Николай Лобачевский.

Он пошел от обратного: предположил, что на плоскости через точку, лежащую вне прямой, можно провести бесчисленное множество прямых, нигде не пересекающих данную прямую [2].

Выдвинув вместо пятого постулата свое допущение, Лобачевский сразу же расстался с привычным евклидовым пространством и открыл существование нового пространства, не похожего на то, в котором мы живем. И в этом пространстве совершенно иной образ принимает плоскость, которую назвали плоскостью Лобачевского.

Давайте в плоскости Евклида (на листе бумаги) начертим прямую [2] линию и точку над ней, а из точки проведем веер прямых, расходящихся в разные стороны. В этой евклидовой плоскости действительно только одна из веера линий, проходящих через точку, будет параллельна исходной прямой.

А теперь мысленно перенесем наш рисунок на плоскость Лобачевского. Это можно сделать только мысленно. Ибо любой перенос линии или геометрической фигуры из евклидова пространства в пространство Лобачевского может быть только условным. Действительно, если на евклидовой плоскости изобразить уже знакомый нам чертеж — исходную прямую, а над ней пучок проходящих через одну точку прямых, но принадлежащих плоскости Лобачевского, то поскольку, согласно постулату Лобачевского, они не должны пересекать исходную прямую, мы вынуждены будем их искривить. И у плоскости Лобачевского появилась кривизна.

Хорошим примером плоскости Лобачевского является особая кривая поверхность, которую называют псевдосферой — она похожа на колпак с загнутыми краями (см. фото на вклейке).

Линии кратчайших расстояний на ней (то есть прямые) будут подчиняться законам Лобачевского, а не Евклида; стороны треугольников в этой плоскости будут зависеть от углов, пятый постулат окажется неверен, и параллельных у данной исходной прямой будет две.

Искривление пространства прямо следует из основного уравнения Лобачевского. В этом уравнении появилась некая постоянная величина, имеющая физический смысл радиуса кривизны. Теоретически этот радиус может иметь разные значения, и каждому из них будет соответствовать свое искривленное пространство.

Кривизна и радиус кривизны — это не одно и то же. Между ними существует обратная связь. Если радиус мал — кривизна велика, радиус велик — кривизна мала. Именно поэтому детский воздушный шарик кажется нам более «круто» искривленным, чем огромный воздушный шар, и уж тем более чем сама Земля. Не случайно в древности нашу планету считали плоской.

А теперь представьте себе океан нашей Вселенной — огромные пространства, по сравнению с которым мала не только Солнечная система, но и наша галактика — Млечный Путь с мириадами звезд. Лобачевский буквально почувствовал, что пространство такой гигантской протяженности может быть не похоже на евклидово пространство относительно небольшого мира, в котором мы живем и который доступен нашим наблюдениям.

Начерченные на бумаге параллельные Лобачевского имеют чисто условный вид. Растяните мысленно этот листок на миллионы и миллиарды световых лет… Поручитесь ли вы, что он не приобретет «по дороге» кривизны? Ведь, не покидая двора своего дома, человек никогда бы не понял, что Земля — это шар. Или сожмите космос до размера листа бумаги.

Лобачевский сумел это сделать. Мощью своего ума, своей фантазией и мечтой Лобачевский покорил пространство и время, он словно предчувствовал свойства безграничных просторов Вселенной.

Заменив своим новым постулатом пятый постулат Евклида и сохранив в неприкосновенности все остальные, Лобачевский построил новую геометрию, геометрию огромных пространств, гигантских межзвездных расстояний, геометрию Вселенной. И пространство Вселенной оказалось искривленным [3].

Если радиус кривизны в уравнении Лобачевского становится равным бесконечности, его пространство становится плоским, переходит в пространство Евклида. Пространство Лобачевского имеет отрицательную кривизну, а поверхность ее вогнута.

Мы с вами живем в мире, размеры которого малы по сравнению со всей Вселенной, а кривизна пространства практически равна нулю, вот мы ее и не замечаем.

Кроме кривизны пространства Лобачевский обнаружил, что геометрия пространства зависит от сил и масс, с которыми тесно связано время.

Что означает зависимость геометрии от сил или от масс? Она означает, что пространство не является абсолютным и однородным. Нет абсолютного, ни от чего не зависящего пространства, одинакового для всех. Нет и абсолютного времени. Пространство и время относительны. Это значит, что размер единицы длины (например, метра) и длительность единицы времени (например, секунды) в подвижной и неподвижной системах отсчета имеют разные величины. Так, на Земле метр имеет одну длину, а на ракете, которая мчится к Марсу — другую. Точно так же обстоит дело со временем: на Земле одно, а на ракете другое. [3].

Высшая духовная Сущность на вопрос оператора «Абсолютны ли пространство и время?» ответила: «Абсолютности в этих понятиях нет. Эти понятия искусственны, так как они выдуманы человеком».

Таким образом, путы, сковывавшие геометрию со времен Евклида, первым разорвал Н. И. Лобачевский.

Величайшим научным подвигом Николая Лобачевского считается создание им первой неевклидовой геометрии, историю которой принято отсчитывать от заседания Отделения физико-математических наук в Казанском университете 11 февраля 1826 года, на котором Лобачевский выступил с докладом «Сжатое изложение основ геометрии со строгим доказательством теоремы о параллельных». Лобачевский не побоялся сделать дерзкий шаг, перед которым из опасения противоречий останавливались его предшественники: построить геометрию, противоречащую повседневному опыту и «здравому смыслу» — квинтэссенции повседневного опыта. И поплатился за это. Современники его не поняли и не приняли его научные идеи.

Декан физико-математического факультета (а с 1827 года — и ректор Казанского университета), прекрасный преподаватель и великий ученый, он много сделал для развития университета. Однако новое начальство лишило его кафедры и профессорского звания, и некоторое время свои обязанности ректора Казанского университета Лобачевский продолжал исполнять, не получая никакого вознаграждения. Как сказали бы в советские времена, «работал на общественных началах». Его не стало 12 февраля 1856 года, ровно через тридцать лет после памятного дня, когда родилась геометрия Лобачевского. И за все тридцать лет ему не повезло встретить единомышленника, разделившего бы с ним взгляды на пространство!

Пространство Лобачевского есть пространство трех измерений, отличающееся от нашего тем, что в нем нет места пятому постулату Евклида [3].

На вопрос оператора «Трехмерен ли мир?» Высшая духовная Сущность ответила: «Мир многомерен. Понятие трех изменений — это представление людей. Вспомним голографию. Возьмем любой предмет, хотя бы куб, и представим его голограмму, но не со стороны, а как бы войдя внутрь ее». А на вопрос «Как можно представить четвертое и пятое измерения?» был получен ответ: «Возьмите матрешку, посмотрите на нее со стороны верхнего слоя, а затем представьте первый слой прозрачным и т. д. Но это взгляд с одного ракурса. То же можно сделать и со стороны верхней части, и со стороны донца».

Бернхард Риман родился в 1826 году, как раз в тот год, когда Лобачевский в Казани обнародовал свою геометрию. Кстати, Ньютон родился в год смерти Галилея. А Эйнштейн — в год смерти Максвелла.

Риман, который, как оказалось, не был знаком с трудами Лобачевского, создал огромный, неизвестный ранее человечеству мир математических пространств, или, по его терминологии, многократно протяженных многообразий, и каждое из них должно было обладать своей собственной геометрией.

Потребовалось установить строение каждого пространства, то есть найти геометрию, ему присущую, научиться строить в нем фигуры и измерять их, иными словами, требовалось установить метрику. Риман предложил общий универсальный принцип: метрические отношения следует искать и фиксировать в бесконечно малой области пространства. Проще говоря, пространство надо мерить бесконечно малыми шагами. Именно в бесконечно малой области действуют более простые законы и более явственно обнажается суть явления и его особенности, характерные для данного момента времени и данной точки пространства [4].

Риман был убежден, что для всех явлений природы, в том числе и для тяготения, взаимодействие на больших расстояниях должно быть следствием микровзаимодействий, то есть процессов, протекающих в соседних бесконечно малых элементах пространства.

Точно суть работы Римана выразил советский геометр Каган, сказав: «Риман расщепил пространство на бесконечно малые элементы и показал, как из упрощенной метрики элемента разворачивается метрика всего пространства».

Выиграв в широте охвата, в общности подхода, Риман проиграл в содержании — им даны основные идеи, но детальной их проработки нет. У Лобачевского было наоборот. Он оставил нам глубокую и детальную проработку своей геометрии.

Позднее Риман решил «спуститься» к некоторым конкретным геометриям — наиболее простым, хотя на примере Лобачевского мы знаем, что простота может быть весьма относительной. Из всего этого многообразия Риман выделил простейшие многообразия — с постоянной кривизной.

Самый простой случай — когда кривизна всюду равна нулю. В одном измерении — это прямая линия, в двух — плоскость, в трех — евклидово пространство. Но кривизна может быть отличной от нуля, хотя и постоянна.

Раз кривизна постоянна, она, естественно, может быть нулевой, постоянно отрицательной и постоянно положительной.

В первом случае речь идет о пространстве Евклида, во втором — о пространстве Лобачевского, а в третьем случае при одинаково положительной кривизне — о пространстве Римана.

Причем третья постоянная положительная кривизна — это полная собственность Римана. Поэтому геометрия пространства с такой кривизной называется геометрией Римана.

В известном смысле мы достаточно часто сталкиваемся с постоянной положительной кривизной, правда, с кривизной поверхности, а не пространства. Любые шары есть поверхности постоянной положительной кривизны. Тем не менее, нам трудно вообразить себе сферическое пространство. Мир Евклида, трехмерное пространство нулевой кривизны, входит в нас при рождении.

Чтобы познакомиться с пространством Римана (с пространством постоянно положительной кривизны), возьмем в руки глобус, но отвлечемся от физической географии планеты, оставив только сетку меридианов и параллелей. Сфера — это пространство с постоянной положительной кривизной. Что представляет собой прямая линия на сфере? Если понимать прямую линию как линию нулевой кривизны, то на сфере прямых нет; любая изогнута, любая имеет кривизну. Но если прямая — это кратчайшее расстояние между двумя точками, то дело обстоит иначе. На сфере прямая — это часть дуги.

Следовательно, все меридианы — это прямые на сфере. И экватор тоже. Параллели определению прямых не отвечают, ибо длина их дуг больше кратчайшего расстояния между двумя точками, то есть между концами этих же дуг.

Сферическое пространство, или пространство постоянной положительной кривизны, замкнуто и конечно (от слова «конец»), также как замкнут и конечен шар. Таким же свойством обладает и другое пространство положительной кривизны — эллиптическое. (Как окружность есть частный и предельный случай эллипса, так и шар есть частный и предельный случай эллипсоида. Поэтому эллиптическая поверхность, а равно и эллиптическое пространство, есть обобщение сферических поверхности и пространства.)

Замкнутость и конечность пространства Римана нанесли удар по укоренившимся представлениям о бесконечности пространства.

Риман понял, что слова «безграничность» и «бесконечность» имеют разный смысл. Безграничность — значит без границ! А бесконечность — это то, что простирается без конца. Это расстояние, которое хотя и измеряемо, но в принципе не может быть измерено до конца, потому что конца просто нет.

Он утверждал: «При рассмотрении пространственных построений в направлении неизмеримо большого, следует различать свойства ограниченности и бесконечности — первое из них есть свойство протяженности, второе — метрическое свойство»[4].

Чрезвычайно важен физический смысл, но еще более важен философский смысл этого открытия. Ведь философы были убеждены, что бесконечность и безграничность — синонимы.

Риман говорил: «То, что пространство есть неограниченное трижды протяженное многообразие [3] , является допущением, принимаемым в любой концепции внешнего мира. Но отсюда никоим образом не следует бесконечность пространства: напротив, если припишем пространству постоянную меру кривизны, то придется допустить конечность пространства, как бы мала ни была мера кривизны, лишь бы она была положительной» [4].

Именно безграничное, но конечное пространство положит А. Эйнштейн в основу своей теории относительности.

А как обстоят дела с параллельными прямыми в пространстве Римана? Оказывается, параллельных в геометрии Римана нет. Ибо меридианы, которые являются прямыми, обязательно пересекаются, и даже в двух точках.

Таким образом, в плоскости Евклида всегда есть одна прямая, параллельная исходной, в плоскости Лобачевского — две, а в плоскости Римана их нет вообще. Интересна также ситуация с углами. Если у Лобачевского сумма углов треугольника меньше суммы двух прямых, у Евклида — равна сумме двух прямых, то у Римана — больше суммы двух прямых. По этим показателям геометрия Евклида оказалась промежуточной между геометрией Лобачевского и Римана.

Отметим, что геометрия Римана называется еще «эллиптической», геометрия Лобачевского — гиперболической, а геометрию Эвклида называют плоской.

Работу по развитию неевклидовой геометрии продолжил целый ряд ученых, подхвативших идеи Лобачевского и Римана.

Очень урожайным оказался 1868 год. В печати одна за другой стали появляться статьи о неевклидовой геометрии. Это были работы итальянского математика Э. Бельтрама, поразительные статьи Гельмгольца, и, наконец, была опубликована переписка великого Гаусса с друзьями, поскольку обет молчания после его смерти закончился. Из переписки следовало, что Гаусс и сам упорно занимался неевклидовой геометрией, высоко оценивал работы Лобачевского, но при жизни промолчал и не поддержал открыто русского ученого, подвергавшегося осмеянию и гонениям.

С 1868 года началось массовое признание новых идей неевклидовой геометрии. Отныне она становится одной из магистральных дорог в математике. Продолжили работу блестящий ученый конца XIX века профессор Геттингенского университета Давид Гильберт, замечательный российский математик Александр Фридман, блестящий английский математик Уильям Клиффорд и т. д.

Таким образом, к концу XIX века неевклидова геометрия буквально выбила из-под классической физики одну из трех опор, на которых та базировалась. И при этом было совершенно неясно, что делать дальше с эфиром, как переносчиком взаимодействий.

Неясна была и ситуация с принципом относительности Галилея, который был справедлив для механических явлений. Во всех инерциальных системах (то есть движущихся прямолинейно и равномерно по отношению друг к другу) применимы одни и те же законы механики. Но справедлив ли этот принцип для немеханических явлений, особенно для тех, которые связаны с электромагнитными явлениями?

Ответы на эти вопросы связаны с изучением взаимосвязи движущихся тел с эфиром, но не как с механической средой, а как со средой-носителем электромагнитных колебаний. Требовалось ответить на вопросы: как взаимодействуют весомые тела и эфир (полагали, что эфир проникает в тела); отличается ли эфир внутри тела от находящегося вовне; как ведет себя эфир внутри тел при их движении и т. д. А доказательств существования эфира по-прежнему не было. Как можно определить свойства неизвестно чего?

Для дальнейшего развития теоретической физики нужна была теория, которая могла бы разрешить очередной сложившийся кризис. Долгое время попытки ученых в этом вопросе были тщетны, и лишь спустя почти четверть века после первого опыта Майкельсона выход из создавшегося положения в 1905 году предложил молодой Альберт Эйнштейн, опубликовав свою первую работу по теории относительности «К электродинамике движущихся тел».

Анализируя результаты опытов Физо и Майкельсона, Эйнштейн в своей работе приходит к выводу, что следует отказаться от введения понятия «эфир», так как предположение о том, что эфир покоится одновременно в двух системах (в системе, связанной с Землей, в опыте Майкельсона и в неподвижной системе в опыте Физо), является абсурдным.

В свое время опыт Физо был объяснен наличием мирового неподвижного эфира, в котором движутся все тела. Опыт Майкельсона опроверг эту гипотезу: скорость света относительно Земли всегда имела одно и то же значение независимо от того, движется Земля в направлении движения луча света или навстречу этому лучу. Это можно было бы объяснить движением Земли вместе с околоземным эфиром, в котором распространяется луч света. О возможности такого объяснения говорит и Эйнштейн, но тогда становится непонятным опыт Физо, показавший, что тело не движется вместе с эфиром.

Как было установлено наукой много позднее, перемещающееся на Земле тело в опыте Физо действительно не движется вместе с эфиром внутри тела, так как этот эфир удерживается силой гравитации Земли.

Однако Эйнштейн приходит к отказу от эфира не только на основании анализа опытов Физо и Майкельсона, но и в результате анализа всей истории развития физики, показанной в великолепно написанной книге «Эволюция физики».

Не найдя механического объяснения эфира, Эйнштейн выносит ему смертный приговор: «Все наши попытки сделать эфир реальным провалились. Он не обнаружил ни своего механического строения, ни абсолютного движения. Все попытки открыть свойства эфира привели к трудностям и противоречиям. После стольких неудач наступает момент, когда следует совершенно забыть об эфире и постараться никогда больше не упоминать о нем» [5].

Кроме того, в этой работе было показано, что никакого эфира не нужно, если отказаться от понятия абсолютного времени.

Предложение Эйнштейна охотно подхватило большинство физиков, поскольку безуспешность многочисленных попыток примирить между собой противоречивые свойства эфира и разработать приемлемую его теорию была просто удручающей. Эфир достал буквально всех! А так «нет объекта — нет проблемы».

Налицо кризис в физике: эфир отвергнут, пространство неевклидово и не абсолютно, как и время.

Все это указывало на необходимость смены парадигмы в естествознании. А смена парадигмы [4] — это настоящая научная революция.

Парадигма, господствующая в науке, служит эталоном, с помощью которого отбираются, оцениваются и критикуются факты, идеи и теории. Словом, парадигма в науке — это что-то вроде прокрустова ложа. Помните, знаменитый разбойник Прокруст хватал путников на большой дороге, укладывал их на некую кровать, и коротких вытягивал «до нормы», а длинных обрубал до размеров кровати.

Зато при наличии парадигмы ученым при изучении различных явлений уже не приходится каждый раз начинать все с самого начала — с формулировки основных принципов. И приняв на веру парадигму, они могут сосредоточиться на решении конкретных головоломок.

Но со временем, по мере накопления знаний, парадигма устаревает и начинает тормозить развитие науки. Возникает кризис, который неизбежно завершается сменой научной парадигмы.

Вот такая ситуация и создалась в науке в конце XIX — начале XX века. Была необходима новая научная парадигма. А какая? Кто ж ее знает!

И вот в такой ситуации Эйнштейн взялся за разработку новой теории, которая помогла бы выйти из затянувшегося кризиса и послужила бы основой для дальнейшего развития теоретической физики.

Все просто, когда уже найдено. И как неимоверно сложно, когда неизвестно, где именно искать.

Но Эйнштейн не был бы Эйнштейном, если бы ничего не придумал.

И он придумал теорию относительности, да не одну, а две. Специальную и общую. По выражению Эйнштейна, его теория относительности представляет собой «дом с двумя этажами».

Специальная теория относительности

Многие из нас знают о теории относительности понаслышке и считают, что это что-то туманное и очень сложное.

По поводу этой теории существует шутливое стихотворение, автор которого, к сожалению, нам не известен:

Был мир земной кромешной тьмой окутан,

Да будет свет! И вот явился Ньютон!

Но сатана недолго ждал реванша:

Но не так страшен черт, как его малюют. Не вдаваясь в математику, давайте познакомимся с сутью теории относительности Эйнштейна, которая на многие годы определила путь развития науки.

Итак, в 1905 году Эйнштейн опубликовал ряд работ, которые содержали три радикально новые идеи. Первая, которую мы уже вспоминали, полностью отвергала эфир; вторая стала основой специальной теории относительности; третья заставила по-новому взглянуть на электромагнитное излучение и легла в основу теории атома — квантовой теории, которая в окончательном виде сформировалась через двадцать лет благодаря совместным усилиям целой группы физиков.

Однако теорию относительности практически полностью разработал сам Эйнштейн. Она состоит из двух частей: специальной теории относительности (СТО), рассматривающей релятивистские явления (то есть явления, проявляющиеся при движении тел со скоростями, близкими скорости света), и общей теории относительности (ОТО), распространяющей положения СТО на гравитационные явления.

В основе как той, так и другой теории лежат постулаты — положения, принимаемые без доказательств, на веру. В геометрии такие положения называются аксиомами.

Принято считать, что в основе СТО лежат два постулата.

В качестве первого постулата Эйнштейн использовал принцип относительности Галилея, который в современной обработке гласит: «Во всех инерциальных системах отсчета законы классической динамики имеют один и тот же вид» [6].

Что интересно: этот постулат был бы невозможен при существовании эфира. Пришлось бы рассматривать движение тел относительно него. А раз эфира нет, то и рассматривать нечего.

Вторым постулатом является принцип постоянства скорости света. Эйнштейн поставил свет в особое положение, сформулировав этот принцип так: «Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета» [7].

По поводу постулатов, лежащих в основе специальной теории относительности, есть и другое мнение: в основе этой теории лежат не два, а пять постулатов [8].

«Первым постулатом является положение об отсутствии эфира, ибо, как утверждал сам Эйнштейн, „нельзя создать удовлетворительную теорию, не отказавшись от существования некой среды, заполняющей все пространство“. Уж не потому ли и был отвергнут эфир, что он не вписывался в новую теорию Эйнштейна?

Вторым постулатом является принцип относительности Галилея. Что интересно: этот постулат был бы невозможен при существовании эфира. Пришлось бы рассматривать движение тел относительно эфира. А раз эфира нет, то и рассматривать нечего.

Третьим постулатом является принцип постоянства скорости света.

Четвертым постулатом является инвариантность (неизменность) интервала, состоящего из четырех составляющих — трех пространственных координат и времени, умноженного на скорость света. Почему на скорость света? А ни почему. Постулат! А постулаты не требуют доказательств.

Пятым постулатом является „принцип одновременности“, согласно которому факт одновременности двух событий определяется по моменту прихода к наблюдателю светового сигнала. Почему светового сигнала, а не звука, не механического движения, не телепатии, наконец? Тоже ни почему. Постулат!» [8]. А постулаты не требуют доказательств.

Из этого простого принципа вытекает ряд замечательных следствий. Самые известные из них — это эквивалентность массы и энергии, нашедшая свое выражение в знаменитом уравнении Эйнштейна E = mc2 (где E — энергия, m — масса, c — скорость света), и закон, согласно которому ничто не может двигаться быстрее света.

Стоит отметить, что к настоящему времени получены экспериментальные данные, свидетельствующие о существовании скорости, большей скорости света.

Проблема заключалась в том, что два постулата, которые Эйнштейн положил в основу СТО, несовместимы, поскольку, согласно принципу относительности Галилея, один и тот же луч света не может иметь одну и ту же скорость относительно наблюдателей, движущихся относительно друг друга [9].

Эйнштейн ищет выход из создавшегося положения и находит его в пересмотре важнейших положений классической физики — абсолютности пространства и времени.

Опираясь на геометрию Лобачевского и Римана, Эйнштейн вводит понятия относительности пространства и времени. В работе «Что такое теория относительности?» Эйнштейн отмечает, что принципы относительности и постоянства скорости света являются непримиримыми, но «специальная теория относительности сумела их примирить ценой видоизменения кинематики, иначе говоря, ценой изменения физических представлений о пространстве и времени» [10].

Итак, обосновав новую кинематику, базирующуюся на относительности пространства и времени, Эйнштейн сумел выдвинутый им закон постоянства скорости света подчинить принципу относительности.

По теории Ньютона, если световой импульс послан из одной точки в другую, то время его прохождения, измеренное разными наблюдателями, будет одинаковым (поскольку время абсолютно), но пройденный путь может быть разным (поскольку пространство не абсолютно). Разные наблюдатели будут получать разную скорость света.

В СТО скорость света для всех наблюдателей одинакова. Время прохождения, то есть пройденное светом расстояние, деленное на постоянную скорость света, окажется разным для разных наблюдателей. Оказалось, что у каждого наблюдателя должен быть свой масштаб времени. Теория относительности покончила с понятием абсолютного времени, исключив возможность существования сил дальнодействия. Это важнейшее из открытий Эйнштейна.

Однако время не отделено от пространства.

Нам с вами в нашем мире для определения положения точки в пространстве необходимы три координаты: X, Y, Z. Объединение пространства и времени в единый пространственно-временной континуум означало перевод всех физических процессов в четырехмерное пространство-время и потребовало введение четвертой координаты. Этой координатой стало время ct, где с — скорость света в пустоте (с = 300 000 км/с); t — время.

Надо сказать, что все замечательные математические открытия Эйнштейна о зависимости массы тела, его длины, времени, энергии импульса и т. д. от скорости света выведены на основе преобразований Лоренца. Правда, эти преобразования Лоренц вывел еще в 1904 году, за год до создания СТО, и вывел их из представления о существовании в пространстве неподвижного эфира, который был отвергнут Эйнштейном [8].

Нам труднее всего понять относительность пространства и времени. Изменение пространства в движущейся системе проявляется в сокращении размеров тел, движущихся в направлении движения. И чем больше скорость, тем больше сокращение.

То же самое происходит со временем. Время затормаживается в движущейся системе. Изменение времени проявится в изменении частоты всех периодических процессов; например, если из неподвижной системы измерять ход часов в системе движущейся, то окажется, что этот ход будет замедленным; или частота колебаний атомов и молекул, измеренная таким же образом, будет меньше, чем в «своей», неподвижной системе.

Возникает вопрос: почему же ученые не обнаружили этого раньше? Эйнштейн объяснил это тем, что эффекты, которыми «ведает» теория относительности, становятся заметны только при очень больших скоростях, сравнимых со скоростью света. Но даже скорости спутников, как они не велики, все-таки в тридцать-сорок тысяч раз меньше световой.

Другое дело, когда изучаются космические лучи или рассчитываются ускорители, в которых заряженные частицы разгоняются почти до скорости света — тогда без теории относительности невозможно сделать ни одного расчета.

А в обычных условиях, в мире малых скоростей, законы Эйнштейна переходят в законы классической механики Ньютона. Макс Планк, с чьим именем связано создание квантовой механики, писал: «По своей глубине и последствиям переворот, вызванный принципом относительности в сфере физических воззрений, можно сравнить только с тем переворотом, который был произведен введением картины мироздания, созданной Коперником» [4].

Понятия времени и пространства настолько основополагающи, что их изменение влечет за собой изменение общего подхода к описанию явлений природы. Одним из важных последствий этого изменения явилось осознание того, что масса — это одна из форм энергии. Никто и никогда даже представить себе не мог, что масса — это энергия!

Это открытие позволило сделать далеко идущие выводы. Так, индийский мыслитель Шри Ауробиндо утверждает: «Формула Эйнштейна — поистине великое открытие — говорит нам, что Материя и Энергия взаимозаменяемы: E = mc2. Материя — это сгущенная Энергия. Теперь мы должны убедиться на опыте, что эта Энергия есть Сознание, и что Материя — это тоже форма сознания, точно так же как Разум — форма сознания. Если бы хоть одна точка Вселенной была бы лишена сознания, то вся Вселенная была бы лишена его, потому что бытие должно быть единым» [11].

Хотя геометрические свойства пространства-времени описываются геометрией Евклида, все равно чрезвычайно трудно понять четырехмерное пространство-время, которое еще называют миром Минковского — Эйнштейна.

Появление имени Германа Минковского не случайно, ибо он также пришел к выводу об абсолютности четырехмерного пространства-времени. В 1908 году он на собрании естествоиспытателей и врачей в Кельне прочел исторический доклад «Пространство и время», о геометрических основах теории относительности. Начинался доклад так: «Воззрения на пространство и время, которые я намерен перед вами развить, возникли на экспериментально-физической основе».

Надо сказать, что Эйнштейн, будучи студентом Федерального высшего политехнического училища в Цюрихе, посещал лекции Минковского и был у него не на лучшем счету. Поэтому когда появилась теория относительности, Минковский был поражен не только ее содержанием, смелостью и глубиной, но и тем, что ее автором оказался далеко не самый блестящий его студент. Он говорил Максу Борну: «Это было для меня огромной неожиданностью. Ведь раньше Эйнштейн был настоящим лентяем. Математикой он не занимался вовсе» [4].

По поводу сложности понимания четырехмерного пространства-времени Эйнштейн писал: «Представьте себе совершенно сплющенного клопа, живущего на поверхности шара. Этот клоп может быть наделен аналитическим умом, может изучать физику и даже писать книги. Его мир будет двухмерным. Мысленно или математически он даже сможет понять, что такое третье измерение, но представить его себе наглядно он не сможет. Человек находится в таком же положении, что и этот несчастный клоп, с той лишь разницей, что человек трехмерен. Математически человек может вообразить себе четвертое измерение, но представить его не может. Для него четвертое измерение существует лишь математически. Разум его не может постичь четырехмерия».

Но Эйнштейн-то смог!

Благодарим за внимание.

1. Начала Евклида // http://ru.wikipedia.org/wiki/

2. Лобачевский Н. И. // http://ru.wikipedia.org/wiki/

3. Лобачевский Н. И. // http://to-name.ru/biography/nikolaj-lobachevskij.htm

4. Ливанова А. Три судьбы постижения мира. Жизнь замечательных идей. М.: Знание, 1969.

5. Брусин Л. Д., Брусин С. Д. Иллюзия Эйнштейна и реальность Ньютона. М.: 1994.

6. Принцип относительности Галилея http://space.rin.ru/articles/html/422.html

7. Физический энциклопедический словарь. М.: Советская энциклопедия, 1984.

8. Ацюковский В. А. Популярная эфиродинамика, или Мир, в котором мы живем. М.: Знание, 2006.

9. Тихоплав В. Ю., Тихоплав Т. С. Физика веры. СПб.: Весь, 2005.

10. Яворский Б. М., Детлеф А. А. Справочник по физике. М.: Наука, 1985.

11. Сатпрем. Шри Ауробиндо, или Путешествие сознания. Л.: Изд-во ЛГУ, 1989.

Источник

Геометрия пространства геометрия вселенной