Глобальная волновая функция вселенной формула

Волновая функция Вселенной

Хокинг — один из основоположников новой научной дисциплины, называемой квантовой космологией. Поначалу терминология казалась противоречивой. Слово квант относится к бесконечно малому миру кварков и нейтрино, а космология ассоциируется с почти бесконечным космическим пространством. Однако Хокинг и его последователи убеждены, что на основные вопросы космологии можно ответить только с помощью квантовой теории. Хокинг подводит квантовую космологию к окончательному квантовому заключению, допуская существование бесконечного множества параллельных вселенных.

Как мы помним, отправная точка квантовой теории — волновая функция, описывающая все возможные состояния частицы. К примеру, представим себе огромную грозовую тучу неправильной формы, заволакивающую небо. Чем темнее туча, тем выше концентрация водяного пара и пыли в этой точке. Таким образом, достаточно просто взглянуть на тучу, чтобы оценить вероятность обнаружения высокой концентрации воды и пыли в определенных местах на небе.

Эту тучу можно сравнить с волновой функцией единственного электрона. Подобно грозовой туче, она заполняет все пространство. Чем больше ее величина в какой-либо точке, тем выше вероятность обнаружить там электрон. Аналогичным образом волновая функция может ассоциироваться с крупными объектами, например людьми. Сидя в кресле у себя в Принстоне, я знаю, что обладаю шрёдингеровской вероятностной волновой функцией. Если бы мне как-нибудь Удалось увидеть собственную волновую функцию, она напомнила бы мне облако в форме моего тела. Однако часть этого облака распространилась бы по всему пространству вплоть До Марса и даже за пределы Солнечной системы, хотя была бы в этом случае исчезающе малой. Это означает, что вероятность моего пребывания в кресле, а не на планете Марс, довольно велика. Несмотря на то что отчасти моя волновая функция распространилась за пределы галактики Млечный Путь, вероятность того, что я сижу в другой галактике, бесконечно мала.

Новая идея Хокинга заключалась в том, чтобы воспринимать вселенную в целом так, словно она представляет собой квантовую частицу. Повторив несколько простых шагов, мы придем к выводу, который откроет нам глаза.

Начнем с волновой функции, описывающей совокупность всех возможных вселенных. Это означает, что отправной точкой теории Хокинга должен быть бесконечный ряд параллельных вселенных — волновая функция Вселенной. Довольно простой анализ Хокинга, в котором слово частица заменено словом Вселенная, привел к перевороту в наших представлениях о космологии.

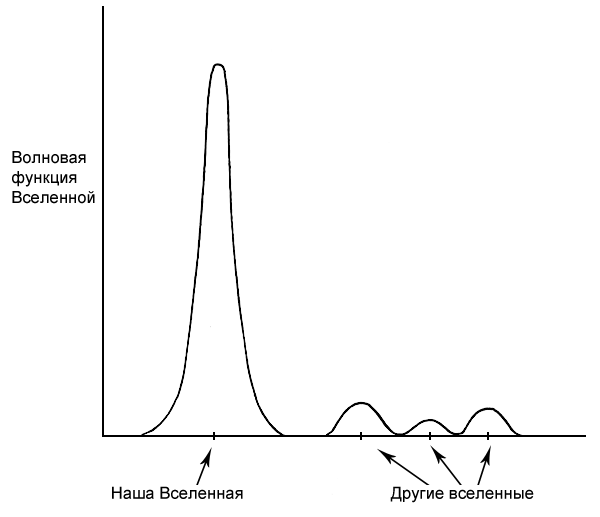
Согласно этой картине волновая функция Вселенной распространяется во всех возможных вселенных. Подразумевается, что эта волновая функция довольно велика вблизи нашей Вселенной, следовательно, есть немалая вероятность, что наша Вселенная и есть та, которая нам нужна, чего и следовало ожидать. Но волновая функция распространяется и на все остальные вселенные, в том числе безжизненные и несовместимые с привычными нам законами физики. Поскольку волновая функция предполагается для этих прочих вселенных исчезающе малой, мы не рассчитываем, что наша Вселенная сделает квантовый скачок к ним в ближайшем будущем.

Цель, стоящая перед квантовыми космологами, — подтвердить эту догадку математически, показать, что волновая функция Вселенной велика для нашей нынешней Вселенной и исчезающе мала для остальных. Это доказывало бы, что привычная для нас Вселенная в некотором смысле уникальна и вместе с тем стабильна. (В настоящее время специалисты по квантовой космологии не в силах решить эту важную задачу.)

Если отнестись к доводам Хокинга со всей серьезностью, это означает, что начать анализ следует с бесконечного количества всех возможных вселенных, сосуществующих друг с другом. Или, попросту говоря, определение Вселенной теперь не сводится к выражению «все, что существует». Теперь это означает «все, что может существовать». Например, на рис. 12.1 мы видим, как волновая функция Вселенной может распространиться на несколько возможных вселенных, причем наша окажется наиболее вероятной, но определенно не единственной. Квантовая космология Хокинга также подразумевает, что волновая функция Вселенной позволяет этим вселенным сталкиваться. «Червоточины» могут возникать и соединять эти вселенные. Однако это не те «червоточины», с которыми мы имели дело в предыдущих главах, не те, которые соединяют разные области трехмерного пространства: в данном случае «червоточины» соединяют друг с другом разные вселенные.

Рис. 12.1. Волновая функция вселенной Хокинга с наибольшей вероятностью сосредоточена вокруг нашей Вселенной. Мы живем в нашей Вселенной, поскольку это наиболее подходящий и наиболее вероятный вариант. Однако есть маленькая, но не исчезающая вероятность, что волновая функция предпочитает соседние, параллельные вселенные. Таким образом, переходы между вселенными возможны (хотя и очень маловероятны).

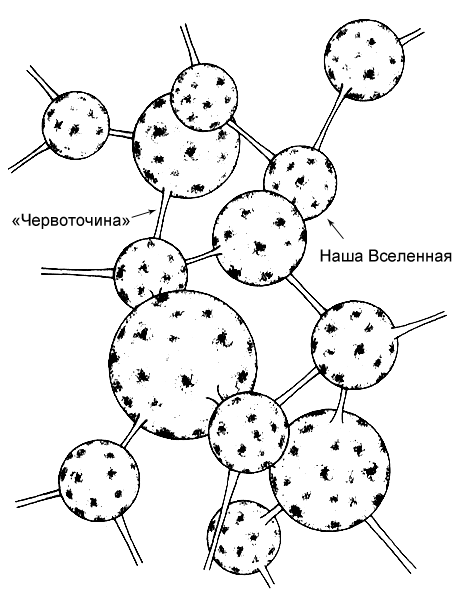
Представим себе, к примеру, множество мыльных пузырей, зависших в воздухе. При нормальных условиях каждый такой пузырь представляет собой вселенную, он периодически сталкивается с другими пузырями и сливается в один большой или делится на два пузыря поменьше. Отличие в том, что теперь каждый мыльный пузырь — целая десятимерная вселенная. Так как пространство и время могут существовать только на каждом пузыре, между ними нет ни пространства, ни времени. У каждой вселенной свое «время», ограниченное ею одной. Незачем добавлять, что время во всех этих вселенных идет с одинаковой скоростью. (Однако следует подчеркнуть, что путешествия между вселенными недоступны для нас из-за примитивного уровня развития нашей техники и технологии. Более того, необходимо отметить, что большие квантовые переходы в таких масштабах крайне редки, их частота сопоставима с продолжительностью существования нашей Вселенной.) Большинство таких вселенных мертвы, полностью лишены признаков жизни. В этих вселенных действуют другие законы физики, следовательно, физические условия, благодаря которым жизнь стала возможной, не сложились. Может быть, среди миллиардов параллельных миров только один, наш, обладает тем набором физических законов, который нужен для появления жизни (рис. 12.2).

Рис. 12.2. Наша Вселенная может оказаться одним из бесчисленного множества параллельных миров, каждый из которых связан с остальными бесконечным множеством «червоточин». Путешествия по этим «червоточинам» возможны, но чрезвычайно маловероятны.

Теория «дочерней вселенной» Хокинга хотя и не предлагает практические методы транспортировки, тем не менее поднимает философские и, возможно, даже религиозные вопросы. Она уже породила два затяжных спора в кругах космологов.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Глобальная волновая функция вселенной формула

Экспериментальное подтверждение идеи Луи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также противоречия ряда экспериментов с применяемыми в начале XX века теориями привели к новому этапу развития квантовой физики – созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств. Ее создание и развитие охватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20-х годов XX века и связано, прежде всего, с работами австрийского физика Э. Шредингера, немецкого физика В. Гейзенберга и английского физика П. Дирака.

Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Можно ли волны де Бройля истолковывать как волны вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно, хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.

Чтобы устранить эти трудности, немецкий физик М. Борн в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая . Эту величину называют также волновой функцией (или -функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:

где , где – функция комплексно-сопряженная с Ψ.

Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волны де Бройля) определяет вероятность нахождения частицы в момент времени в области с координатами x и dx, y и dy, z и dz.

Итак, в квантовой механике состояние частицы описывается принципиально по-новому – с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых

Величина (квадрат модуля Ψ-функции) имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единице объема в окрестности точки, имеющей координаты x, y, z. Таким образом, физический смысл имеет не сама Ψ-функция, а квадрат ее модуля , которым определяется интенсивность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме о сложении вероятностей, равна:

Т.к. определяется как вероятность, то необходимо волновую функцию Ψ представить так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей:

где данный интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от до . Таким образом, условие нормировки говорит об объективном существовании частицы во времени и пространстве.

Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять ряду ограничительных условий. Функция Ψ, характеризующая вероятность обнаружения микрочастицы в элементе объема, должна быть:

· конечной (вероятность не может быть больше единицы);

· однозначной (вероятность не может быть неоднозначной величиной);

· непрерывной (вероятность не может меняться скачком).

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями , , … , то она может находиться в состоянии, описываемом линейной комбинацией этих функций:

где (n = 1, 2, 3…) – произвольные, вообще говоря, комплексные числа.

Сложение волновых функций (амплитуд вероятностей, определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.

Волновая функция Ψ является основной характеристикой состояния микрообъектов. Например, среднее расстояние электрона от ядра вычисляется по формуле

где вычисления проводятся, как и в случае (4.3.3).

Источник

Глобальная волновая функция вселенной формула

Волновая функция Вселенной

Читайте также

Глава VIII. Волновая механика

Глава XII. Волновая механика систем и принцип Паули

1. Волновая механика систем частиц

Волновая теория света

53. Волновая оптика

МАСШТАБЫ ВСЕЛЕННОЙ

ГЛАВА 1 ВОЛНОВАЯ И КОРПУСКУЛЯРНАЯ ТЕОРИИ СВЕТА

Волновая теория со временем становится доминирующей

2. Вкратце о Вселенной

Глобальная волновая функция вселенной формула