Гравитационная неустойчивость во вселенной
Возникновение звезд и других небесных тел возможно только потому, что в мире существует гравитация. Об этом, писал еще Ньютон в письме к Бентли в 1692 г. Идея Ньютона была оформлена физически и математически Джинсом в его известной книге «Астрономия и космогония» [10]. Сущность механизма Ньютона-Джинса, или механизма гравитационной неустойчивости, заключается в следующем.
Во всяком газе всегда имеются флуктуации плотности, возникающие при хаотическом, движении составляющих газ атомов или молекул. Эти флуктуации воникают и распадаются, причем динамика флуктуации определяется одним параметром — температурой.
Ситуация существенно изменится, если мы, кроме температуры, рассмотрим, другой фактор — тяготение. Для малых масштабов гравитация не существенна. Для больших масштабов может случиться, что собственное притяжение такой флуктуации окажется способные удержать газ в данном объеме и не дать ему рассеяться. Сила тяготения нарастает с увеличением массы, а тепловые свойства среды не зависят от размера. В этих условиях возможно разбиение первоначально однородной среды на сгустки с некоторым характерным масштабом, называемым джинсовской длиной.
Оценку джинсовской, или критической, длины можно сделать следующим образом. Сравним тепловую энергию сгущения (флуктуации) с его гравитационной энергией. Гравитационная энергия на единицу массы
 | (8.12) |
где λ — характерный размер сгущения. Тепловая энергия на единицу массы есть
 | (8.13) |
Приравнивая эти две величины, получим выражение для критической длины волны
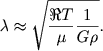 | (8.14) |
Можно получить формулу Джинса и из соображений размерности. Определяющие параметры задачи таковы. Гравитационные свойства среды задаются средней плотностью ρ и постоянной тяготения G. Тепловые свойства зависят от температуры, универсальной газовой постоянной и молекулярного веса. Эти факторы мы сгруппируем вместе. Тогда имеем матрицу размерности:
 |
Решение матрицы дает единственный безразмерный комплекс, также приводящий к формуле (8.14) с точностью до некоторого безразмерного множителя. Обычно выражают температуру через изотермическую скорость звука:
 | (8.15) |
Безразмерная постоянная равна π ½ , и мы получаем, формулу Джинса в ее обычном виде:
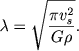 | (8.16) |
Понятие гравитационной неустойчивости имеет простой физический смысл. Устойчивость любой системы проверяется наложением на систему малых колебаний. Если колебания затухают, система устойчива, если они начинают расти — неустойчива. Ввиду наличия гравитации колебания газа в больших масштабах называют «тяжелым звуком» (см. гл. 7). Колебания с меньшей длиной волны затухают, так как в них тепловая энергия больше гравитационной; колебания с большей длиной волны — неустойчивы. Переход среды из устойчивого состояния в неустойчивое легко понять, если вспомнить, что при малых плотностях космический газ почти всегда прозрачен. При постепенном остывании температура понижается и среда становится гравитационно неустойчивой.
В соотношениях (8.14) — (8.16) не рассматривается динамика распада на сгущения, а находится только критерии гравитационной неустойчивости, строго справедливые для случая, когда исходная среда в начальный момент времени покоится. Такая важная для космологии задача, как распад на сгущения расширяющейся среды, была решена впервые Е. М. Лифшицем (подробности см. [2]), который учел зависимость начальной плотности от времени. Впрочем, оказалось, что результаты Джинса с очень небольшими поправками остаются справедливыми и в этом случае, если принимать для 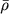
Теперь проследим дальнейшую судьбу гравитационных конфигураций. Массы конденсаций, «образующихся в тяжелом звуке, порядка
 | (8.17) |
где vs — характерная скорость. В простейшем случае это скорость звука, но вообще она может отражать и наличие других факторов (вращение, турбулентность, скорость альвеновоких волн). Минимальное значение М определяется газовым и лучистым давлением. Поэтому минимальная масса конденсаций
 | (8.18) |
В настоящее время минимальная температура космической среды равна 3њ. В прошлом температуры были выше. В зависимости от хода изменения плотности и температуры для конкретных моделей, массы образующихся конденсаций оказываются различными. Конденсации в волнах «тяжелого звука» собирают вещество, оставшееся вне сгущения. Характерное время такого собирания можно оценить, подставляя в формулу аккреции (2.30) вместо массы звезды массу образовавшихся сгущений (8.17). Тогда для относительного изменения массы имеем
Характерное время здесь сравнимо (несколько меньше) со временем, свободного падения. Таким образом, образовавшиеся конденсации быстро собирают большую часть «неиспользованной массы» и затем начинают сжиматься, образуя протозвезды, протогалактики и т.д.
Отметим еще одно обстоятельство. В формуле Джинса нет какой-либо фундаментальной длины, определяемой атомными или какими-либо другими константами. Поэтому, если имеется непрерывный ряд изменения начальных параметров среды — плотности и температуры-мы получим сплошной спектр длин волн неустойчивости. Не исключено, что непрерывный ряд характерных размеров небесных тел — звездных скоплений, галактик, скоплений галактик — есть свидетельство того, что в прошлом во Вселенной имел место процесс гравитационной конденсации.
Обсудим теперь, после выяснения общего физического смысла механизма гравитационной неустойчивости, некоторые дополнительные соображения. Рассмотрим плоскую систему, например, вращающуюся галактику. В этом случае вместо объемной плотности мы должны ввести поверхностную плотность массы
 |
В этом случае критерий Джинса приобретает вид
 | (8.19) |
Эта формула получена Леду [11]. Здесь λ — толщина гравитационно-устойчивого слоя или диска. Этой формулой можно объяснить известный из радионаблюдений факт утолщения газового диска Галактики от центра к периферии. Толщина диска связана с плотностью, и по мере убывания плотности к периферии толщина диска растет.
Далее, если образующиеся сгущения вращаются, например из-за несимметричности в начальный момент, то при сжатии угловая скорость увеличивается в соответствии с теоремой сохранения углового момента. Тогда условие, требующее, чтобы сгущение не разлетелось из-за вращения, имеет вид
 | (8.20) |
где ΔΩ;;; — изменение угловой скорости в пределах рассматриваемого сгущения.
Вопрос о вращении конденсаций (протогалактик) можно рассмотреть с другой стороны. Пусть мы имеем выделившуюся в результате джинсовской неустойчивости конденсацию с вращением. Она характеризуется следующими параметрами: массой, вращательным моментом, постоянной тяготения (конденсация гравитационно связана), и температурой, которую будем выражать через скорость звука. Найдем зависимость между этими факторами. Матрица размерности
 |
дает единственный безразмерный комплекс, откуда следует формула
 | (8.21) |
Постоянная согласно [12] равна 12/5 π . Аналогичная формула для релятивистского диска 



Итак, если галактика «помнит» начальные условия своего образования и зависимость 

Обсудим теперь эффекты магнитного поля. Магнитное поле, как и упомянутое ранее вращение, фактор существенно анизотропный. Магнитное поле препятствует сжатию в направлении, перпендикулярном к силовым линиям. Вдоль этих линий поле не только не препятствует сжатию, но и способствует ему (неустойчивость Пикельнера — Паркера).
Для количественных оценок можно считать характерной скоростью скорость альвеновских волн
 | (8.22) |
или сравнивать гравитационное и магнитное давления
 | (8.23) |
На ранних стадиях эволюции Вселенной магнитное давление может превосходить давление газа, и в этих условиях влияние магнитного поля на процесс образования галактик может оказаться существенным. Хотя наблюдательные данные по далеким радиогалактикам еще не дают однозначных выводов о наличии и величине поля, его существование в принципе не исключено. В частности, магнитное поле могло бы объяснить любопытный факт выстраивания галактик цепочками. В этом случае естественно предполагать гравитационную неустойчивость некоторой цилиндрической конфигурации, образовавшейся под действием магнитного поля. Гравитационная неустойчивость космологических моделей с первичным магнитным полем, приводящая к образованию дисковых (двумерных) и нитевидных (одномерных) образований, рассматривалась в работе [15].
Итак, в общем случае для сгущения, выделившегося из первично однородной среды благодаря механизму гравитационной неустойчивости, можно записать условие равновесия
 | (8.24) |
где vR — вращательная скорость, 〈 v〉 — турбулентная скорость. В такой формулировке условие равновесия (8.24), как можно видеть, эквивалентно известной теореме вириала.
Источник
Гравитационная неустойчивость во вселенной
ГРАВИТАЦИОННАЯ НЕУСТОЙЧИВОСТЬ — нарастание возмущений (малых отклонений от ср. значения) плотности и скорости вещества под действием сил тяготения. При первоначально близком к однородному распределении вещества в космич. пространстве Г. н. должна приводить к образованию сгустков. Г. н. рассматривается как причина образования галактик и их скоплений, а также звёзд и звёздных скоплений (см. Звездообразование ). Идея Г. н. была высказана И. Ньютоном в 1692 г. Однако математич. разработка теории Г. н. началась лишь после работы англ. физика Дж. Джинса (1902 г.), рассматривавшего вопросы происхождения звёзд и др. космич. объектов. К 80-м гг. 20 в. теория Г. н. разработана для однородной среды (в связи с теорией происхождения галактик и скоплений галактик), а также для простейших геометрич. конфигураций: плоского слоя; осесимметричных конфигураций, неоднородных по радиусу; тонкого диска. Развитие возмущений в таких простейших конфигурациях исследуется с целью объяснения происхождения наблюдаемой внутр. структуры галактик.
Однородное (или близкое к однородному) распределение вещества при наличии сил тяготения явл. неустойчивым относительно распада на отдельные сгустки большей плотности, т. к. этот процесс сопровождается уменьшением потенциальной энергии. Гравитационная энергия при сжатии переходит в кинетич. энергию сжимающегося вещества, к-рая может в дальнейшем переходить в теплоту и излучаться.
Силам тяготения противодействуют упругость вещества (определяемая градиентом давления) и, возможно, др. негравитац. силы (эл.-магн., центробежные, вызванные вращением сгустка, и др.). Соотношение между силами тяготения и противодействующими силами зависит от размеров возникающего сгустка. Для однородной среды силы тяготения пропорциональны размеру сгустка l, тогда как, напр., сила упругости, связанная с градиентом давления, пропорциональна 1/l (градиент давления тем больше, чем на более малом расстоянии происходит изменение давления на данную величину). Поэтому при больших l силы тяготения велики по сравнению с силами упругости, и сгусток больших размеров сжимается. Напротив, при малых l силы тяготения малы по сравнению с силами упругости. Силы упругости приводят к расширению сгустка повышенной плотности — возникают колебания, распространяющиеся со скоростью звука по окружающему веществу. Т. о., среда устойчива относительно распада на отдельные мелкомасштабные сгустки и неустойчива относительно образования сгустков больших размеров.
Если рассматривать лишь силы тяготения и упругости, то критич. значение l, отделяющее область устойчивости от области Г. н., соответствует т. н. длине волны Джинса
где aзв — скорость звука, r — плотность вещества.
Аналогичные ф-лы для критич. размера lдж могут быть получены и при учёте вращения, турбулентности, эл.-магн. и иных сил, противодействующих силам тяготения. Наличие этих сил повышает устойчивость вещества в нек-рых направлениях и увеличивает критич. размер, соответствующий длине волны Джинса. Однако вдоль магн. поля или вдоль оси вращения размер ее меняется. На основе анализа устойчивости упомянутых выше простейших конфигураций с неоднородным распределением газа можно сделать вывод о существовании и в этих случаях критич. размера, отделяющего область устойчивости от области неустойчивости относительно малых возмущений. Зависимость критич. размера от локальной плотности и скорости звука подобна приведённой выше.
Скорость роста возмущений, вызванных силами тяготения, зависит от характерного размера возмущений. Возмущения в масштабах меньше критич. lдж не нарастают вовсе. Возмущения в масштабах больше критического растут тем быстрее, чем больше масштаб. В пределе (для очень крупных по размеру возмущений l >> lдж) скорость роста возмущений перестаёт зависеть от их масштаба, и возмущения нарастают с сохранением начальной формы (в т. н. автомодельном режиме). Здесь упругость газа уже не играет роли и происходит как бы свободное падение к центру конденсации. При этом зависимость возмущений плотности и скорости от координат не изменяется — в каждой точке возмущения растут с течением времени по одному и тому же закону. Всё это относится к начальному развитию возмущений, пока они относительно малы. С ростом возмущений закон изменяется, и, как правило, сжатие останавливается.
Возмущения больших масштабов (l >> lдж) на фоне стационарного среднего распределения вещества нарастают со временем экспоненциально, пропорционально e w t . Величина w , определяющая скорость возрастания возмущений, зависит от характерной плотности среды r . По порядку величины 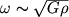
По иному закону происходит нарастание возмущений на фоне расширяющегося или сжимающегося вещества. В результате расширения изменяются плотность вещества и скорость звука в нём, что в свою очередь приводит к изменению lдж и w . Этот случай рассматривается в рамках однородной и изотропной космологич. модели Фридмана (модели расширяющейся Вселенной, см. Космология ). В рамках модели Фридмана сделаны успешные попытки объяснить возникновение наблюдаемых неоднородностей — галактик и скоплений галактик — действием Г. н.
Изотропное расширение (или сжатие) однородного вещества происходит по Хаббла закону : u = Нr, где u — относительная скорость движения двух произвольных точек среды, находящихся на расстоянии r друг от друга, Н — постоянная Хаббла. Для полного анализа Г. н. такой среды необходимо использовать общую теорию относительности (ОТО). Однако осн. закономерности могут быть получены и в рамках теории тяготения Ньютона.
Однородная изотропно расширяющаяся среда устойчива относительно малых возмущений при плотности много меньшей т. н. критич. плотности r с = 3H 2 /8 p G » 2 . 10 -29 г/см 3 , ибо в этом случае тяготение не может остановить расширение вещества (независимо от газового давления). Если это условие не выполнено, относительные возмущения плотности и скорости отстают от общего расширения и нарастают (при условии l >> lдж). Следует подчеркнуть, что однородная изотропно сжимающаяся среда всегда неустойчива.
В расширяющейся (сжимающейся) среде возмущения нарастают не экспоненциально, как в стационарной среде, а по степенному закону, пропорционально t a , где t — время, отсчитанное от момента, когда плотность вещества в модели Фридмана бесконечна. Показатель степени a различен для расширяющейся и сжимающейся сред и зависит от ур-ния состояния вещества. Напр., если скорость звука мала по сравнению со скоростью света, азв r » r с, то относительные возмущения плотности при расширении нарастают по закону Dr / r
t 2/3 (l >> lдж), а при сжатии (t Dr / r
Согласно модели горячей Вселенной , плотность излучения в далёком прошлом превосходила плотность вещества, и динамика расширения определялась излучением. В этих условиях скорость звука близка к скорости света с(
Приведённые ф-лы показывают, что существовавшие на начальных стадиях расширения неоднородности растут со временем. В фридмановской модели при достижении значения Dr / r » 1 наступает нелинейная стадия роста неоднородностей и возможно образование галактик и скоплений галактик.
Лит.: Новиков И. Д., Эволюция Вселенной, 2 изд., М., 1983; Зельдович Я. Б., Новиков И. Д., Релятивистская астрофизика, М., 1967; их же, Теория тяготения и эволюция звезд, М., 1971; их же, Строение и эволюция Вселенной, М., 1975; Поляченко В. Л., Фридман А. М., Равновесие и устойчивость гравитирующих систем, М., 1976; Шандарин С. Ф., Дорошкевич А. Г., Зельдович Я. Б., Крупномасштабная структура Вселенной, «УФН», 1983, т. 139, в. 1.
Источник