На каком расстоянии Луна от Земли и как было измерено это расстояние?
Минимальное и максимальное расстояние между Землей и Луной, способы измерения расстояния до Луны и диаметра спутника нашей планеты
Как измеряли расстояние до планет в древности?
Представьте себя на месте человека не знакомого со строением Солнечной системы, наблюдающего за ночным небосводом. Звезды, сами по себе, вам представляются неподвижными объектами, но вот само звездное небо вроде как вращается, причем вращается вокруг Земли и совершает полный оборот за 24 часа.
Легко сделать вывод, располагая таким данными, что звезды “прикреплены” к небесному своду, представляющему собой своеобразное “покрывало”, окутывающее нашу планету со всех сторон. Это наблюдение очевидное и простое и потому, вплоть до самого XVII века – главенствующее и даже “научное”.
В то же время, уже в древности люди замечали, что некоторые небесные светила движутся среди звезд — а следовательно, эти светила не могли быть прикреплены к небесному своду и находились к Земле ближе, чем само небо. Насчитывалось семь таких небесных тел, называвшихся (в порядке их яркости) Солнце, Луна, Венера, Юпитер, Марс, Сатурн и Меркурий. Эти семь небесных тел греки называли «планетес» (скитальцы или “блуждающие звезды”), так мы до сих пор большинство из них и называем – «планеты».
Пропорции Земли и Луны – да, наш спутник не так уж и мал, всего в 4 раза уступая Земле по размеру. Впрочем, при этом он легче в 80 раз.
Дальнейшие наблюдения показали – можно установить, какие из планет находятся ближе к Земле, а какие — дальше от нее. Например, при каждом солнечном затмении Луна проходила между Землей и Солнцем и, следовательно, Луна была ближе к Земле, чем Солнце.
При оценке других расстояний древние исходили из относительной скорости движения планет среди звезд (чем ближе к нам предмет, тем более быстрым кажется его движение). Исходя из относительной скорости движения планет среди звезд, греки решили, что Луна расположена ближе к Земле, чем остальные планеты. Прочие же располагались в порядке увеличения расстояния так: Меркурий, Венера, Солнце, Марс, Юпитер и Сатурн.
Разумеется, в таком случае при определении расстояний от планет до Земли следовало начинать с ближайшего светила – то есть Луны.
Как Гиппарх измерил расстояние до Луны?
Первую серьезную попытку определить расстояние до Луны предпринял греческий астроном Аристарх Самосский (320—250 гг. до н. э.). Он опирался на наблюдения, сделанные во время лунного затмения. Когда тень Земли упала на Луну, по изгибу ее края можно было судить, как велико ее поперечное сечение по сравнению с размерами Луны.
Кажется, что Луна совсем близко от Земли. Вот так выглядит расстояние между Землей и Луной в натуральных пропорциях. 384 000 километров – не так и близко, а?
Считая, что Солнце находится от Земли гораздо дальше Луны, Аристарх с помощью несложных геометрических построении мог установить, как далеко должна Луна находиться от Земли, чтобы тень Земли уменьшалась до наблюдаемых размеров.
Этот метод был улучшен и дополнен примерно через 100 лет другим греческим астрономом — величайшим астрономом античности Гиппархом из Никеи (190— 120 гг. до н. э.). Гиппарх пришел к выводу, что расстояние от Земли до Луны примерно в 30 раз больше диаметра Земли. Если принять длину диаметра, предложенную Эратосфеном, т.е. 12 800 км, то в этом случае расстояние между Землей и Луной окажется равным 384 000 км.
Это блистательный результат, если учесть тогдашнее состояние астрономии. Наиболее точная современная цифра среднего расстояния между центрами Земли и Луны — 384 395 км. Не располагая и сотой долей тех возможностей, которыми располагает астрономия сейчас, Гиппарх из Никеи провел вычисления с погрешностью в 1/1000!
Как был измерен диаметр Луны
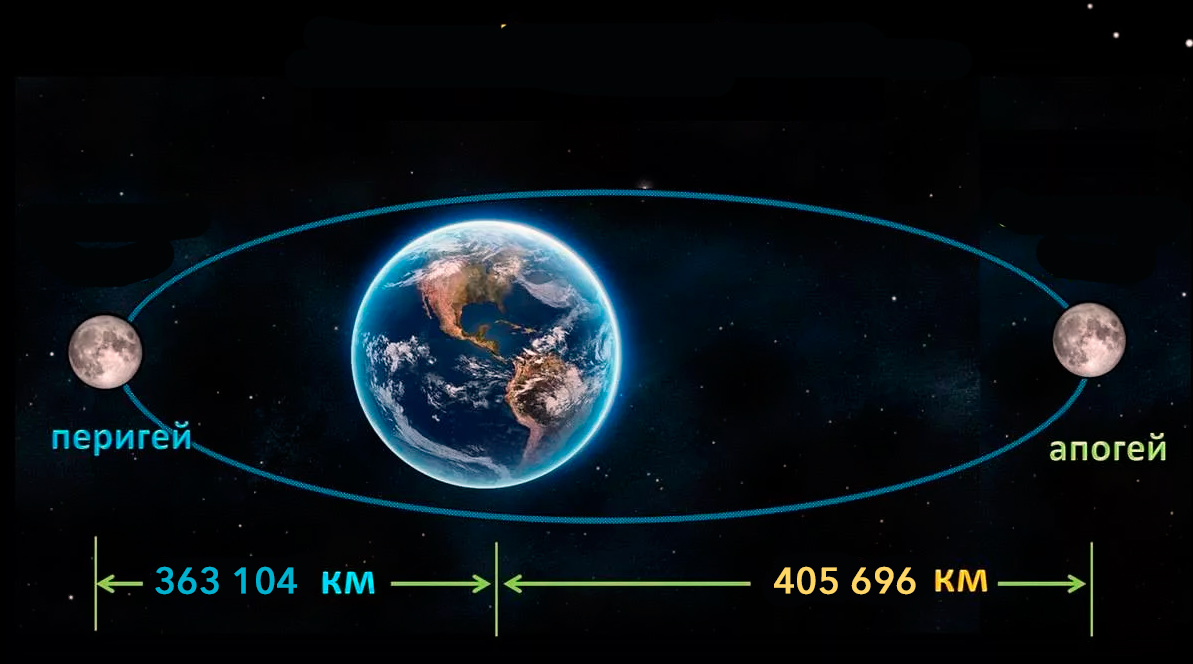
Конечно же, 384 395 километров – среднее расстояние между Землей и Луной, так как Луна движется вокруг Земли не по точному кругу: иногда она ближе к нашей планете, а иногда дальше.
Минимальное расстояние между Луной и Землей (в перигее) равно 363 300 км, а максимальное (в апогее) —405 500 км.
Зная это расстояние, можно вычислить истинный диаметр Луны, исходя из ее видимых размеров. Он равен 3473,4 км, а окружность Луны, следовательно, составляет 10 900 км. Луна намного меньше Земли, но все же ее размеры весьма внушительны.
После того как было определено расстояние до Луны, с идеей о том, что небо находится почти над самыми нашими головами, было покончено навсегда. Оно отодвинулось на колоссальное расстояние, представлявшееся грекам немыслимым.
Даже ближайшее небесное тело оказалось почти в 400 000 км от Земли, а все другие, значит, находились от нее еще дальше и, возможно, намного дальше. Ни о какой “плоской Земле накрытой стеклянным куполом” больше не могли помыслить даже самые стойкие скептики.
Перигей и апогей Луны по отношению к Земле – самое близкое и самое дальнее расстояние между Луной и Землей
Источник
Как измерили расстояние от Земли до Луны?
Расстояние от Земли до Луны пытались измерить еще древние греки.
До нас дошло только сочинение Аристарха Самосского «О величинах и расстояниях Солнца и Луны» (III в. до н. э.), где он впервые в истории науки попытался установить расстояния до этих небесных тел и их размеры.
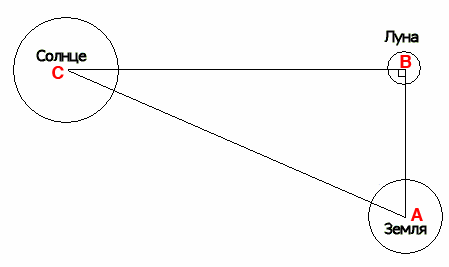
К решению этого вопроса Аристарх подошел очень остроумно. Он исходил из предположения, что Луна имеет форму шара и светит отраженным от Солнца светом. В этом случае, в те моменты, когда Луна имеет вид полудиска, она образует прямоугольный треугольник с Землей и Солнцем:
Если в этот момент точно определить угол между направлениями с Земли на Луну и на Солнце (CAB), можно из простых геометрических соотношений найти, во сколько раз катет (расстояние от Земли до Луны AB) меньше гипотенузы (расстояния от Земли до Солнца AC). По Аристарху, CAB=87°; следовательно, соотношение этих сторон 1:19.
Аристарх ошибся приблизительно в 20 раз: в действительности расстояние до Луны меньше, чем до Солнца, почти в 400 раз. Загвоздка заключается в том, что точно определить момент, когда Луна оказывается в вершине прямого угла, лишь на основе наблюдений невозможно. Малейшая же неточность влечет за собой огромное отклонение от истинного значения.
Величайший астроном древности Гиппарх Никейский в середине II века до н. э. с большой уверенностью определил расстояние до Луны и ее размеры, приняв за единицу радиус земного шара.
В своих вычислениях Гиппарх исходил из правильного понимания причины лунных затмений: Луна попадает в земную тень, имеющую форму конуса с вершиной, находящейся где-то в стороне Луны.
Посмотрите на рисунок. Он показывает положение Солнца, Земли и Луны во время лунного затмения. Из подобия треугольников следует, что расстояние от Земли до Солнца AB во столько раз больше расстояния от Земли до Луны BC, во сколько раз разность радиусов Солнца и Земли (AE — BF) больше разности радиусов Земли и ее тени на расстоянии Луны (BF — CG).
Из наблюдений при помощи простейших угломерных инструментов следовало, что радиус Луны составляет 15′, а радиус тени приблизительно 40′, то есть радиус тени больше радиуса Луны почти в 2,7 раза. Приняв расстояние от Земли до Солнца за единицу, можно было установить, что радиус Луны почти в 3,5 раза меньше радиуса Земли.
Уже было известно, что под углом в 1′ наблюдается предмет, расстояние до которого превосходит его размеры в 3 483 раза. Следовательно, рассуждал Гиппарх, под углом в 15′ наблюдаемый предмет будет в 15 раз ближе. Значит, Луна находится от нас на расстоянии, в 230 раз (3 483 : 15) превосходящем ее радиус. А если радиус Земли составляет приблизительно 3,5 радиуса Луны, то расстояние до Луны равно 230 : 3,5
60 радиусов Земли, или около 30 земных диаметров (это около 382 тыс. километров).
В наше время измерение расстояния от земли до Луны было выполнено с помощью метода лазерной локации. Суть этого метода заключается в следующем. На поверхности Луны устанавливается уголковый отражатель. С Земли с помощью лазера на зеркало отражателя направляется лазерный луч. При этом точно фиксируется время, когда сигнал был излучён. Отражённый от прибора на Луне свет в течение примерно одной секунды возвращается в телескоп. Определив точное время, за которое луч света проходит расстояние от Земли до Луны и обратно, можно установить расстояние от источника излучения до отражателя.
С помощью этого метода расстояние от земли до Луны определено с точностью до нескольких километров (максимальная точность измерения в настоящее время — 2-3 сантиметра!): в среднем оно составляет 384 403 км. «В среднем» не потому, что это расстояние взято из разных или приблизительных результатов измерений, а потому, что орбита Луны представляет собой не окружность, а эллипс. В апогее (наиболее удаленная от Земли точка орбиты) расстояние от центра Земли до Луны 406 670 км, в перигее (наиболее близкая точка орбиты) — 356 400 км.
Источник
Как далеко до Луны?
Как без помощи Google, Википедии и NASA узнать расстояние от Земли до Луны
Представьте, что вы смотрите на луну зимним вечером и задаетесь вопросом: «Как далеко находится Луна?». Что бы вы сделали, чтобы рассчитать, насколько это далеко? Самое простое решение — заглянуть в Google. Но, как же тогда греки, которые задавали тот же вопрос 2200 лет назад, и нашли ответ на него без помощи Google, Википедии и NASA или любой современной технологии? Греки смогли определить достаточно точное расстояние от Земли до Луны, используя тщательные наблюдения, измерения и изящную геометрическую модель.
Определение ключевой информации
Греческий астроном и математик, Аристарх Самосский, вычислил расстояние от Земли до Луны только пользуясь следующей информацией:
- Диаметр Земли равняется приблизительно 8 000 миль или 12 800 км (еще один гениальный расчет, сделанный Эратосфеном).
- Тени, отбрасываемые небесными телами, имеют коническую форму и считаются похожими. В двумерном виде тени, отбрасываемые Луной и Землей, являются подобными равнобедренными треугольниками:
Следующая информация была получена в результате пристального наблюдения лунных затмений.
- Во время полного лунного затмения наблюдалось, что Луна проходила через земную тень расстояние, равное диаметру двух с половиной своих дисков.
Формулирование модели
На основе этой информации была разработана модель. В этой модели тень от Луны разворачивается зеркально по отношению к земной тени, а сама Луна располагается так, что одна сторона её тени выравнивается с одной стороной земной тени. При этом конец лунной тени сужается достигая Земли.
Пусть диаметр Луны равен 1 единице. Тогда AF составляет 1 единицу, а FD должен составлять 2,5 единицы, что согласуется с наблюдениями за лунными затмениями.
Как указывалось выше, треугольники теней — ABF и BEC подобны. Следовательно углы BEC и ABF равны. Из этого следует, что линии AB и EC взаимно параллельны. Также параллельны линии AD и BC. Поэтому прямоугольник ABCD является прямоугольником, в котором противоположные стороны равны. А, следовательно, BC = AD.
ВС — это диаметр Земли, который, как известно из исходных данных, составляет примерно 8 000 миль или 12 800 км.
AD — это 3,5 диаметра Луны. Из равенства ВС=AD можно рассчитать этот диаметр, который будет равен примерно 2 285 миль (8000/3,5) или около 3 500 км.
Основываясь на информации, с которой мы начали, расстояние между Землей и Луной составляет 108 диаметров Луны или примерно 378 000 км (3500 x 108).
Современные расчеты показывают, что расстояние от Земли до Луны из-за эллиптической орбиты спутника колеблется от 363 тыс.км (перигей) до 406 тыс.км (апогей), а большая полуось орбиты составляет 384 тыс.км. Невероятно, но Аристарху удалось сделать достаточно точную оценку этого расстояния, учитывая инструменты, которые он имел в своем распоряжении, и астрономические масштабы, с которыми он работал.
Источник
Как измерили расстояние от Земли до Луны?
Когда я читал произведение Жюля Верна «Из пушки на Луну», для меня стало открытием, что еще в XIX веке люди знали, сколько км до Луны. Мало того, они еще и умудрялись вычислять высоту лунных гор!
Копнув поглубже, я узнал, что расстояние от нашей планеты до ее спутника довольно точно вычислили еще древние греки. Ладно европейцы лет 200 назад – у них были телескопы, инструменты там всякие… Но греки-то как?
Фазы Луны
Вообще, древние были людьми наблюдательными и сообразительными. Они сразу поняли, что Луна не светит сама по себе, она лишь отражает свет Солнца, да и висит намного ближе к нам.
Они правильно объяснили фазы Луны. Представьте, что Вы – это и есть планета Земля и смотрите лицом вперед прямо на Солнце. Если Луна за вашей спиной, то наступает полнолуние, а если перед вами – то новолуние, когда он исчезает полностью (её затмевает солнечный свет). Все промежуточные состояния, когда Луна походит на кусок сыра происходят из-за того, что Луна либо справа, либо слева от Вас и освещается только наполовину.
Древнегреческий астроном Аристарх догадался, что в определенный момент, когда освещена ровно половина обращенной к нам стороны Луны, она вместе с Землей находится на одинаковом расстоянии от Солнца. Все равно что солдаты, выровнявшиеся на одной линии перед своим командиром.
Получается, что эти три объекта лежат в треугольнике, где Луна – это прямой угол. «Стоп, пусть я не могу узнать размеры этого треугольника, зато могу вычислить его углы!» — воскликнул Аристарх.
Аристарх берется за работу
Ранним утром, когда Луна была над горизонтом, он нарисовал на земле треугольник. Одна его вершина указывала на дневное светило, другая – на ночное. В третьей точке стоял он сам. Когда он завершил свой чертеж, то смог измерить каждый угол и вычислить соотношение сторон (помните – синусы, косинусы…), а значит и расстояний от Земли до Солнца и до Луны. Получалось, что последняя ближе к нам в 400 раз.
Аристарх жил долго и смог застать при своей жизни солнечное затмение. Луна закрыла собой Солнце, но лишь на несколько мгновений. Почему? «Да просто они на небе одинакового размера», — подумал он. Получается, что Луна и ближе в 400 раз, и меньше Солнца в 400 раз!
Ладно, допустим, что соотношение он вычислил, но ведь этого мало. Если увеличить все размеры и расстояния, то соотношение все равно бы сохранялось, и мы бы не заметили, что Луна стала дальше от нас. Как быть?
Надо было как-то соотнести все это с размером самой Земли, которое до этого вычислил его соотечественник Эратосфен. Для этого подходило лунное затмение, когда земная тень закрывал собой Луну. Аристарх выяснил, что земная тень больше Луны приблизительно в 2,66 раз. Исписав не один листок пергамента, он все-таки вычислил, что настоящий радиус Земли больше радиуса Луны в 3,66 раз.
В обычном треугольнике, чтобы узнать все его размеры, достаточно вычислить два угла и одну сторону. Аристарх провел от Земли две линии к Луне. Одна упиралась в его центр, другая касалась самой поверхности. Перед вами готовый прямоугольный треугольник, где вы знаете одну сторону – радиус Луны и один угол – он прямой, то есть 90 градусов.
Оставалось найти еще один. Пришлось найти угол, под которым видно половину Луны – это около полградуса. Всё, все данные собраны, можно приступать к вычислениям. У греков получилась цифра, почти близкая к нынешней.
Зная расстояние до Луны и ее размеры, древние смогли вычислить, насколько огромно наше Солнце и как же оно от нас далеко.
На самом деле сам Аристарх не смог вычислить все правильно, у него цифры получились гораздо меньше. Многие думают, что он просто испугался столь больших чисел и не поверил увиденному. Но важно, что он разработал саму методику, который воспользовался Гиппарх, который через сто лет после него смог найти правильные значения для размеров и расстояний до небесных тел.
Вот и всё. Оказывается, что измерить Луну и узнать, сколько до нее, можно и без телескопа.
Источник