Звездные координаты и экваториальные системы
Как известно, люди с древних времён использовали звездные координаты в своей повседневной жизни. Например, по светилам мореплаватели ориентировались в пространстве, да и не только они, начинались или заканчивались сельскохозяйственные работы и многое другое. Более того, создавались настоящие календари работ, где положение звезд, можно сказать, советовало и диктовало людям когда и чем заниматься.
Какие существуют звездные координаты и системы
Разумеется, с течением времени человек более или менее упорядочил информацию о светилах. В результате в астрономии существует несколько видов систематизации звёзд.
Горизонтальная или топоцентрическая система
Проще говоря, она отражает положение светил относительно земного горизонта. Если точнее, то показывает две звездные координаты:
1) Высота над горизонтом, имеющая угловое значение и измеряемая в градусах. Здесь важно понимать, что обозначает расположение объекта.
Во-первых, наивысшая точка — зенит (+90). Во-вторых, если звёздное тело лежит на линии горизонта, то значит имеет нулевое значение. И, в-третьих, прямо противоположное зениту положение-надир (-90), когда светило находится как будто прямо под наблюдателем.
2) Азимут — угловое значение между линиями, лежащими на горизонте, которые имеют направление на объект и на север.
Горизонтальную систему часто называют топоцентрической, поскольку данные звездные координаты связаны с какой-либо определённой точкой на земной поверхности.
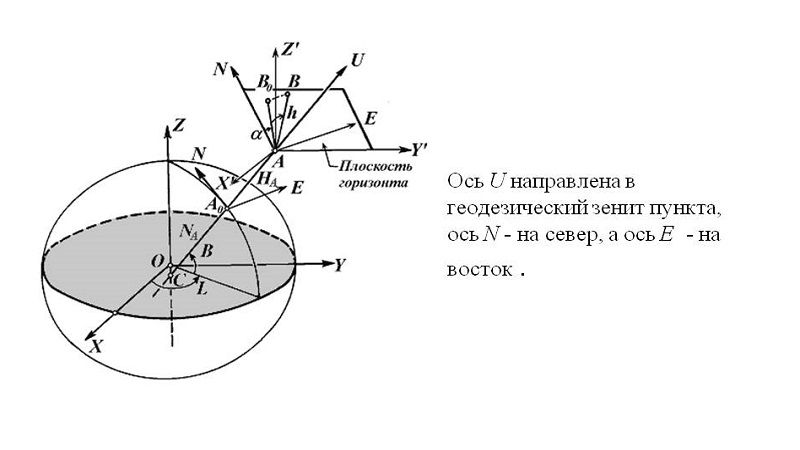
Стоит отметить, что оба значения постоянно меняются, поэтому определять координаты звезд на звездной карте довольно проблематично.
Первая экваториальная система
В отличие от предыдущей, экваториальные координаты звезд связаны не только с земной поверхностью, но и со сферой неба. Более того, основной плоскостью выступает небесный экватор. Также имеет две основные звездные координаты:
1) Склонение, которое, к слову, относительно постоянно. Для его определения измеряют угол между экваториальной плоскостью и прямой линией, направленной на звезду.
Как оказалось, дуга круга склонения отсчитывается к северному полюсу мира от 0 до +90 градусов, а также к южному полюсу мира от 0 до -90 градусов.
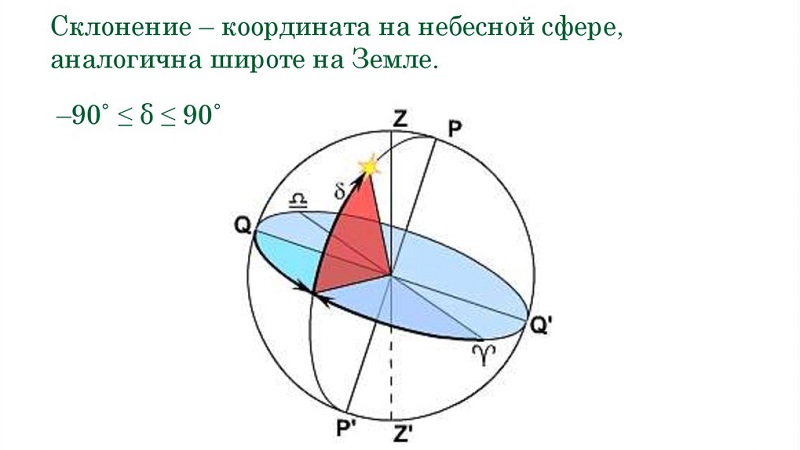
2) Часовой угол между небесным меридианом и линией, направленной на светило. Прежде всего, эта координата зависит от того, где и в какое время располагается наблюдатель.
А вот отсчёт часового угла ведётся в сторону суточного вращения неба от 0 до 360 градусов (в сторону запада).
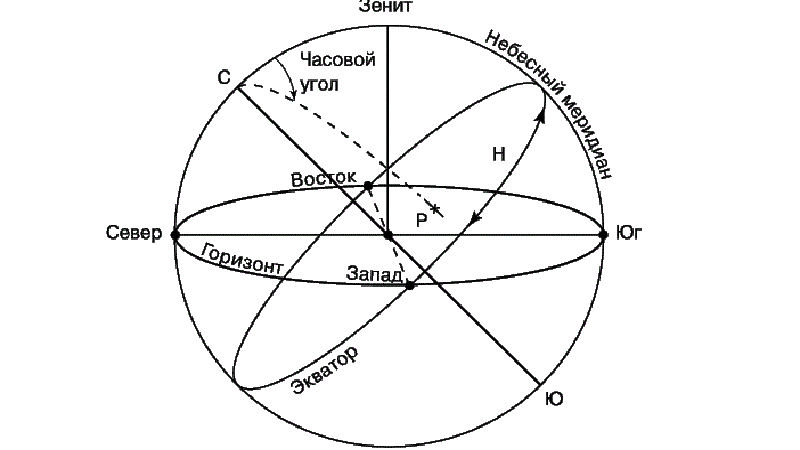
Небесный меридиан — круг небесной сферы, проходящий сквозь зенит, полюс мира, южный полюс и надир.
Однако применение данной системы не совсем удобно для того, чтобы определять положение звезд.
Вторая экваториальная система
Вот её как раз применяют для определения звездных координат на небесной сфере. Хотя основной плоскостью также является экваториальная плоскость неба. Правда, одна из её координат точно такая же, как у первой системы. А именно склонение.
Собственно говоря, отличие заключается во втором значении положения светила. Она называется прямым восхождением и отражает угол между двумя линиями, расположенными на небесном экваторе, которые пересекаются там, где этот экватор пересекается с осью мира.
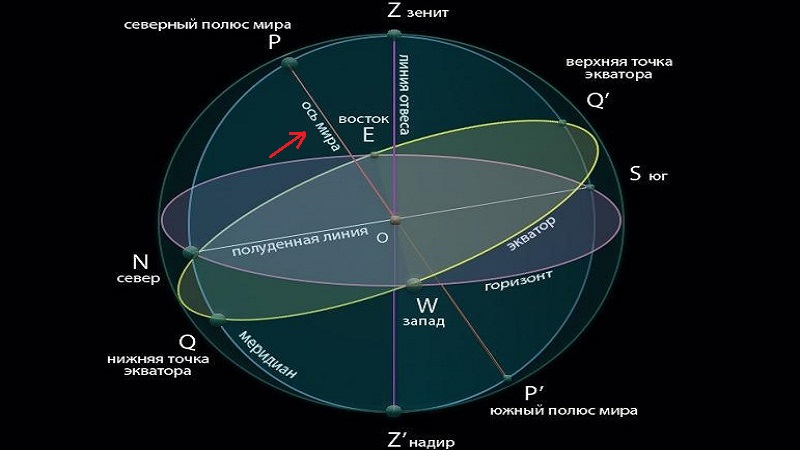
Таким образом получается, что первая линия тянется к точке весеннего равноденствия, а вторая к точке проекции звезды на экватор неба.
Прямое восхождение, точнее его угол, измеряется по экваториальной дуге. Причем обязательно по часовой стрелке. Что интересно, единицей измерения могут быть как градусы, так и минуты и часы. Один час равен 15 градусам.
Между прочим, во второй системе оси являются недвижимыми для удалённых объектов космоса.
Ось мира — это прямая, соответствующая географической земной оси, которая проходит сквозь небесный свод в Северном и Южном полюсах мира.
Эклиптическая система
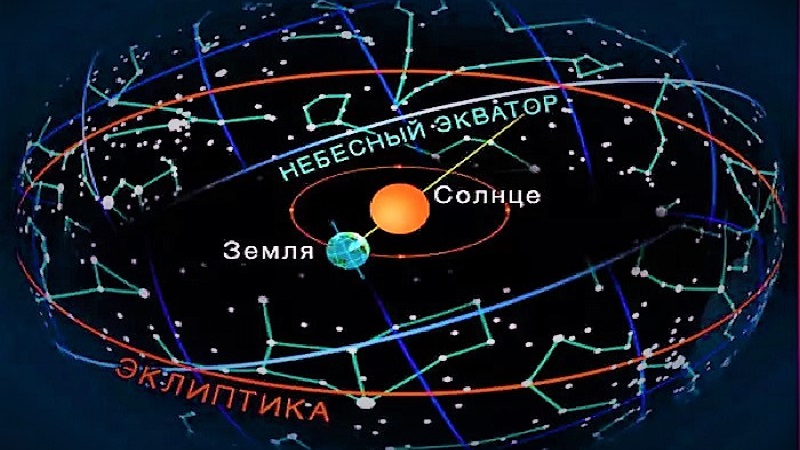
Для того, чтобы определять координаты близких к Земле звезд на звездной карте неба, используют эклиптическую систему. Главным образом, она отличается от других способов тем, что за основную плоскость берут плоскость эклиптики. То есть область, где проходит земная орбита при вращении вокруг Солнца.
Звездные координаты эклиптической системы:
- Широта эклиптики-дуга круга широты, которая берёт начало от эклиптики и протянута до светила.
- Долгота эклиптики-дуга от точки весеннего равноденствия до круга широты звёзд.
Помимо того, что такой подход позволяет узнать положение ближайших космических тел, его использование показывает, где находится Земля относительно других астрономических объектов.
Галактическая система
На самом деле, галактическая система координирования необходима при более масштабных поисках и расчётах. Поскольку ни один из перечисленных выше способов не актуален при определении расположения удалённых от нас космических объектов, к примеру галактик и туманностей.
Здесь, собственно говоря, основой выступает плоскость галактики Млечный Путь. А координирующими значениями являются галактические широта и долгота.

Таблица экваториальные координаты звезд
Как вы понимаете, здесь важно отметить значения склонения и прямого восхождения светил. Например, возьмём несколько разных звёзд.
| Звезда | Склонение (градусы/минуты) | Прямое восхождение (ч/мин) |
| Альтаир | +8/44 | 19/48,3 |
| Арктур | +19/27 | 14/13,4 |
| Вега | +38/44 | 18/35,2 |
| Ригель | -8/15 | 5/12,1 |
координаты некоторых звезд
Итак, для того, чтобы найти звезды, используют поиск по координатам. Ведь они как раз отражают местоположение тела на карте неба. Кроме того, для определения их положения также применяют координаты или определённую систему.
Как видно, звездные координаты указывают с помощью двух величин или дуг, которые характеризуют, где располагается звезда на небесной сфере. Помимо этого, можно выделить главные различия между каждой системой. В первую очередь, это выбор центральной плоскости. А во вторую очередь, отличие заключается в выборе начала отсчёта.
Стоит отметить, что карта неба не отражает расстояние до светил. А лишь указывает, где они находятся. Вероятно, по этой причине при ориентировании на местности удобно обращаться к светящимся космическим соседям. Что, собственно говоря, на протяжении многих лет и делали люди.
Источник
Практическое определение географических и небесных экваториальных координат
В долгие зимние ночи астрономы измеряют зенитные расстояния одних и тех же звезд в обеих кульминациях и по формулам (4), (6), (9) независимо находят их склонение (δ) и географическую широту (φ) обсерватории. Зная φ, определяют склонение светил, у которых наблюдается только верхняя кульминация. При высокоточных измерениях учитывается рефракция, которая здесь не рассматривается, кроме случаев расположения светил вблизи горизонта.
В истинный полдень регулярно измеряют зенитное расстояние z 

sin α 

где ε = 23°27′ — уже известное наклонение эклиптики.
Одновременно определяется и поправка звездных часов
us = S—Sч = α 
так как в истинный полдень часовой угол Солнца t 

Отмечая показания S’ч тех же часов в моменты верхней кульминации ярких звезд (они видны в телескопы и днем), находят их прямое восхождение
α=α 
и по нему аналогичным образом определяют прямое восхождение остальных светил, которое также может быть найдено как
По публикуемым в астрономических справочниках экваториальным координатам (α и δ) звезд определяют географические координаты мест земной поверхности.
Пример 1.В истинный полдень 22 мая 1975 г. зенитное расстояние Солнца в Пулкове было 39°33′ S (над точкой юга), а звездные часы показывали 3ч57м41с. Вычислить для этого момента экваториальные координаты Солнца и поправку звездных часов. Географическая широта Пулкова φ = +59°46′.
Данные: z 
Решение. Согласно формуле (4), склонение Солнца
δ 

sinα 

откуда прямое восхождение Солнца α 

Так как в истинный полдень, согласно формуле (13), звездное время S = α 
us=S—Sч=α 
Пример 2.В момент верхней кульминации звезды α Дракона на зенитном расстоянии 9°17′ к северу звездные часы показывали 7ч20м38с, причем их поправка к звездному гринвичскому времени равнялась +22м16с. Экваториальные координаты α Дракона: прямое восхождение 14ч03м02с и склонение + 64°37′. Определить географические координаты места наблюдения.
Данные: звезда, α = 14ч03м02с, δ=+64°37′, zв = 9°17′ N; звездные часы Sч = 7ч20м38с, us = 22м16с.
Решение. По формуле (6), географическая широта
φ = δ—zв = + 64°37’—9° 17’= + 55°20′.
Согласно формуле (13), звездное время в месте наблюдения
S =α=14ч03м02c, а звездное время в Гринвиче S0 = Sч+us=7ч20м38c+22м16c = 7ч42м54c.
Следовательно, по формуле (14), географическая долгота
λ = S—S0 = 14ч03м02с—7ч42м54с = 6ч20м08с,
или, переведя в угловые единицы, λ=95°02′.
Задача 70.Определить географическую широту места наблюдения и склонение звезды по измерениям ее зенитного расстояния z или высоты h в обеих кульминациях—верхней (в) и нижней (н):
а) zв=15°06’W, zн = 68°14′ N;
б) zв=15°06′ S, zн=68°14′ N;
в) hв=+80°40′ ю, zн=72°24′ c;
г) hв=+78°08’ю, hн= + 17°40′ ю.
Задача 71.В местности с географической широтой φ = = +49°34′ звезда α Гидры проходит верхнюю кульминацию на высоте +32°00′ над точкой юга, а звезда β малой медведицы — к северу от зенита на расстоянии в 24°48′. Чему равно склонение этих звезд?
Задача 72.Какое склонение имеют звезды, которые в верхней кульминации в Канберре (φ = —35°20′) находятся на зенитном расстоянии 63°39′ к северу от зенита и на высоте +58°42′ над точкой юга?
Задача 73.В Душанбе звезда Капелла (α Возничего) проходит верхнюю кульминацию на высоте +82°35′ при азимуте 180°, а звезда Альдебаран (α Тельца), склонение которой +16°25′, — на зенитном расстоянии 22°08′ к югу от зенита. Чему равно склонение Капеллы?
Задача 74.Вычислить склонение звезд δ Большой медведицы и Фомальгаута (α Южной Рыбы), если разность зенитных расстояний этих звезд и Альтаира (α Орла) в верхней кульминации в Ташкенте (φ=+41°18′) составляет соответственно —48°35′ и +38°38′. Альтаир кульминирует в Ташкенте на высоте +57°26′ над точкой юга.
Задача 75.Какое склонение у звезд, кульминирующих на горизонте и в зените Тбилиси, географическая широта которого + 41°42′? Рефракцию в горизонте принять 35′.
Задача 76.Найти прямое восхождение звезд, в моменты верхней кульминации которых звездные часы показывали 18ч25м32с и 19ч50м40с, если при их показании 19ч20м16с звезда Альтаир (α Орла) с прямым восхождением 19ч48м21с пересекла небесный меридиан к югу от зенита.
Задача 77.В момент верхней кульминации Солнца его прямое восхождение было 23ч48м09с, а звездные часы показывали 23ч50м01с. За 46м48с до этого небесный меридиан пересекла звезда β Пегаса, а при показаниях тех же часов 0ч07м40с наступила верхняя кульминация звезды α Андромеды. Какое прямое восхождение у этих двух звезд?
Задача 78.27 октября 1975 г. в Одессе Марс прокульминиро-вал через 15м50с по звездным часам после звезды Бе-тельгейзе (α Ориона) на высоте, превышающей высоту этой звезды в кульминации на 16°33′, Прямое восхождение Бетельгейзе 5ч52м28с и склонение +7°24′. Какие экваториальные координаты были у Марса и вблизи какой точки эклиптики он находился?
Задача 79.24 августа 1975 г. в Москве (φ = +55°45′), когда звездные часы показывали 1ч52м22с, Юпитер пересек небесный меридиан на зенитном расстоянии 47°38′. В 2ч23м31с по тем же часам прокульминировала звезда α Овна, прямое восхождение которой 2ч04м21с Чему были равны экваториальные координаты Юпитера?
Задача 80.В пункте с географической широтой +50°32′ полуденная высота Солнца 1 мая и 11 августа равнялась + 54°38′, а 21 ноября и 21 января +19°29′. Определить экваториальные координаты Солнца в эти дни.
Задача 81.В истинный полдень 4 июня 1975 г. Солнце прошло в Одессе (φ = +46°29′) на высоте +65°54′, а за 13м44с до этого звезда Альдебаран (α Тельца) пересекла небесный меридиан на зенитном расстоянии, превышающем полуденное зенитное расстояние Солнца на 5°58′. Определить экваториальные координаты Солнца и звезды.
Задача 82.28 октября 1975 г. в 13ч06м41с по декретному времени в пункте с λ = 4ч37м11с (n=5) и φ=+41°18′ зенитное расстояние Солнца было 54°18′. За 45м45с (по звездному времени) до этого в верхней кульминации находилась звезда Спика (α Девы), а через 51м39с после нее — звезда Арктур (α Волопаса) на высоте +68°01’ю. Определить экваториальные координаты Солнца и Арктура. Уравнение времени в этот день было — 16м08с.
Задача 83.Найти географическую широту местности, в которой звезды β Персея (δ = +40°46′) и ε Большой Медведицы (δ = +56°14′) в моменты верхней кульминации находятся на одинаковом зенитном расстоянии, но первая — к югу, а вторая — к северу от зенита.
Задача 84.В моменты верхней кульминации звезда α Гончих Псов со склонением +38°35′ проходит в зените, звезда β Ориона — на 46°50′ южнее, а звезда α Персея — на 11°06′ севернее. На какой географической параллели проведены измерения и чему равно склонение указанных звезд?
Задача 85.В момент верхней кульминации Солнца средний хронометр показал 10ч28м30с, а при его показании 14ч48м52с был принят из Гринвича 12-часовой радиосигнал точного времени. Найти географическую долготу места наблюдения, если уравнение времени в этот день было +6м08с.
Задача 86.В момент верхней кульминации звезды ι Геркулеса на зенитном расстоянии в 2°14′ к северу от зенита звездное гринвичское время было 23ч02м39с. Экваториальные координаты ι Геркулеса α=17ч38м03- и δ = +46°02′, Определить географические координаты места наблюдения.
Задача 87.В момент показания звездного хронометра 18ч07м27с экспедиция приняла радиосигнал точного времени, переданный из Гринвича в 18ч0м0с по звездному гринвичскому времени. В момент верхней кульминации звезды γ Кассиопеи на зенитном расстоянии в 9°08′ к югу от зенита показание того же хронометра было 19ч17м02с. Экваториальные координаты γ Кассиопеи α = 0ч53м40с и δ = +60°27′. Найти географические координаты экспедиции.
Задача 88.В истинный полдень показание среднего хронометра экспедиции было 11ч41м37с, а в момент приема 12-часового радиосигнала точного времени из Москвы тот же хронометр показал 19ч14м36с. Измеренное зенитное расстояние звезды α Лебедя (δ = +45°06′) в верхней кульминации оказалось равным 3°26′ к северу от зенита. Определить географические координаты экспедиции, если в день проведения наблюдений уравнение времени равнялось —5м 17с.
Задача 89.В истинный полдень штурман океанского лайнера измерил высоту Солнца, оказавшуюся равной +75°41′ при азимуте 0°. В этот момент средний хронометр с поправкой — 16м,2 показывал 14ч12м,9 гринвичского времени. Склонение Солнца, указанное в морском астрономическом ежегоднике, было +23°19′, а уравнение времени +2м55с. Какие географические координаты имел лайнер, где и в какие примерно дни года он в это время находился?
Ответы — Практическое определение географических и небесных экваториальных координат
Преобразование небесных координат и систем счета времени. Восход и заход светил
Связь между горизонтальными и экваториальными небесными координатами осуществляется через параллактический треугольник PZM (рис. 3), вершинами которого служат полюс мира Р, зенит Ζ и светило M, а сторонами — дуга ΡΖ небесного меридиана, дуга ΖΜ круга высоты светила и дуга РМ его круга склонения. Оче видно, что ΡΖ=90°—φ, ZM = z = 90°—h и PM=90°—δ, где φ — географическая широта места наблюдения, z — зенитное расстояние, h — высота и δ — склонение светила.
В параллактическом треугольнике угол при зените равен 180°—A, где A — азимут светила, а угол при полюсе мира — часовому углу t того же светила. Тогда горизонтальные координаты вычисляются по формулам

sin z · cos A = — sin δ · cos φ+cos δ · sin φ · cos t, (29)
sin z · sin A = cos δ · sin t, (30)
а экваториальные координаты — по формулам
sin δ = cos z · sin φ — sin z · cos φ · cos A, (31)
cos δ · cos t = cos z · cos φ+sin z · sin φ · cos A, (32)
cos δ · sin t=sin z · sin A, (30)
причем t = S — α, где α — прямое восхождение светила и S — звездное время.
Рис. 3. Параллактический треугольник
При расчетах необходимо по таблице 3 переводить интервалы звездного времени ΔS в интервалы среднего времени ΔT (или наоборот), а звездное время s0 — в среднюю гринвичскую полночь заданной даты заимствовать из астрономических календарей-ежегодников (в задачах этого раздела значения s0 приводятся).
Пусть некоторое явление в каком-то пункте земной поверхности произошло в момент Τ по принятому там времени. В зависимости от принятой системы счета времени по формулам (19), (20) или (21) находится среднее гринвичское время T0, представляющее собой интервал среднего времени ΔT, протекший с гринвичской полночи (ΔT=T0). Этот интервал по таблице 3 переводится в интервал звездного времени ΔS (т. е. ΔT→ΔS), и тогда в заданный момент T соответствующий среднему гринвичскому времени T0, звездное время в Гринвиче
а в данном пункте
где λ — географическая долгота места,
Перевод интервалов звездного времени ΔS в интервалы среднего времени ΔΤ = Τ0 (т. е. ΔS→ΔT) осуществляется по таблице 3 вычитанием поправки.
Моменты времени и азимуты точек восхода и захода светил вычисляются по формулам (28), (29), (30) и (13), в которых принимается z=90°35′ (с учетом рефракции ρ = 35′).
Найденные значения часового угла и азимута в пределах от 180 до 360° соответствуют восходу светила, а в пределах от 0 до 180° — его заходу.
При вычислениях восхода и захода Солнца учитывается еще его угловой радиус r=16′. Найденные часовые углы t 
Моменты восхода и захода всех светил вычисляются с точностью, не превышающей 1м.
Преобразование небесных координат и систем счета времени – Пример 1
В каком направлении был заранее установлен телескоп с фотокамерой для фотографирования солнечного затмения 29 апреля 1976 г., если в пункте с географическими координатами λ=2ч58м,0 и φ = +40°14′ середина затмения наступила в 15ч29м,8 по времени, отличающемуся от московского на +1ч? В этот момент экваториальные координаты Солнца: прямое восхождение α=2ч27м,5 и склонение δ= + 14°35′. В среднюю гринвичскую полночь 29 апреля 1976 г. звездное время s0=14ч28м19c.
Данные: пункт наблюдения, λ = 2ч58м,0, φ = +40°14′, T=15ч29м,8, Τ—Tм=1ч; s0 = 14ч28м19c = 14ч28м,3; Солнце, α=2ч27м,5, δ = +14°35′.
Решение. В середине затмения московское время Тм = Т—1ч=14ч29м,8, и поэтому среднее гринвичское время T0 = Tм—3ч = 11ч29м,8. С гринвичской полночи прошел интервал времени ΔТ = Т0 = 11ч29м,8, который переводим по таблице 3 в интервал звездного времени ΔS=11ч31м,7, и тогда в момент T0, по формуле (33), звездное время в Гринвиче
S0=s0+ΔS = 14ч28м,3 + 11ч31м,7 = 25ч60м = = 2ч0м,0
а в заданном пункте, по формуле (14), звездное время S = S0+λ=2ч0м,0 + 2ч58м,0 = 4ч58м,0
и, по формуле (13), часовой угол Солнца
t = S—α = 4ч58м, 0—2ч27м, 5 = 2ч30м, 5,
или, переводя по таблице 1, t = 37°37′,5
37°38′. По таблицам тригонометрических функций находим:
sin φ = sin 40°14′ = +0,6459,
cos φ = cos 40°14′ = +0,7634;
sin δ = sin 14°35′ = +0,2518,
cos δ = cos 14°35′ = +0,9678;
sin t = sin 37°38′ = +0,6106,
cos t = cos 37°38′ = +0,7919.
По формуле (28) вычисляем
cos z = 0,6459 · 0,2518 + 0,7634 · 0,9678 · 0,7919 = = +0,7477
и по таблицам находим z = 41°36′ и sin z = +0,6640. Для вычисления азимута используем формулу (30):
откуда получаем два значения: A = 62°52′ и A = 180° — 62°52′ = 117°08′. При δ
Источник

