Как найти гравитационную постоянную луны
В данной главе мы рассмотрим, как Луна воздействует своим гравитационным полем собственно на саму Землю, т.е. на ее тело и ее движение по орбите. Последствия данного воздействия для различных земных сфер — литосферы, гидросферы, ядра, атмосферы, магнитосферы и др., а также для биосферы будут рассмотрены в следующих главах.
ВНИМАНИЕ!
Графики гравитационного взаимодействия Луны и Земли см. с помощью сервиса
ЛУННЫЙ ФАКТОР
3.1. ПАРАМЕТРЫ ЛУННОЙ ГРАВИТАЦИИ.
Расчетные соотношения и константы
Для расчета гравитационного воздействия Луны воспользуемся формулой классической физики, определяющей силу F взаимного притяжения двух тел с массами M1 и M2, центры масс которых находятся друг от друга на расстоянии R:
(1) F (н) = (G x M1 x M2) / R 2 ,
где G = 6,67384 х 10 -11 — гравитационная постоянная.
Данная формула дает значение силы притяжения в единицах системы СИ — ньютонах (н). Для целей нашего трактата удобнее и понятнее будет оперировать килограммами силы (кгс), которые получаются делением F на коэффициент 9,81, т.е.:
(2) F (кгс) = (G x M1 x M2) / (9,81 х R 2 )
Для дальнейших расчетов нам потребуются следующие константы:
- масса Луны — 7,35 х 10 22 кг;
- среднее расстояние от Земли до Луны — 384400 км;
- средний радиус Земли — 6371 км;
- масса Солнца — 1,99 х 10 30 кг;
- среднее расстояние от Земли до Солнца — 149,6 млн. км;
Сила лунного притяжения на Земле
В соответствии с формулой (2), сила притяжения Луной тела массой 1 кг, находящегося в центре Земли, при расстоянии между Луной и Землей, равном его среднему значению, равна:
(3) F = (6,67 х 10 -11 х 7,35 х 10 22 х 1) / (9,81 х 384400000 2 ) = 0, 000003382 кгс
т.е. всего 3,382 микрограмма. Для сравнения расчитаем силу притяжения того же тела Солнцем (также для среднего расстояния):
(4) F = (6,67 х 10 -11 х 1,99 х 10 30 х 1) / (9,81 х 149600000000 2 ) = 0, 000604570 кгс,
т.е. 604,570 микрограмм, что почти в 200 (двести!) раз больше, чем сила притяжения Луной.
Кроме того, вес тела, находящегося на поверхности Земли, изменяется в гораздо более существенных пределах из-за отклонения формы Земли от идеальной, неравномерности рельефа и плотности, а также влияния центробежных сил. Так, например, вес тела массой в 1 кг на полюсах больше веса на экваторе примерно на 5,3 грамма, причем одна треть этой разницы обусловлена сплюснутостью Земли с полюсов, а две трети — центробежной силой на экваторе, направленной против силы тяжести.
Как видно, прямое гравитационное воздействие Луны на конкретное тело, находящееся на Земле, является в прямом смысле микроскопическим и при этом существенно уступает гравитационному воздействию Солнца и геофизических аномалий.
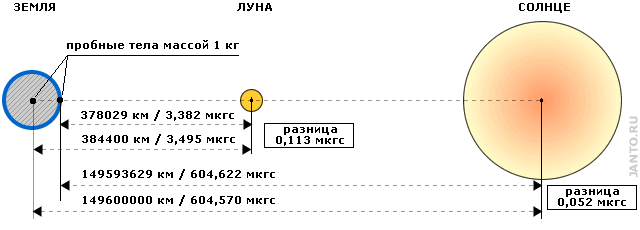
Градиент силы лунного притяжения
Обратимся к рис.3.1. Для среднего значения расстояния Земля — Луна сила притяжения Луной тела массой 1 кг, расположенного на поверхности Земли в ближайшей к Луне точке составляет 3,495 микрограмм, что на 0,113 микрограмм больше, чем сила притяжения того же тела, но расположенного в центре Земли. Сила же притяжения тела, находящегося на поверхности Земли, Солнцем (также для среднего значения расстояния) составит 604,622 микрограмма, что больше силы притяжения того же тела, но расположенного в центре Земли, на 0,052 микрограмма.
Рис.3.1 Лунная и солнечная гравитация
Т.о, несмотря на неизмеримо меньшую массу Луны по сравнению с Солнцем, градиент силы ее тяготения на орбите Земли в среднем в два с лишним раза больше градиента силы тяготения Солнца.
3.2. ВЛИЯНИЕ НА ТЕЛО ЗЕМЛИ
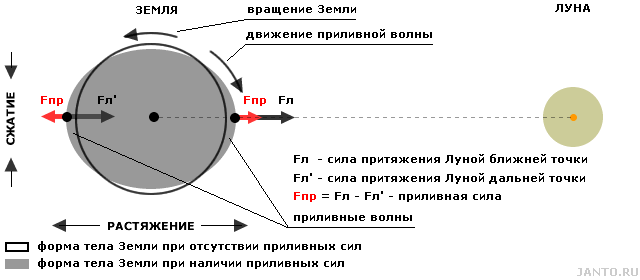
Для иллюстрации воздействия гравитационного поля Луны на тело Земли обратимся к рис. 3.2.
Рис.3.2 Влияние гравитационного поля Луны на тело Земли.
Данный рисунок представляет весьма и весьма упрощенную картину реакции тела Земли на воздействие лунной гравитации, но достоверно отражает суть процесса — изменение формы земного шара под воздействием т.н. приливных (или приливообразующих) сил, направленных вдоль оси Земля — Луна, и противодействующих им сил упругости тела Земли. Приливные силы возникают из-за того, что точки Земли, расположенные ближе к Луне, притягиваются к ней сильнее, чем точки, расположенные дальше от нее. Иными словами, деформация тела Земли является следствием градиента силы притяжения Луны и противодействующих ему сил упругости тела Земли. В результате действия этих сил размер Земли увеличивается в направлении действия приливных сил и уменьшается в поперечном направлении, вследствие чего на поверхности образуется волна, именуемая приливной. Эта волна имеет два максимума, находящиеся на оси Земля — Луна и перемещающиеся по поверхности Земли в направлении, противоположном направлению ее вращения. Амплитуда волны зависит от широты местности и текущих параметров орбиты Луны и может достигать нескольких десятков сантиметров. Максимальное значение она будет иметь на экваторе при прохождении Луной ее перигея.
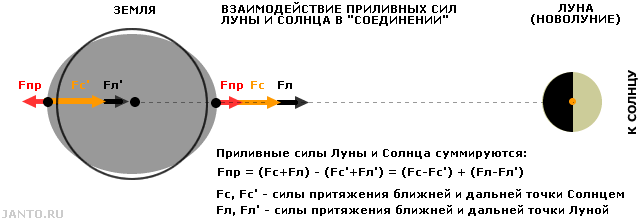
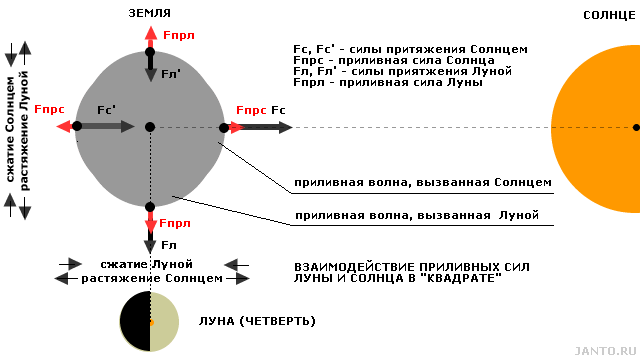
Солнце также вызывает приливную волну в теле Земли, но существенно меньшую из-за меньшего градиента силы его тяготения. Совместное гравитационное воздействие Луны и Солнца на тело Земли зависит от их взаимного расположения. Максимально значение приливных сил и, соответственно, максимальная амплитуда приливной волны достигается при расположении всех трех объектов на одной оси, т.е. в состоянии т.н. сизигии (выравнивания), что имеет место при новолунии (Луна и Солнце в «соединении») или при полнолунии (Луна и Солнце в «оппозиции»). Данные конфигурации иллюстрируются рис. 3.3 и 3.4.
Рис.3.3 Совместное влияние гравитационных полей Луны и Солнца на тело Земли
в «соединении» (в новолуние).
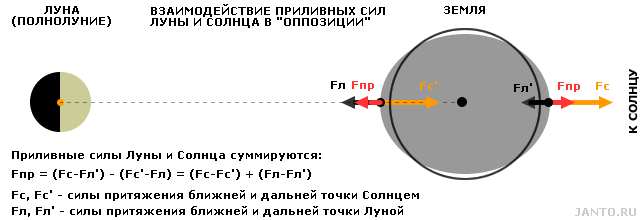
Рис.3.4 Совместное влияние гравитационных полей Луны и Солнца на тело Земли
в «оппозиции» (в полнолуние).
По мере отклонения Луны и Солнца от линии сизигии вызываемые ими приливные силы и, соответственно, приливные волны начинают приобретать самостоятельный характер, их сумма уменьшается, а степень их противодействия друг другу растет. Противодействие достигает максимума, когда угол между направлениями на Луну и Солнце из центра Земли равен 90°, т.е. данные тела находятся в «квадрате», а Луна, соответственно, находится в фазе четверти (первой или последней). В этой конфигурации приливные силы Луны и Солнца действуют на форму тела Земли строго противоположно, соответствующие приливные волны на поверхности максимально разнесены, а их амплитуда минимальна, что иллюстрируется рис. 3.5.
Рис.3.5 Совместное влияние гравитационных полей Луны и Солнца на тело Земли в «квадрате».
Примечание. «Соединение», «оппозиция», «квадрат» (или «квадратура») — термины, используемые в астрономии и астрологии для определения геометрии взаимного расположения двух небесных тел или точек относительно Земли. Подробнее см. Лунные аспекты.
Физика земных приливных процессов под воздействием гравитационных полей Луны и Солнца весьма сложна и требует учета большого числа параметров. На эту тему было разработано большое число различных теорий, проведено много экспериментальных исследований, написано огромное количество статей, монографий и диссертаций. Даже на сегодняшней день в этой области остается много «белых» пятен, противоречащих друг другу точек зрения и альтернативных подходов. Для желающих углубиться в проблематику земных приливов можно рекомендовать фундаментальное исследование П. Мельхиора «Земные приливы» (пер. с англ., М., «Мир», 1968 г. 483 страницы).
3.3. ВЛИЯНИЕ НА ОРБИТУ ЗЕМЛИ
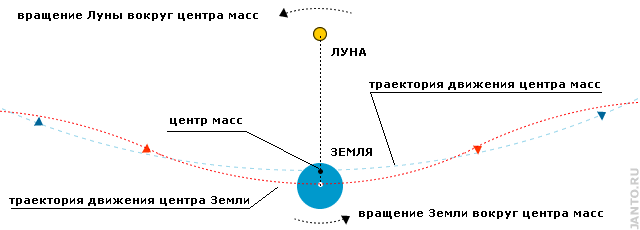
Как было отмечено в п.1.1 главы 1, Луна для естественного спутника планеты обладает аномально большой массой, поэтому более корректно считать, что Земля и Луна образуют двойную планетную систему, вращающуюся вокруг общего центра масс, который смещен относительно центра Земли в среднем на 4670 км. Вследствие этого Земля, вращаясь вокруг своей центральной оси, одновременно вращается и вокруг этого центра масс с периодом, равным синодическому лунному месяцу, т.е. 29,530588 солнечных суток. В результате на эллиптическую орбиту Земли накладывается переменнная «модулирующая» составляющая с соответствующей амплитудой и периодом (см. рис.3.6).
Рис.3.6 Модуляция орбиты Земли лунной гравитацией
Эта составляющая изменяет расстояние от Земли до Солнца, что приводит к колебаниям солнечной гравитации примерно на ± 450 мкгс, практически не влияя на ее градиент. Кроме того, она создает определенные силы инерции, внося дополнительный вклад в изменение силы тяжести в зависимости от положения тела на поверхности Земли, а также незначительно влияет на величину достигающей Земли солнечной энергии (см. здесь).
3.4. КРАТКОЕ РЕЗЮМЕ
Следствием воздействия лунной гравитации на Землю являются два фундаментальных явления:
- Лунные приливы на поверхности Земли — периодических изменений уровня земной поверхности, синхронизированные с суточным вращением Земли и перемещением Луны по орбите.
- Наложение на земную орбиту переменной составляющей, синхронизированной с вращением системы Земля — Луна вокруг общего центра масс.
Данные явления являются главными механизмами воздействия Луны на земные сферы — литосферу, гидросферу, земное ядро, атмосферу, магнитосферу и др. Более подробно об этом — в следующей главе.
Источник
Гравитационная Постоянная. Массы Земли, Луны, Солнца.
Гравитационная константа может по праву считаться самой старой физической константой. Казалось бы, что сейчас она должна быть одной из наиболее точных констант.
Эх, как хотелось бы!
Но, увы!
Точность гравитационной постоянной в последние годы скачет.
До 1999 года предлагаемый диапазон её значений был: (6.67174 — 6.67344)·10 -11 м 3 кг -1 c -2 ,
с 1999 года её точность упала на два порядка: (6.663 — 6.683)·10 -11 м 3 кг -1 c -2 ,
с 2002 года её уточнили на порядок: (6.6732 — 6.6752)·10 -11 м 3 кг -1 c -2 ,
с 2006 года её ещё уточнили: (6.67361 — 6.67428)·10 -11 м 3 кг -1 c -2 .
Это же можно записать короче:
до 1999 года G=6.67259(85)·10 -11 м 3 кг -1 c -2 ,
с 1999 года G = 6.673(10)·10 -11 м 3 кг -1 c -2 ,
с 2002 года G = 6.6742(10)·10 -11 м 3 кг -1 c -2 ,
с 2006 года G = 6.67428(67)·10 -11 м 3 кг -1 c -2 .
Я малость ленив, и в этой работе я не пишу цифры в скобках, а просто подчеркиваю сомнительные цифры в числах, к примеру, так: В 1999 году точность G упала от четырех верных знаков 6.67259·10 -11 м 3 кг -1 c -2 , до двух верных знаков 6.673·10 -11 м 3 кг -1 c -2 .
Что же произошло с гравитационной константой? Развитие космонавтики? Космические корабли не вписываются в расчетные траектории? Не склеились какие-то расчеты? На самом деле, 1999 год здесь указан чисто символически. Просто в 1999 году CODATA внёс «уточнение» в рекомендованное значение гравитационной постоянной, а причиной этого «уточнения» послужили эксперименты, проведенные в разных лабораториях мира, которые дали сильно отличающиеся результаты. К примеру, группа немецких физиков под руководством W.Michaelis получила значение G на 0.6% больше принятого. Марк Фитцжеральд с сотрудниками определили G, которое оказалось на 0.1% ниже. Группа российских физиков [В.П. Измайлов, О.В. Карагиоз, В.А. Кузнецов, В.Н. Мельников, А.Е. Росляков. Measurement Techniques 36, 1065 (1993)] указали на наличие странных вариаций в G до 0.7%.
The Controversy over Newton’s Gravitational Constant
Precise Calibration of the Intrinsic Strength of Gravity and Measuring the Mass of the Earth
Вместе с изменением точности гравитационной константы изменяется точность масс планет. Так, до 1999 года на web-сайте ASTROPHYSICAL CONSTANTS http://pdg.lbl.gov/ мы видели следующие значения для гравитационной константы, масс Солнца и Земли:
G = 6.67259(85)·10 -11 м 3 кг -1 c -2 ,
MSun = 1.98892(25)·10 30 кг,
MEarth = 5.97370(76)·10 24 кг;
то с 1999 по 2002 было:
G = 6.673(10)·10 -11 м 3 кг -1 c -2 ,
MSun = 1.9889(30)·10 30 кг,
MEarth = 5.974(9)·10 24 кг.
с 2002 по сегодня (апрель 2006):
G = 6.673(10)·10 -11 м 3 кг -1 c -2 ,
MSun = 1.98844(30)·10 30 кг,
MEarth = 5.9723(9)·10 24 кг.
А если взглянуть на один из сайтов NASA http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html , то для масс Солнца и Земли мы увидим значения (2006):
MSun = 1 989 100·10 24 кг,
MEarth = 5.9736·10 24 кг.
Возникает вопрос: «А для какого G верны эти значения масс?» Очевиден ответ: «Истину сейчас нужно искать не в G и не в M, а в произведении GM. Так, на сайте NASA мы видим:
GMSun = 132 712·10 6 км 3 /с 2 ,
GMEarth = 0.3986·10 6 км 3 /с 2 .
Зато на сайте ASTROPHYSICAL CONSTANTS мы находим очень точные комбинации, содержащие произведение GM, а именно, шварцшильдовские радиусы Солнца и Земли (2GM/c 2 ):
2GMSun/c 2 = 2.95325008 км,
2GMEarth/c 2 = 8.87005622 мм.
Точность последних величин удивляет. Никто конечно Землю и Солнце не превращал в черные дыры, но очевидно, что шварцшильдовские радиусы получены не через массы и гравитационную константу, а через правую сторону закона Кеплера, содержащую период обращения спутника по орбите и её большую полуось. А последние величины действительно можно измерить с высокой точностью. Тем не менее, двум последним цифрам в этих значениях лично я не доверяю. (Ниже мы получим шварцшильдовские радиусы, чуть-чуть отличающиеся от приведенных, а пока вернемся к гравитационной константе.)
А не получить ли нам теоретическое значение гравитационной константы? Это делается элементарно. Можно даже получить не одну, а две, три, десять G. Красота. Но вот проблема. А какая же из них ближе к истине. Оставим сомнения пока в стороне. Время покажет, стоило ли это делать. Приведем несколько выводов G.
Один из выводов достаточно точного значения G был получен мной в феврале этого года (2006) и я его помещу чуть ниже. А здесь поместим вывод гравитационной константы, полученный мной в 2001 году. Назовем его метод G-2001. Замечание: в 2001 году фундаментальные константы (e, m. ) имели значения, чуть-чуть отличающиеся от сегодняшних. Перерасчет в связи с этим я не делаю, а оставляю результаты такими какими они были в 2001 году.
Вывод гравитационной константы «Метод G-2001» и массы Солнца, Земли, Луны.
Текст от 1 апреля 2001 года: Подойдем к этой проблеме гравитационной константы другой стороны. Может быть, G действительно испытывает значительные вариации. Может быть, это связано с распространением гравитационных волн длиной в несколько дней. А в этой работе, кстати, предсказан максимум гравитационных колебаний длиной волны порядка 6 световых дней. Этот максимум есть зеркальное отражение относительно граничной частоты между фотоном и гравитоном. Этот максимум, по моему убеждению, ответственен за наличие циклонов и антициклонов, за периодичность в изменении погоды. См. Пространственно- временная симметрия. Тем не менее, среднестатистическое значение гравитационной постоянной должно быть очень точным.
В настоящей работе развиты Нормированные Единицы, в которых граничная частота n 0, граничная длина волны l 0, граничный период колебаний t0 приняты равными единицам. Гравитационная постоянная в нормированных единицах безразмерна, обозначена той же буквой G, но со штрихом G’, и может быть получена по формулам:
если определяющая гравитирующая частица — протон то
1. G’ = Gt0 2 mpr/ l 0 3 = 3.0398508967·10 -60 ,
2. G’ = N(fgr/fel)pr-el/(2 p 2 ) = 3.0398508967·10 -60 ,
3. G’ = ( a/e 0/G) 1/2 e/mel/2 = 3.0398508967·10 -60 ,
4. G’ = 1/Exp( a +1/ a ) = 3.0398508967·10 -60 ;
если определяющая гравитирующая частица — атом водорода то
1. G’ = Gt0 2 mH/ l 0 3 = 3.043933809·10 -60 ,
2. G’ = N(fgr/fel)H-el/(2 p 2 ) = 3.043933809·10 -60 ,
3. G’ = ( a/e 0/G) 1/2 e/mel/2 = 3.043933809·10 -60 ,
4. G’ = 1/( s Exp(1/ a )) = 3.062114896E-60 / s = 3.043933809·10 -60 .
Последние результаты, полученные в январе феврале 2001 года, показали, что второй вариант, где определяющей гравитирующей частицей является атом водорода, оказывается предпочтительней. Поэтому, далее мы исследуем именно второй вариант. Но что же прячется за буквой s в последней формуле. В случае протона, как определяющей частицы, мы вводили релятивистскую поправку в формулу G’ = 1/Exp(1/ a ). В результате формула изуродовалась, а её хорошее приближение приобрело вид G’ = 1/Exp( a +1/ a ). В случае с водородом этого делать не хочется, и мы попробуем поискать, а что же должно быть на месте s ?
Отношение 3.062114896·10 -60 / 3.043933809·10 -60 = 1.0059730 = s .
Отношение ln(1/G’) / (1/ a ) = 1.00004345664 = 1 + a ln( s ).
Разложим по полочкам приведенные выше формулы, содержащие G’.
G’ — гравитационная константа в нормированных единицах, безразмерна; точнее — сократимая комбинация вспышек: [!ОБ/пр], [!/!];
G — гравитационная константа в метрических единицах размерная: [Н·м 2 /кг 2 ] или [м 3 /кг/c 2 ];
mH — масса атома водорода; mH = 1,67·10 -27 кг в метрических единицах, или mH = 1 нормированных единиц массы;
n 0, l 0, t0 — граничные величины (частота, длина волны, период) между фотоном и гравитоном, или между электромагнитными и гравитационными волнами. Эти же величины являются коэффициентами перехода от нормированных величин к метрическим.
Пример 1: L = 3000 метров, L’ = L/ l 0 = 3000м / 408181м/! = 0.00735! То есть, 3000 метров приближенно равно 0.00735 вспышек.
Пример 2: T = 3000 секунд, T’ = T/t0 = 3с / 0.00136с/! = 2203! То есть, 3 секунды приближенно равно 2203 вспышек.
Пример 3: G = 6.672606660·10 -11 м 3 /кг/c 2 , G’ = Gt0 2 mH/ l 0 3 = 3.043933809·10 -60 .
Итак, простейший смысл первой из приведенных формул заключается в обычном переводе G из метрических единиц в нормированные. Более глубокий смысл этой формулы заключается в приведении этой формулы к третьему закону Кеплера
Эти формулы связывают электромагнитные и гравитационные взаимодействия и являются просто разной формой записи одного и того же, то есть, это не система из двух уравнений. В эти формулы входят следующие величины:
N — Число Инерциальных Систем Отсчета в точке для mH; N — размеры Вселенной в нормированных единицах; N — число уровней энергии нормированной единицы массы mH в пространстве. Единицы измерения частное от вспышек разного уровня: вспышек на оборот; !/об; вспышка нашего масштаба на вселенскую вспышку. Вспышка есть акт пространственно-временной синхронизации. N определяется через решение одного из уравнений N = sqr(mHc 2 /(hH)), N = sqr( ap (fel/fgr)el-el), где fel/fgr)e-e отношение электрических сил к гравитационным между двумя электронами.
(fgr/fel)H-el — эту величину в случае, если определяющей массой является атом водорода, не назовешь отношением сил между атомом водорода и электроном. Лучше сказать, что это комбинация констант: (fgr/fel)H-el = (GmHmel/R 2 ) / (e 2 /(4 pe 0R 2 )) = (GmHmel) / (e 2 /(4 pe 0)) = 4 pe 0GmHmel/e 2 . (Последнее является слабым местом в выборе между протоном и атомом водорода на роль определяющей массы частицы во Вселенной.)
Формула 4: 1/G’ = s Exp(1/ a )
Эмпирическая формула. Так действительно должно быть. Гравитация и электромагнетизм симметричны друг другу. И это находит своё отражение в связи между безразмерными константами электрического и гравитационного взаимодействия. Форма записи была бы изумительна без корявого коэффициента s . (Вспомним лямбда-коэффициент ОТО.) Поэтому, a есть постоянная тонкой структуры электромагнитных взаимодействий, а G’ есть постоянная тонкой структуры гравитационных взаимодействий.
Итак, нам еще предстоит выяснить, что же такое:
ln(1/G’) / (1/ a ) = 1.00004345664 = 1 + a ln( s ), или
(1/Exp(1/ a )) / G’ = 3.062114896·10 -60 / 3.043933809·10 -60 = 1.0059730 = s .
Массы Земли, Луны, Солнца
Здесь мы попытаемся получить массы Земли, Луны, Солнца несколько нетрадиционным способом. Прежде всего, укажем, что эти массы сильно отличаются от справочника к справочнику. Поместим значения из разных справочников в таблицу. В последнюю колонку, красным цветом я ввожу свои данные, которые мы получим ниже, при условии нескольких «ЕСЛИ». То есть, результаты верны, ЕСЛИ такие-то предположение верны. А сначала в таблице идут значения, приведенные в современных справочных сайтах по состоянию на март 2001 года.
1. http://pdg.lbl.gov/
2. http://www.seds.org/nineplanets/nineplanets/earth.html
3. http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html
4. «устаревшие значения» из энциклопедического словаря по физике за 1983 год, который переиздан в 1999 году.
5. Мои результаты (2001).
| . | 1 | 2 | 3 | 4 | 5 (если. ) |
| MEarth (*10 24 кг) | 5.974(9) | 5.972 | 5.9736 | 5.976 | 5.973538542 |
| MMoon (*10 22 кг) | — | 7.35 | 7.349 | 7.35 | 7.3463 |
| MSun (*10 30 кг) | 1.9889(30) | 1.989 | 1.9891 | 1.989 | 1.988909058 |
| LSun (*10 26 Вт) | 3.846(8) | 3.86 | 3.846 | 3.826 | 3.841740089 |
| GMSun (*10 17 м 3 /с 2 ) | — | — | 1.32712 | — | 1.327120783 |
| 2GMSun /c 2 (км) | 2.95325008 | — | — | — | 2.953242026 |
| GMEarth (*10 14 м 3 /с 2 ) | — | — | 3.986 | — | 3.985907306 |
| 2GMEarth /c 2 (мм) | 8.87005622 | — | — | — | 8.869839976 |
Давайте попытаемся постулировать следующие утверждения:
Мир предельно симметричен. Для того, чтобы на планете Земля в Солнечной системе развилась разумная жизнь необходимо чтобы: Солнце миллиарды лет имело неизменную мощность, строго определяемую по формуле L = GMSun 2 H/(4 l 0). А Земля должна миллиарды лет занимать одну и ту же резонансную орбиту с квантовым числом пять, точно. Следовательно, формула H = GMEarth/(5r) 2 /c верна точно. Пятерка несколько раз входит в качестве простого множителя в отношение сил между электронами, то есть, гипотеза «(fgr/fel)electron-electron = 2.4·10 -43 точно» верна. Следовательно, N = 10 22 ( ap /24) 1/2 = 3.090665321·10 20 (точность зависит только от a ).
А через N, по формуле Gtheory = e 2 a /(4 e 0N 2 mel 2 ) мы уточняем гравитационную константу 1986 года на 4 знака, или G1999 уточняем на 6 знаков:
G1999 = 6.673·10 -11 м 3 кг -1 c -2 .
G1986 = 6.67259·10 -11 м 3 кг -1 c -2 .
Gtheory = 6.672606660·10 -11 м 3 кг -1 c -2 .
По формуле H = c 2 mH / (N 2 h) получим константу Хаббла:
H = 2.376378745E-18 об/секунду, или, поскольку 1 парсек = 3.0856775807E+16 метров, то: H = 73.32738618 км/с/Мпк. (Результат «Ключевого Проекта» на телескопе Хаббла дал: 72 = +/- 8 km/s/Mpc )
По формуле MEarth = 5 2 r 2 Hc/G, где: r — большая полуось земной орбиты, получим массу Земли (r = 149597870660 м):
MEarth = 5.973538542·10 24 кг.
GMEarth = 3.985907306·10 14 м 3 /с 2 .
С Луной дело обстоит сложнее. Точное квантовое резонансное число для неё пока не найдено (март, 2001). Получается нечто вроде 216, но не точно! Заметим что 216=6 3 . Кроме того, известно, что MEarth / MMoon
81 = 3 4 . Но это опять же не точно.
На странице Moon Fact Sheet мы находим отношение масс Луны и Земли: 0.0123, или мы можем записать: 0.0123 =1/81.3008. Или читаем у П.И. Бакулина «Курс Общей Астрономии» стр.105:». По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось равным 1/81.30. » Это будет 0.01230012. А на странице http://www.solarviews.com/eng/moon.htm мы находим, что это отношение равно 0.012298. А радиус орбиты: 384403 км. Можно ли доверять этой страничке? Бог знает. Рискнём. Сомнительные цифры для Луны мы жирно подчеркнём. Пусть MMoon / MEarth = 0.012298. Тогда:
MMoon = 7.3463·10 22 кг.
Теперь найдем массу Солнца, пользуясь законом Кеплера. G(M+m)/(4 p 2 )= a 3 /T 2 ,где a = 149597870660 метров, — большая полуось земной орбиты, или астрономическая единица; T = 31558149.8 секунд = 365.256 дней — сидерический год. (Сидерический год: от фиксированной звезды до фиксированной звезды; тропический год от эквинокса до эквинокса, точки весеннего равноденствия).
В левой части закона Кеплера стоит две массы. Но мы то знаем, что там стоит не две массы, а пять масс, которые можно представить как два тела. Первое тело, — это Солнце и внутренние планеты: Меркурий и Венера. А второе тело, — это система Земля-Луна. Подставляя все эти массы в закон Кеплера, мы уменьшаем массу Солнца в шестом-седьмом знаке и чуть-чуть удаляемся от «точного» результата шварцшильдовского радиуса 2GMSun/c 2 = 2.95325008 км, который мы «откопали» на сайте ASTROPHYSICAL CONSTANTS. Наша масса Солнца получается:
MSun = 1.988909058·10 30 кг.
Или совокупная внутренняя масса, влияющая на движение системы Земля Луна:
MInt = MSun + MVen + MMer = 1.988914257·10 30 кг.
Другие понятные величины:
GMSun =1.327120783·10 17 м 3 /с 2 .
GMInt = 1.327124251·10 17 м 3 /с 2 .
2GMSun/c 2 =2.953242026 км.
2GMInt/c 2 = 2.953249746 км.
Имеем в виду, что полученные результаты верны, если работают допущения » ЕСЛИ «.
Выводы гравитационной константы
«Метод G-1999», «Метод G-2006».
На моей странице Физические Константы можно увидеть, как получено нормированное (безразмерное) значение гравитационной константы G’.
Если взять логарифм от этого числа, то получим число 137.04268(22).
Сравни с постоянной тонкой структуры a =1/137.03599911(46).
А еще лучшее сходство получается для величины a +1/ a =137.04329646(46).
Поскольку G известна с малой точностью, и предполагая, что формула G’=1/Exp( a +1/ a ) верна, можно получить сначала G’, а из этого значения получим G1999_t = 6.671480(24)·10 -11 м 3 кг -1 c -2 .
Если же верна G’=1/Exp(1/ a ), то G1999_0 = 6,718976(24)·10 -11 м 3 кг -1 c -2 .
Эти результаты получены в 1999 году. Результат G1999_0 довольно сильно отличается от наблюдаемого значения гравитационной константы. Однако, если предположить, что это аналог электрической постоянной, а в закон Ньютона входит ещё и гравитационная проницаемость среды, по аналогии с электрической проницаемостью среды в законе Кулона, то различие становится не избыточным, а необходимым. Этот вариант проанализирован на странице Ядро Земли — раскаленная пустота; Объединение взаимодействий.
В феврале 2006 года было замечено еще одно свойство в семье констант.
Для того, чтобы свести данные по G к одному и тому же числу, необходимо либо увеличить массу протона в число близкое к 1.00115 3 , либо стартовую G в 1.00115 4 , либо и т.п. в 1.00115 x раз.
Что же это за число, 1.00115?
И встречалось ли оно раньше?
Магнетон Бора — это простая комбинация констант и он должен соответствовать магнитному моменту электрона.
Но согласно CODATA-2002 истинное значение магнитного момента электрона отличается от магнетона Бора в -1.0011596521859(38) раз.
Тогда можно допустить, что получаемое G’=1/Exp(1/ a ) есть «комбинация констант», а истинное значение G ослаблено в 1.0011596521859(38) x раз. Таким образом, мы получаем более точное значение для G.
Расчет дает:
G2006=6,6730102(37)·10 -11 м 3 кг -1 c -2 ,
G2009=6,6730079(15)·10 -11 м 3 кг -1 c -2 .
Наша G в 300 раз точнее, чем величина, предлагаемая CODATA2009: G=6,67428(67) · 10 -11 м 3 /(сек 2 кг).
Наш результат имеет достаточно высокую достоверность, думаю, порядка 95%. Это следует из анализа движения образа и прообраза электрона в VB-программе http://darkenergy.narod.ru/SR2007.exe Описание программы: 1, 2.
А также из анализа Exel-программы http://darkenergy.narod.ru/data.xls.
Сейчас (май 2009) стало понятно, почему магнитная аномалия элементарного заряда оказывает влияние на гравитационную константу.
В результате нормировки физических величин, все физические константы удивительно красиво выразились через число N, через постоянную тонкой структуры a , и через отношение масс протона и электрона D. Прекрасно, всего лишь три числа (N, a , D), и все константы у нас в руках! Лишь гравитационная постоянная не выражалась красиво через эти числа (N, a , D). Одна красивая формула была замечена: G’ = 1/Exp(1/ a ), но поскольку она не давала точного совпадения, раннее использовалось приближение к ней: G’ = 1/Exp( a +1/ a ). В 2006 году была найдена точная формула для вывода гравитационной константы, а в этом году 2009 она была логически обоснована. Нормированная гравитационная константа действительно может быть записана так: G» = 1/Exp(1/ a ), но измеряемая величина, которую мы назовем аномальной нормированной гравитационной константой, есть G’ = 1 / (Exp(1/ a ) δ 6 ), где : δ — отношение магнитного момента электрона к магнетону Бора. Как известно, величина δ теоретически выводится через два числа ( p и α ), следовательно, наша G» тоже выражается через эти же числа. Найдя G’ или G» , мы можем получить G :
G=ch( α G’/D 2 ) 2/3 /2 1/3 /m 2 =ch( α G»/D 2 ) 2/3 /2 1/3 /m μ 2 ,
где: c — скорость света, h — постоянная Планка, D — отношение масс протона и электрона, m — масса электрона, m μ — «аномальная масса электрона». «Аномальная масса электрона» это величина, равная сумме масс электрона и «вакуумных добавок», получаемая из равенства m μ c 2 = pB, где p — магнитный момент электрона; B — магнитная индукция, создаваемая током «вращающегося электрона». Магнитный момент электрона превосходит магнетон Бора в δ раз. Это превосходство как раз и обеспечивается «вакуумными добавками». С учетом того, что магнитный момент контура с током определяется по формуле p = IS; а магнитная индукция B = μ 0I / 2R, где в обе формулы входит один и тот же ток I, мы заключаем, что величина превосходит Боровский аналог величины pB в δ 2 раз. Учитывая также, что спиновой магнитный момент превосходит орбитальный момент в два раза, мы добавим в формулу p = IS коэффициент 2. Проделав выкладки, получим m μ c 2 = m δ 2 c 2 , или: m μ = m δ 2 . Поскольку гравитационные взаимодействия осуществляются посредством того же электрон-позитронного вакуума, и поскольку в закон Ньютона входят две массы взаимодействующих тел, то обе эти массы обретают экранировку, учитываемую в нашей гравитационной константе, содержащей либо δ 4 в коэффициенте m μ 2 , формулы G=ch( α G»/D 2 ) 2/3 /2 1/3 /m μ 2 , либо 1/ δ 6 в коэффициенте (G’) 2/3 формулы G=ch( α G’/D 2 ) 2/3 /2 1/3 /m 2 , что в сущности равноправно.
Сайт создан 10 июня 1998 г.
Эта страница создана 1 апреля 2001 года.
К другим разделам Космической Генетики
Источник