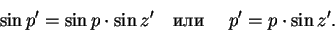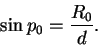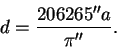Определение расстояний в Солнечной системе. Горизонтальный параллакс
Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.
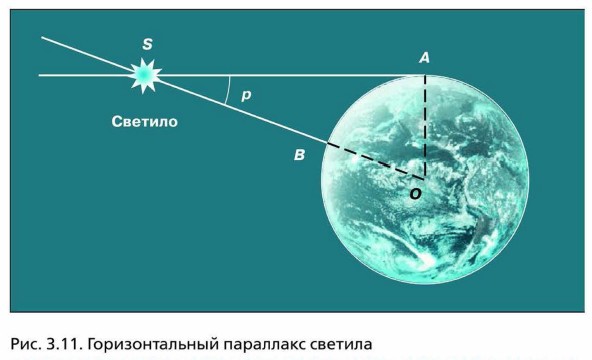
Горизонтальным параллаксом (р) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).
Из треугольника OAS можно выразить величину — расстояние OS = D:
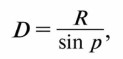
где R — радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.
Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57′. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца равен 8,8″. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 млн км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы.
Известно, что для малых углов sin р ≈ р, если угол р выражен в радианах. В одном радиане содержится 206 265″. Тогда, заменяя sin р на р и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:
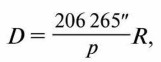
или (с достаточной точностью)
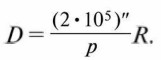
Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний — необходимое условие для расчётов траекторий полёта космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров.
Источник
Как определить параллакс солнца
Прямое определение расстояний до сравнительно близких небесных тел основано на явлении параллактического смещения. Суть его заключается в следующем. Близкий предмет при наблюдении его из разных точек проецируется на различные расположенные далеко предметы. Так, держа вертикально карандаш на фоне далекого многоквартирного дома, мы видим его левым и правым глазом на фоне разных окон. Для тел Солнечной системы такое смещение на фоне звезд заметно уже при наблюдении из точек, разнесенных на расстояние, сравнимое с радиусом Земли, а для близких звезд — при наблюдениях из точек, разнесенных на расстояние, сравнимое с радиусом орбиты Земли.
11.1. Горизонтальный экваториальный параллакс
Координаты небесных тел, определенные из разных точек земной поверхности, вообще говоря различны, и называются топоцентрическими координатами. Правда, это заметно лишь для тел Солнечной системы. Для устранения этой неопределенности все координаты тел Солнечной системы приводят к центру Земли и называют геоцентрическими. Угол между направлениями на какое-либо светило из данной точки земной поверхности и из центра Земли называется суточным параллаксом p‘ светила (рис. 22). Очевидно, что суточный параллакс равен нулю для светила, находящегося в зените, и максимален для светила на горизонте. Такой максимальный параллакс называется горизонтальным параллаксом светила p. Горизонтальный параллакс связан с суточным простым соотношением:
Здесь синусы углов заменены самими углами ввиду их малости.
По сути дела, p — это угол, под которым виден радиус Земли с данного светила. Однако Земля не является идеальным шаром и сплюснута к полюсам. Поэтому на каждой широте радиус Земли свой и горизонтальные параллаксы одного и того же светила разные. Для устранения этих различий принято вычислять горизонтальный параллакс для экваториального радиуса Земли (R0 = 6378 км) и называть его горизонтальным экваториальным параллаксом p0.
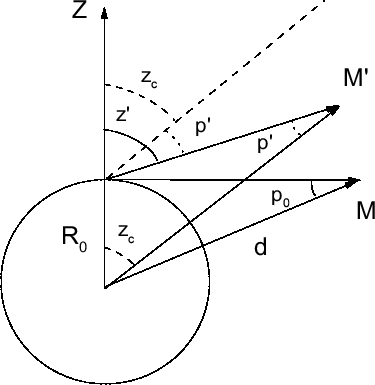 |
| Рис. 22. Суточный и горизонтальный параллакс |
Суточный параллакс необходимо учитывать при измерении высот и зенитных расстояний тел Солнечной системы и вносить поправку, приводя наблюдение к центру Земли:
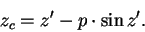 | (38) |
Измерив горизонтальный экваториальный параллакс светила p0, можно определить расстояние d до него, т.к.
Заменив синус малого угла p0 значением самого угла, выраженным в радианах, и имея в виду, что 1 радиан равен 206265″, получим искомую формулу:
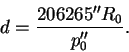 | (39) |
Замена синуса угла самим углом допустима, так как наибольший из известных горизонтальный экваториальный параллакс Луны равен 57′ (у Солнца p0=8″.79).
В настоящее время расстояния до тел Солнечной системы с гораздо большей точностью измеряются методом радиолокации.
11.2. Годичный параллакс
Угол, под которым с какой-либо звезды виден радиус земной орбиты a, при условии, что он перпендикулярен направлению на нее, называется годичным параллаксом 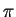
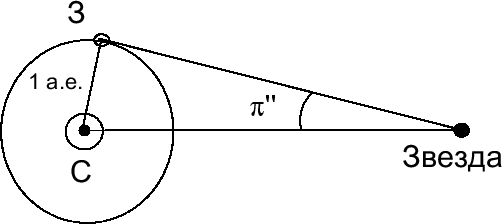 |
| Рис. 23. Годичный параллакс |
По аналогии с горизонтальным экваториальным параллаксом, зная годичный параллакс, можно определять расстояния до звезд:
В километрах расстояния до звезд измерять неудобно, поэтому обычно пользуются внесистемной единицей — парсеком пк, определяемой как расстояние, с которого параллакс равен 1″. Само название составлено из первых слогов слов параллакс и секунда. Нетрудно убедиться, что 1 пк = 206 265 а.е. = 3.086 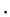
Расстояние до звезды в парсеках определяется через величину годичного параллакса особенно просто
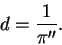 | (40) |
60. (477) Параллакс Солнца p0=8″.8, а видимый угловой радиус Солнца 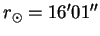
Решение: Так как параллакс Солнца есть ни что иное, как угловой радиус Земли, видимый с Солнца, следовательно, радиус Солнца во столько же раз больше радиуса Земли, во сколько его угловой диаметр больше параллакса 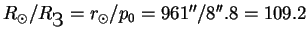
61. (482) В момент кульминации наблюденное зенитное расстояние центра Луны (p0=57′) было 50 o 00′ 00″. Исправить это наблюдение за влияние рефракции и параллакса.
Решение: За счет рефракции наблюденное топоцентрическое зенитное расстояние меньше истинного топоцентрического, т.е. 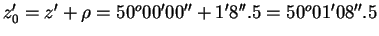
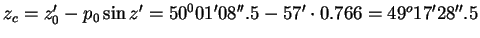
62.(472) Чему равен горизонтальный параллакс Юпитера, когда он находится от Земли на расстоянии 6 а.е. Горизонтальный параллакс Солнца p0=8″.8.
63. (474) Наименьшее расстояние Венеры от Земли равно 40 млн. км. В этот момент ее угловой диаметр равен 32″.4. Определить линейный радиус этой планеты.
64. (475) Зная, что для Луны p0=57’02».7, а ее угловой радиус в это время rЛ=15’32».6, вычислить расстояние до Луны и ее линейный радиус, выраженные в радиусах Земли, а так же площадь поверхности и объем Луны по сравнению с таковыми для Земли.
65. (483) Наблюденное зенитное расстояние верхнего края Солнца составляет 64 o 55′ 33″, а его видимый радиус 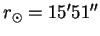
66. Из наблюдений известны годичные параллаксы 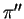
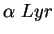
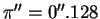
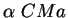
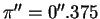
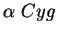
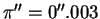
Источник
Параллакс Солнца
- Параллакс Солнца, суточный параллакс Солнца (π☉) — горизонтальный экваториальный параллакс Солнца, угол, под которым со среднего расстояния Солнца виден экваториальный радиус Земли.
До 1964 года являлся фундаментальной астрономической постоянной и считался равным 8,80″. С принятием в 1964 году астрономическим союзом новой системы единиц π☉ является производной постоянной, и составляет 8,794″.Методы определения параллакса Солнца разделяются на геометрические (тригонометрические), динамические (гравитационные) и физические.
Связанные понятия
В небесной механике механизмом, эффектом или резонансом Лидова или Лидова—Козаи называется периодическое изменение соотношения эксцентриситета и наклонения орбиты под воздействием массивного тела или тел. Либрации (колебанию около постоянного значения) подвержен аргумент перицентра.
Для большинства пронумерованных астероидов известны всего несколько физических параметров. Всего несколько сотен астероидов имеют собственные страницы в Википедии, на которых содержится название, обстоятельства открытия, таблица элементов орбиты и ожидаемые физические характеристики.
Планеты, обращающиеся около других звёзд, являются источниками очень слабого света в сравнении с родительской звездой, поэтому прямое наблюдение и обнаружение экзопланет является довольно сложной задачей. Помимо значительной сложности обнаружения такого слабого источника света возникает дополнительная проблема, связанная с тем, что яркость родительской звезды на много порядков превышает звёздную величину планеты, светящуюся отражённым от родительской звезды светом, и, тем самым, делает оптические.
Ускорение расширения Вселенной — обнаруженное в конце 1990-х годов уменьшение светимости экстремально удалённых «стандартных свечей» (сверхновых типа Ia), интерпретированное как ускорение расширения Вселенной.
Источник
Параллакс Солнца
Параллакс Солнца, суточный параллакс Солнца — горизонтальный экваториальный параллакс Солнца, угол, под которым со среднего расстояния Солнца виден экваториальный радиус Земли.
До введения в астрономическую практику радиолокационных методов определения расстояний до планет численное значение параллакса Солнца служило одной из важнейших фундаментальных астрономических постоянных, так как в сочетании с измеренным геодезическим путём экваториальным радиусом Земли оно определяло в км значение астрономической единицы, служащей масштабом всех линейных размеров во Вселенной. Методы определения параллакса Солнца разделяются на геометрические (тригонометрические), динамические (гравитационные) и физические.
Геометрические методы определения основаны на точных астрометрических измерениях положений планет относительно звёзд. Из двух обсерваторий, лежащих почти на одном меридиане и достаточно удалённых по широте, определяют склонения той или иной планеты при помощи меридианных или вертикальных кругов (см. Астрономические инструменты и приборы); таким путём вычисляют горизонтальный экваториальный параллакс планеты. Зная периоды обращений наблюдаемой планеты и Земли, на основе 3-го закона Кеплера вычисляют и искомый Параллакс Солнца. Параллаксы планет можно определить и на одной обсерватории, измеряя положения планет относительно звёзд при помощи гелиометра в различные часы суток, используя перемещение наблюдателя в пространстве вследствие суточного вращения Земли.
Начиная со 2-й половины XVII века с этой целью наблюдали Марс, приближающийся к Земле в периоды больших противостояний до 0,37 астрономической единицы (в это время параллакс Марса в 2,5 раза больше параллакса Солнца). Ещё более точными являются меридианные и гелиометрические наблюдения малых планет, положения которых на небесной сфере благодаря их звездообразному виду вычисляются более надёжно.
С конца XIX века для определения параллакса Солнца используют фотографические наблюдения малых планет, приближающихся к Земле на наименьшие расстояния. Среди таких планет — Эрос, иногда сближающийся с Землёй до 1/7 астрономической единицы с параллаксом, равным 60″, а также малые планеты Икар и Географ.
Следуя идеям И. Кеплера, в XVIII и XIX вв. для определения параллакса Солнца наблюдали прохождения Венеры по диску Солнца, измеряя на двух обсерваториях время, в течение которого Венера пересекает солнечный диск; теория метода разработана в 1677 Э. Галлеем.
Динамические методы определения параллакса Солнца основаны на изучении возмущений в движении планет и Луны, вызываемых притяжением других небесных тел. Параллакс Солнца p и суммарная масса Земли и Луны М, выраженная в единицах массы Солнца, связаны соотношением вытекающим из 3-го закона Кеплера. Параллакс Солнца вычисляется, если определена общая масса Земли и Луны, по возмущениям, вызываемым этими телами в движении какой либо планеты. Существуют и другие динамические методы определения параллакса Солнца.
Физические методы определения параллакса Солнца, в частности, основаны на соотношении между средней скоростью V0 движения Земли по гелиоцентрической орбите (около 29,8 км/сек) и большой полуосью а этой орбиты, то есть в конечном счёте скорость V0 можно определить: измеряя лучевые скорости звёзд, лежащих вблизи эклиптики; определяя постоянную годичной аберрации c (см. Аберрация света), равную отношению V0 к скорости света; измеряя доплеровские смещения радиолиний (с длиной волны 21 см) в спектрах межзвёздных водородных облаков. Развитие радиолокационных методов измерения расстояний между Землёй и планетами, Луной и космическими зондами, а также доплеровских смещений частот дало возможность непосредственно определить значение астрономической единицы в км. В системе астрономических постоянных, принятой в 1964, астрономическая единица равна 149,6 млн км. Таким образом, в этой системе Параллакс Солнца является производной астрономической постоянной и составляет 8,794″. При этом световая астрономическая единица (время прохождения светом расстояния, равного 1 астрономической единице) принята равной tа = 499,012 сек, а экваториальный радиус земного сфероида — равным 6378,160 км.
Источник