Как определить склонение луны

. и о видимом движении Луны

Рассмотрим теперь, как меняется склонение Луны при ее движении по небу, которое на самом деле отражает обращение Луны по орбите вокруг Земли. Плоскость лунной орбиты наклонена к эклиптике под углом 5,2°. Две точки пересечения с эклиптикой большого круга, образованного на небесной сфере этой плоскостью, называются узлами лунной орбиты. Узел, минуя который Луна попадает из южной в северную часть неба относительно эклиптики, считается восходящим, а другой — нисходящим. Вследствие вековых возмущений в движении Луны долгота узлов непрерывно меняется. Они перемещаются по эклиптике в направлении, обратном движению Луны, т. е. на запад, при этом полный оборот совершается за 18 лет и 7 мес (примерно 18,6 года).

На рис. 16, а показан случай, когда восходящий узел совпадает с точкой весеннего равноденствия Т. Тогда орбита Луны находится вне угла между эклиптикой и небесным экватором и наклонена под общим углом к экватору 5,2° + 23,5° = 28,7°. Соответственно за период оборота вокруг Земли (так называемый сидерический месяц) склонение Луны изменяется от -28,7° до +28,7°. Каждую ночь Луна восходит и заходит в разных точках горизонта в зависимости от своего склонения. Через девять с небольшим лет восходящий и нисходящий узлы меняются местами, т. е. в точке ν оказывается уже нисходящий узел (рис. 16, б). Орбита Луны в таком случае наклонена к экватору под углом 23,5° — 5,2° = 18,3°, а склонение в течение месяца меняется от -18,3° до +18,3°.

Склонением небесного тела определяются не только положения точек его восхода и захода, но и максимальная высота над горизонтом, который достигает тело в процессе суточного движения. Как уже говорилось, например, для широты Болгарии высота Солнца в день зимнего солнцестояния (δ = -23,5°) равна примерно 24°, в дни равноденствий (δ = 0) — около 47°, а в день летнего солнцестояния (δ = +23,5°) — около 71°. Существует простая формула, позволяющая вычислить эту высоту.

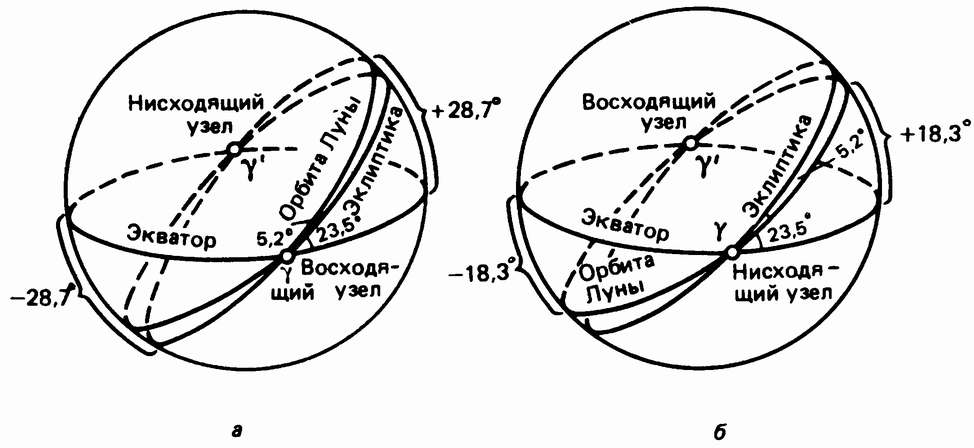
Рис. 16. Изменение склонения Луны в течение 18,6 года.

На рис. 17 показана небесная сфера, понятие о которой было введено еще древними греками. Это воображаемая сфера, на которую проецируются все небесные тела; ее центр совпадает с центром Земли, На рисунке отмечены также Северный (Р) и Южный (Р’) полюсы мира и показан небесный экватор. Земля изображена в центре как малая сфера с линиями оси вращения и экватора и произвольной точкой наблюдения А. Пересечение плоскости, перпендикулярной отвесной линии ZZ’ в месте наблюдения A, с небесной сферой образует окружность, которая называется небесным горизонтом. Географическая широта точки А — это угол φ. Легко видеть из простых геометрических соображений, что в данном месте наблюдений высота Северного полюса Р над горизонтом также равна φ, а высота экватора над горизонтом на юге составляет угол 90° — φ. На рис. 17 представлена суточная параллель, описываемая некоторым небесным телом от восхода до захода. Она, как мы знаем, параллельна экватору и находится от него на угловом расстоянии δ (склонение объекта). В момент так называемой верхней кульминации тело поднимается на наибольшую высоту над горизонтом. Обозначив ее Л, нетрудно видеть, что h = 90° — φ + δ. Географическая широта Софии φ = 42°41′ (ок. 42,5°). Предоставив читателю возможность самому вычислить полуденную высоту Солнца в столице Болгарии для четырех важных астрономических дат, займемся соответствующими вычислениями для Луны. Выше уже были указаны пределы изменений ее склонения в двух экстремальных случаях на протяжении 18,6 года.

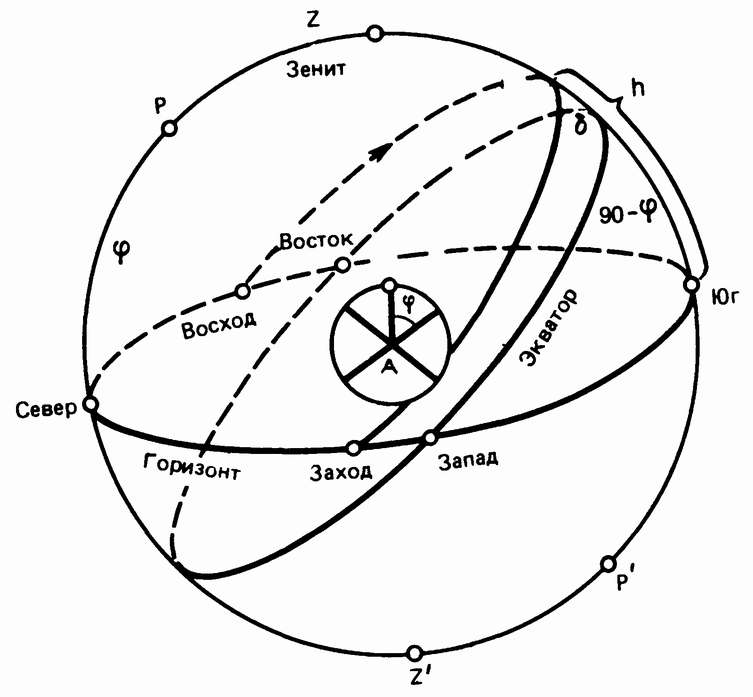
Рис. 17. Суточная параллель, описываемая звездой на небесной сфере вследствие вращения Земли вокруг своей оси.

Предположим, что сейчас лето и Солнце находится в точке летнего солнцестояния, а восходящий узел лунной орбиты в этот момент совпадает с точкой весеннего равноденствия (рис. 16, a). Пусть Луна будет в полнолунии, т. е. располагается на звездном небе в месте, прямо противоположном точке летнего солнцестояния. Очевидно, это место совпадает с точкой зимнего солнцестояния, и склонение Луны будет равно -28,7°. Легко получить, что на географической широте Болгарии высота Луны над горизонтом в верхней кульминации тогда будет около 19°. В противоположном случае, в момент зимнего солнцестояния, полная Луна, имеющая склонение + 28,7°, поднимется на высоту около 76°.

Полученный нами результат — полная Луна зимой поднимается выше, чем летом, — справедлив всегда, а не только для рассмотренного случая совпадения восходящего узла с точкой ν. Аналогично получается, что при тех же начальных условиях высота полной Луны летом для широты Ленинграда (φ примерно равна 60°) составляет всего 1,3°. Другими словами, Луна лишь слегка показывается над горизонтом и снова заходит. А в более северных широтах в полнолуние наш спутник вообще не виден!

Источник

максимального склонения Луны.

Исследование движения точек нулевого склонения Луны.

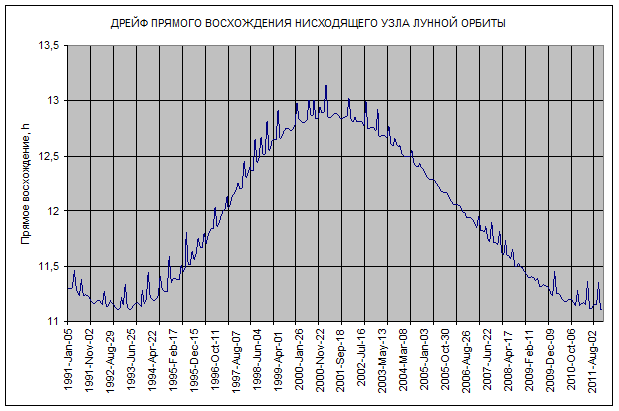
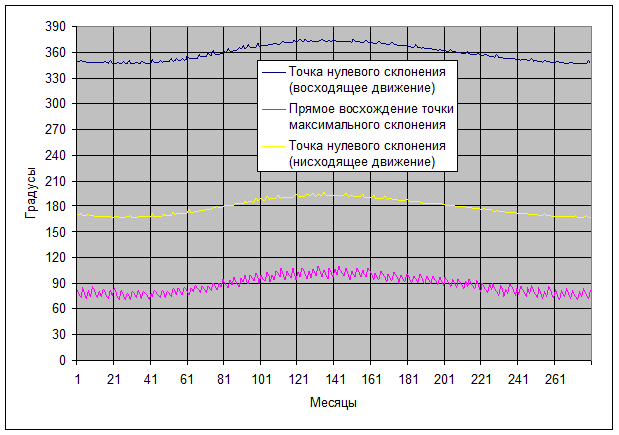
Узлами лунной орбиты принято считать точки пересечения орбиты Луны с эклиптикой. Существует, однако, и другое определение узлов: они рассматриваются как «точки, в которых орбита планеты пересекает плоскость эклиптики, а орбита Луны или искусственного спутника Земли — плоскость земного экватора». Луна пересекает плоскость земного экватора в точках, где ее склонение обращается в ноль. Анализ лунных эфемерид, взятых с сайта Лаборатории реактивного движения NASA, позволяет построить зависимость прямого восхождения точек, где склонение Луны равно нулю, от времени (Рис.1, 2).

Рис.1. Зависимость прямого восхождения точки нулевого склонения Луны от времени (нисходящее движение).

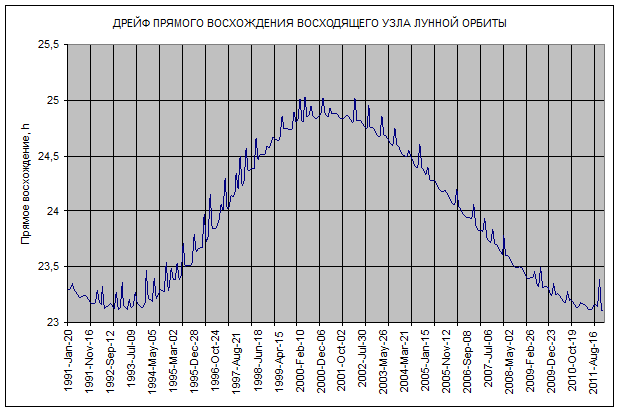
Период дрейфа точек нулевого склонения составляет 6800 суток, т.е. 18,61 года. При этом стоит отметить, что скорость дрейфа в первой половине цикла выше, чем во второй.

Рис.2. Зависимость прямого восхождения точки нулевого склонения Луны от времени (восходящее движение).

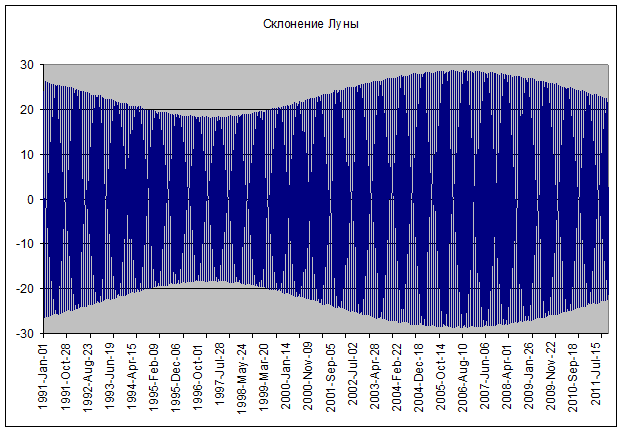
Склонение Луны связано с наклоном лунной орбиты по отношению к экваториальной плоскости. “Орбита Солнца” имеет наклон 23,43° к экваториальной плоскости Земли. Орбита Луны также имеет средний наклон 23,43° и периодическую составляющую наклона с амплитудой 5,145°(Рис. 3).

Рис. 3. Изменение склонения Луны за 21 год.

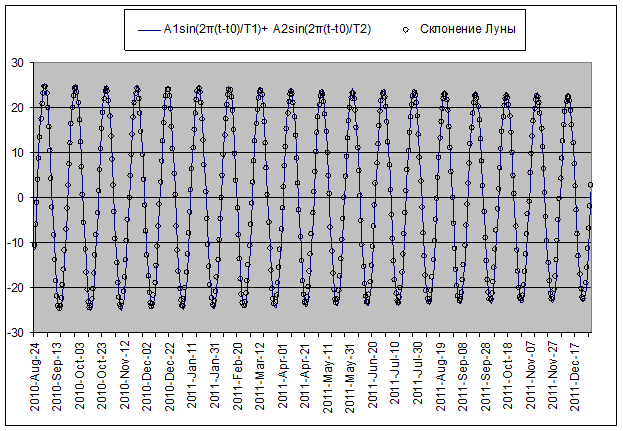
Зависимость склонения Луны от времени с достаточной точностью (Рис. 4) можно аппроксимировать функцией вида

T1=27.32166 – сидерический период Луны,

Т2=27.21222 – драконический период Луны,

t₀ = 5703.58сут — нулевая точка, начало отсчета.

Период огибающей, рассчитанный на основе значений T1 и T2, составляет 6794 дня, т.е. очень близок к 6800 сут или 18.61 года — принятому в настоящее время значению длительности цикла обращения лунных узлов по эклиптике.

Рис. 4. Аппроксимация зависимости склонения Луны от времени.

Известно, что у классического кеплеровского эллипса линия узлов орбиты должна быть перпендикулярна линии апсид. Для орбиты Луны это совсем не так. Апсиды двигаются не согласованно с узлами. Более того, апсиды могут совпадать с точками нулевого склонения Луны.

Эволюция орбиты Луны относительно небесного экватора показана на Рис. 5.

Рис. 5. Эволюции орбиты Луны относительно плоскости небесного экватора.

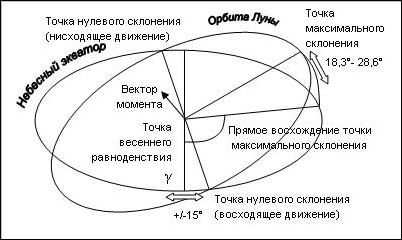
Период изменения максимального склонения Луны равен периоду движения точек пересечения орбиты Луны и эклиптики (узлов в классическом понимании). Узлы лунной орбиты в ином понимании (точки нулевого склонения) совершают дрейф +/-15° около точек весеннего и осеннего равноденствий. При этом максимальное склонение изменяется от +18,3° до +28,6°.

Взаимное расположение точек нулевого склонения и точки максимального склонения определяет направление вектора нормали к плоскости лунной орбиты. Этот вектор коллинеарен вектору орбитального момента Луны. Изменение взаимного расположения вышеназванных точек с течением времени (Рис. 6) происходит таким образом, что вектор орбитального момента описывает вокруг оси вращения Земли конус с углом при вершине около 10°.

Рис. 6. Движение точек нулевого склонения и точки

максимального склонения Луны.

Момент инерции Земли как сферы равен 9,70х10 37 кг м 2 , момент инерции Луны на орбите равен 1,09х10 40 кг м 2 . Таким образом, момент инерции Луны почти в 112 раз больше земного. Частота вращения Луны вокруг Земли, в 27.32 раза меньше частоты вращения Земли, поэтому момент импульса Луны в орбитальном движении только в 4.1 раза превышает момент импульса Земли в ее осевом вращении. Однако, по-видимому, этого достаточно, чтобы стабилизировать ось вращения Земли в том положении, в котором она пребывает, а именно 23.43° к эклиптической нормали. Механизм стабилизации, возможно, заключается во вращении вектора лунного орбитального момента около осевого момента Земли, подобно тому, как маятник с подвижной точкой подвеса (маятник Капицы) может иметь точку динамического равновесия в верхнем вертикальном положении или как велосипедист, раскачиваясь из стороны в сторону, придает устойчивое положение велосипеду даже на очень малой скорости.

Итак, анализ лунных эфемерид показал, что узлы лунной орбиты (точки нулевого склонения) «привязаны» к узлам «орбиты Солнца» — точкам весеннего и осеннего равноденствия. Вращение вектора лунного орбитального момента вокруг вектора земного осевого момента, вероятно, стабилизирует угол наклона земной оси, а может быть вызывает и саму прецессию земной оси. Если этот эффект присутствует в действительности, то несогласованное изменение параметров лунной орбиты, например в результате бомбардировки Луны крупным астероидом, может привести к изменению наклона оси вращения Земли, что неизбежно приведет к изменениям климата на планете.

Дата добавления: 2016-02-02 ; просмотров: 3223 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Видимое собственное движение Луны

Лунная орбита. Точки и линии на ней

Луна, как и все другие светила участвует в видимом суточном движении светил с востока (E) на запад (W), но даже глазомерные наблюдения показывают, что Луна имеет видимое собственное движение так как ежедневно изменяется время восхода и захода Луны, изменяется азимут (А) восхода и захода, изменяется меридиональная высота, изменяется положение Луны относительно неподвижных звёзд. Также меняется фаза Луны, всё это доказывает, что Луна имеет видимое собственное движение.

Если выбрать из Морского Астрономического Ежегодника (МАЕ) гринвичский часовой угол и склонение Луны за месяц и нанести их на небесную сферу, то получим большой круг (LL1), плоскость которого не совпадает ни с плоскостью истинного горизонта (HH1), ни с плоскостью эклиптики (BB1), а расположена к плоскости эклиптики под углом i (иота) = 5°08′.

Видимый месячный путь Луны на небесной сфере называется Лунной орбитой, и она пересекается с плоскостью эклиптики в лунных узлах.

Лунный узел, в котором склонение Луны равняется 0° и наименование меняется с южного (S) на северное (N) называется восходящим лунным узлом и обозначается знаком .

Лунный узел, в котором склонение Луны равняется 0° и наименование меняется с северного (N) на южное (S) называется нисходящим лунным узлом и обозначается знаком .

Предположим, что Земля, Солнце и Луна, одновременно кульминировали относительно какой-либо звезды, например, самой яркой звезды на небосводе, Сириуса (звезда a в созвездии Большой пёс, видимая звёздная величина – 1,4). Через сутки Солнце опоздает к моменту кульминации Земли относительно Сириуса, на 3 м 56 с или приблизительно на 4 (четыре) минуты, так как оно имеет видимое собственное годовое движение и движется со скоростью 1° в сутки. Луна опоздает к моменту кульминации Земли на 53 (пятьдесят три) минуты. Это является доказательством, что Луна имеет видимое собственное месячное движение, которое направлено в туже сторону, что и Солнце и движется относительно звезды со скоростью 13°,2 в сутки (фактически суточная скорость колеблется от 10° до 17 в сутки°), а относительно Солнца движется со скоростью 12°,2 = 49 минут в сутки.

В следствие этого момент кульминации Луны на данном меридиане каждые сутки увеличивается на 50 минут. Данная зависимость позволяет найти время кульминации Луны на любом меридиане, если известно время кульминации на каком-либо другом меридиане. Например, в Морском Астрономическом Ежегоднике (МАЕ) на каждые сутки приводится время кульминации Луны на гринвичском меридиане. Для получения момента кульминации Луны на местном меридиане необходимо проинтерполировать разность ± 50м по долготе используя формулу:

Очевидно, что на меридианах к осту (востоку) от гринвичского меридиана Луна кульминировала раньше, чем на гринвичском меридиане, а из приведённой выше формулы имеем, что на каждые 15° Восточной долготы время кульминации Луны уменьшается приблизительно на 2 минуты.

Соответственно на меридианах, лежащих к весту (западу) от гринвичского меридиана Луна кульминировала позднее, чем на гринвичском меридиане, и момент кульминации будет увеличиваться на приблизительно на 2 минуты на каждые 15° Западной долготы.

Промежуток времени, в течение которого Луна делает полный оборот по своей орбите относительно какой-либо звезды, называется сидерическим (звёздным) месяцем. Продолжительность сидерического месяца легко вычисляется. Так как один оборот равен 360°, а суточная скорость составляет 13°,2 в сутки, то продолжительность сидерического месяца равна: 360° : 13,2 °/ сут приблизительно 27,32 суток или 27д 07ч 43м 11с.

Промежуток времени, в течение которого Луна делает полный оборот по своей орбите вокруг Солнца, называется синодическим (лунным) месяцем. Продолжительность сидерического месяца легко вычисляется. Так как один оборот равен 360°, а суточная скорость составляет 12°,2 в сутки, то продолжительность сидерического месяца равна: 360° : 12,2 °/ сут приблизительно 29,53 суток или 29д 12ч 44м 03с.

Лунный месяц лежит в основе календарного месяца. В течение лунного месяца происходит весь цикл изменений вида Луны, что наблюдатель на Земле видит в виде изменения изображения диска Луны, то есть смену фаз Луны.

Двенадцать лунных месяца составляю лунный год, продолжительностью около 354 суток. Из-за разности в скорости движения с Солнцем, лунный год на 11 суток короче, чем тропический и календарный год. Вследствие этой разности дни лунного месяца, и одни и те же фазы Луны из года в год приходятся на разные даты календарного года. Они совпадут только через 19 лет. Этот 19-ти летний период называется Метоновым циклом (29,53д х 235 лунных месяцев = 6939,65д : 365,25д = 19 лет).

Склонение Луны

В течение месяца склонение Луны меняется от 0° до относительного максимума 28° 36’ S и от 0° до относительного максимума 28° 36’ N, следовательно, наибольшее изменение склонения может достигать почти 57°, при этом суточное изменение склонения колеблется от десятых долей градуса до примерно 7°.

Вследствие большой скорости изменения склонения, взятие высот Луны представляет некоторые затруднения и без навыков, как правило, наблюдатели допускают ошибки в измерениях и вычислениях.

Источник