Закон всемирного тяготения
Все тела в природе притягиваются, это свойство тел, имеющих массу. Сила, с которой тела притягиваются, называется силой гравитации (силой притяжения).
Формула закона всемирного тяготения с объяснениями
Зная массы двух тел и расстояние между ними, можно рассчитать силу их взаимного притяжения с помощью такой формулы:
\[ \large \boxed < F = G \cdot \frac
\(F \left( \text <Н>\right)\) (Ньютоны) — сила, с которой два шарообразных тела притягиваются
\( m_ <1>\left( \mbox <кг>\right) \) (килограммы) — масса первого тела
\( m_ <2>\left( \text <кг>\right) \) (килограммы) — масса второго тела
\( R \left( \text <м>\right) \) (метры) — расстояние между центрами тел
\(G \ = 6<,>67 \cdot 10^ <-11>\left( \text <Н>\cdot \frac<\text<м>^2><\text<кг>^2> \right)\) — гравитационная постоянная
- формула позволяет точно рассчитать притяжение между двумя однородными шарами;
- если тела не шарообразные, или не однородные, то силу притяжения получим с погрешностью;
- чем больше расстояние между телами, тем меньше будет погрешность;
Словесная формулировка закона всемирного тяготения
Закон всемирного тяготения словами можно сформулировать так:
Два тела притягиваются с силой
прямо пропорциональной
массам этих тел
и обратно пропорциональной
квадрату расстояния между телами.
Пояснения к закону всемирного тяготения
Сила прямо пропорциональна массам тел. Математики прямую пропорциональность записывают так:
\[ F \sim m_ <1>\cdot m_ <2>\]
Прямая пропорциональность означает: чем больше массы, тем больше сила притяжения.
Сила обратно пропорциональна расстоянию в квадрате. Математики обратную пропорциональность записывают с помощью дроби. В знаменателе этой дроби находится величина, обратно пропорциональная величине, находящейся в левой части выражения:
\[ F \sim \frac<1>
Обратная пропорциональность означает: чем больше расстояние между телами, тем меньше сила притяжения.
Что такое гравитационная постоянная
Физики часто употребляют термин: «Физический смысл». Физический смысл для чего-то – это ответ на вопрос: Что это такое с точки зрения физики?
Физический смысл гравитационной постоянной:
Гравитационная постоянная — это сила, с которой притягиваются два однородных шара, по 1-му килограмму каждый, когда они находятся на расстоянии 1-го метра один от другого.
\(G \ = 6<,>67 \cdot 10^ <-11>\left( \text <Н>\cdot \frac<\text<м>^2><\text<кг>^2> \right)\) — гравитационная постоянная
Как видно, это очень незначительная сила, поэтому в повседневной жизни мы ее не замечаем.
Куда направлена сила притяжения
Соединим прямой линией центы притягивающихся тел. Вдоль этой линии и будут направлены силы, с которыми тела притягиваются. Физики часто заменяют фразу «действие одного тела на другое» словом «взаимодействие».
\( F_ <1>\) – это сила, с которой большой шар притягивается к маленькому шарику;
\( F_ <2>\) – это сила, с которой маленький шарик притягивается к большому шару;
Из третьего закона Ньютона известно, что тела взаимодействуют с одинаковыми по модулю силами. Это значит, что \( | F_ <1>| = | F_ <2>| \). То есть, силы равны.
У физиков есть такой шуточный вопрос: «Что сильнее притягивает – Луна Землю, или Земля Луну?». Правильный ответ: «Они притягиваются с одинаковыми силами».
Как правильно выбирать расстояние для подстановки в формулу
Центр масс тела — это точка, которой мы заменяем тело для упрощения задачи.
Если тело однородное и шарообразное, то центр масс — это точка, расположенная в центре шара.
Расстояние между телами — это расстояние между центрами масс.
Рассмотрим несколько поясняющих примеров:
Пример 1. Притяжение между планетой и звездой
\( R = \left( r_ <1>+ h + r_ <2>\right) \)
Складываем радиусы шаров и расстояние между их поверхностями, получаем расстояние между центрами тел. Это расстояние и подставляем в знаменатель формулы.
Пример 2. Два шарообразных тела соприкасаются
\( R = \left( r_ <1>+ r_ <2>\right) \)
В формулу нужно подставить расстояние между центрами масс шаров. Складываем радиусы шаров и результат подставляем в формулу вместо R.
Пример 3. Малое тело покоится на поверхности планеты
\( R = r \)
Расстояние между телами — это радиус планеты. Радиус камня очень мал по сравнению с радиусом планеты, поэтому, мы радиус камня не учитываем.
Пример 4. Малое тело находится на некотором расстоянии от планеты
\( R = \left( r + h \right) \)
Складываем радиус планеты и расстояние от спутника до поверхности планеты. Полученное число является расстоянием между телами. Размеры спутника не учитываем, так как они очень малы по сравнению с радиусом планеты.
Вам будет интересно почитать:
Первая космическая скорость
Движение по окружности, центростремительная сила и центростремительное ускорение
Ускорение свободного падения
Источник
Закон всемирного тяготения в астрономии
Закон всемирного тяготения астрономия использует для множества расчетов позволяющих нам проникнуть в тайны Вселенной и углубиться в раскрытие загадок явлений, происходящих в ней. Для физики времён Ньютона этот закон стал одним из важнейших, позволяющих вместе с другими постулатами механики описывать процессы космического масштаба.
Применение закона всемирного тяготения в астрономии
Закон всемирного тяготения астрономия трактует точно так же, как и другие разделы физики, однако эта наука применяет его с более глубоким пониманием, чем просто притяжение двух объектов. Вывод Ньютона объяснил астрономам и учёным причину замкнутости орбит планет и окончательно разрушил представления о совершенных и несовершенных траекториях, царивших со времён Аристотеля, тем самым изменив вектор развития науки в сторону прогрессивных взглядов.
Благодаря догадке о всемирном притяжении люди сумели понять причину морских приливов и отливов, а также сделать предсказания на будущее о координатах расположения любой из планет Солнечной системы.
Движение Луны и земное притяжение
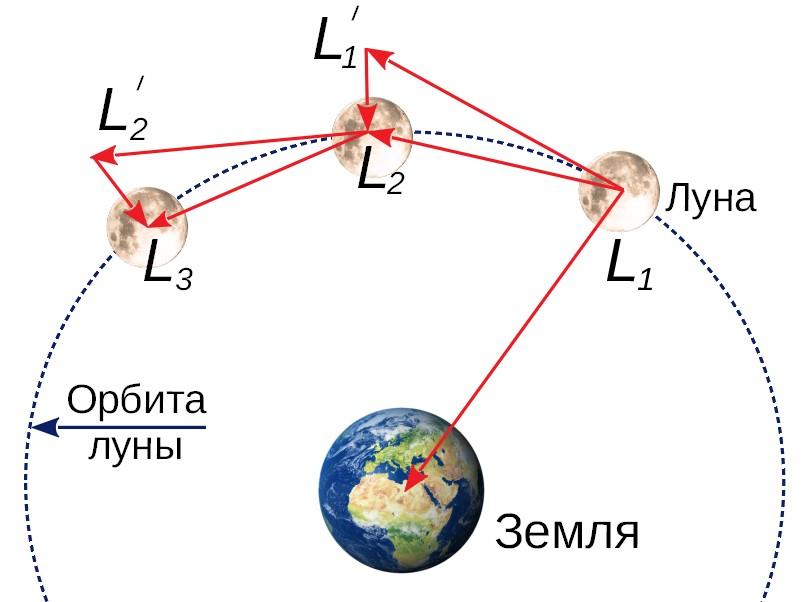
Из истории открытия закона известно, что Исаак Ньютон в своём исследовании опирался на движение Луны вокруг Земли. Связав силу тяжести, вынуждающую все незакреплённые объекты падать вниз, и неизвестную к тому моменту силу, удерживающую Луну на её орбите, учёный понял, что это одно и то же явление. Если бы притяжение не действовало на спутник, то он давным-давно свернул бы со своей наблюдаемой траектории и пролетел по касательной к ней в глубины космоса.
Такое утверждение легко доказать на схематическом рисунке, приведённом выше. Пусть – начальное положение Луны. Если бы на неё не действовала центростремительная сила, исходящая от Земли, то через некоторый промежуток времени спутник бы занял положение , однако наблюдение показывает, что небесное тело при движении приходит в точку , а после в и так далее, что доказывает наличие притяжения.
Выводом своего закона Ньютон показал зависимость земного тяготения от квадрата расстояния. Так, на поверхности нашей планеты камень обладает ускорением свободного падения м/с. Если же этот самый камень поместить на орбиту Луны, то он будет падать на Землю с ускорением м/с.
Невесомость
Чтобы ощутить притяжение Земли на себе, не нужно быть Луной, или любой из планет, или другим возможным объектом в природе. Каждый человек с самого рождения ощущает на себе силу тяжести, причём в бытовой жизни её часто называют просто весом.
Существует два интересных понятия, при которых вес может измениться – перегрузка и невесомость. Первый случай особенно знаком космонавтам и военным лётчикам, совершающим фигуры высшего пилотажа. Более приземлённые люди могут столкнуться с перегрузкой при резком торможении автомобиля, который до этого ехал с большой скоростью. Причина перегрузки — наличие ускорения при движении, которое выражается, в основном, в увеличении веса.
Если на поверхности земли принять перегрузку равной , то при старте космического корабля на человека, находящегося внутри, будет действовать сила, достигающая . То есть при взлёте космонавт может чувствовать себя в 7 раз тяжелее, чем в обычных условиях.
Невесомостью называют такое состояние, при котором вес тела равен нулю. В пределах атмосферы это возможно испытать в самолёте, движущемся с ускорением свободного падения. Это один из способов тренировки будущих астронавтов, когда самолёт набирает высоту, двигаясь строго вверх, а потом резко падает вниз. Также общеизвестный факт существования невесомости в космосе, например, на Международной космической станции. Явление отсутствия веса объясняется тем, что за пределами атмосферы при отключенных двигателях космический корабль испытывает воздействие только силы притяжения Земли. При этом и корабль, и все объекты в нём движутся с одним ускорением, а внутри челнока ощущается невесомость.
Движение небесных тел и определение их масс
Закон всемирного тяготения астрономия использует для определения траектории движения планет и других астрономических тел. Он подчиняет себе не только вращение спутников вокруг их планет, но и движение последних вокруг звёзд и так далее.
Таким образом, можно сделать немного ошеломляющий вывод о том, что всё во Вселенной в целом вращается вокруг одного центра. Вот почему постулат Ньютона называют законом всемирного тяготения.
Ещё Кеплер заметил, что планеты движутся по круговым и эллиптическим орбитам. Математически Ньютон подтвердил, что траектории также могут быть параболическими и гиперболическими. Кроме этого, уточняя кеплеровские законы (читай, вывод закона всемирного тяготения из законов Кеплера), учёный преобразовал его третий постулат, определяя, что период обращения зависит не только от геометрических характеристик орбиты, но и от массы исследуемых тел. Что позволило определять массы астрономических объектов, если известен путь друг от друга, а также период обращения.
Видео о законах Кеплера:
Один из приближённых вариантов измерения массы Земли состоит в следующем. Допустим, есть отвес, который по закону притягивается горой, при этом её масса и расстоянии до отвеса численно известны. Измеряя отклонение отвеса, можно измерить массу нашей планеты. Математически этот угол находится в зависимости от отношения масс планеты и горы, а также от отношения пути от центров Земли и горы.
Приливы и отливы
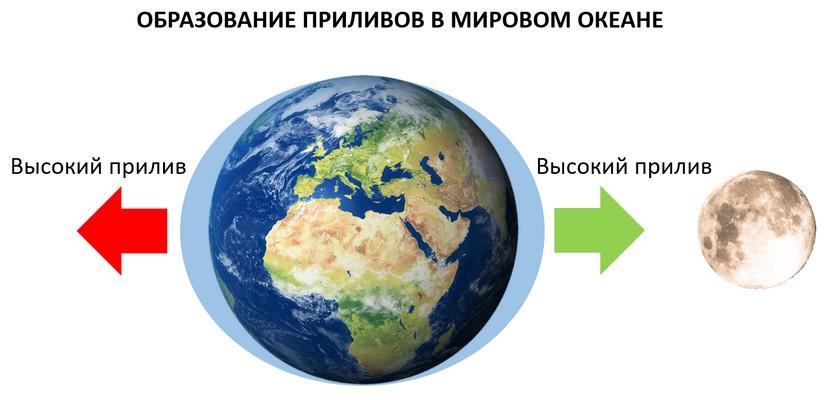
Каждый день моря и океаны затапливают берега, а затем вода отступает. Эти явления называют приливами и отливами, и происходят они с определённой периодичностью. То есть после прилива через шесть часов наступит отлив, а затем спустя такое же время – прилив, и так по кругу. Если принять оба прилива и отлива за цикл, то его продолжительность составляет двадцать четыре часа и пятьдесят минут, что соответствует промежутку времени, за который Луна занимает одну из двух кульминационных точек своей траектории. Таким образом, можно заметить зависимость между спутником Земли и движением воды, доказательство которой совершил Ньютон, тем самым показывая ещё один способ использования закона притяжения.
Исходя из третьего постулата механики, можно сказать, что не только Земля притягивает Луну, но и наоборот. При этом разные точки земного шара испытывают на себе разную по величине силу воздействия: чем ближе точка, тем сильнее притяжение. Такая разница становится причиной деформирования водной оболочки планеты: где-то она будет растянута, что вызовет прилив, а где-то сжата, и произойдёт отлив. А так как не только Луна движется вокруг Земли, но и сама Земля вращается вокруг своей оси, точки будут меняться местами между собой.
Возмущение в движении планет
Законы Кеплера, описывающие траектории движения планет, учитывают только тяготение Солнца и упускают влияние других объектов системы. Поэтому при реальных наблюдениях за вращением какого-либо небесного тела можно увидеть небольшие отклонения от предсказанной орбиты, нехарактерные для кеплеровских постулатов. Эти отклонения называют возмущениями, и в сегодняшней науке рассчитываются достаточно точно благодаря формуле тяготения и известным значениям расстояний между Солнцем и планетами, а также их масс.
Одно из самых масштабных проявлений возмущений в науке – несоответствие рассчитанного и наблюдаемого движения планеты Уран, открытой Вильямом Гершелем в 1781 году. Несмотря на то, что было учтено влияние как звезды, так и остальных тел, существовали небольшие отклонения, с которыми астрономы никак не могли примириться. Тогда было высказано предположение о существовании за Ураном ещё одной, восьмой планеты. В 1846 году на основании расчетов Урбена Леверье и Джона Адамса она была найдена, получив название Нептун. А в 1930 году подобным образом, «на кончике пера», открылось существование Плутона, споры о статусе которого не утихают и по сей день.
Характеристики тел на других планетах Солнечной системы
Взаимное притяжение тел друг к другу, а именно спутников и планет, вокруг которых они вращаются, может помочь в определении ускорения свободного падения на любой планете Солнечной системы. Важно только знать массу и радиус исследуемого объекта и подставить их в формулу:
где G – гравитационная постоянная,
M и R – масса и радиус планеты.
Для более ясного понимания, результаты проще вывести в отношении к ускорению на Земле:
| Планета | g/g зем |
|---|---|
| Меркурий | 0,38 |
| Венера | 0,9 |
| Марс | 0,38 |
| Юпитер | 2,55 |
| Сатурн | 1,12 |
| Уран | 0,97 |
| Нептун | 1,17 |
| Плутон | 0,01 |
Таким образом, масса тела, допустим, автомобиля, конечно же, не изменится, если доставить его в любую точку Вселенной. Однако простому человеку поднять его будет гораздо проще на Плутоне, чем на Земле, и совсем невозможно на Юпитере
Несмотря на дату открытия, закон всемирного тяготения астрономия активно использует и сейчас, предоставив ему статус одного из важнейших постулатов в этой научной области. Его применение позволяет объяснить множество явлений: от обычных, земных, до более глобальных, включающих в себя всю Вселенную.
Источник