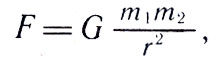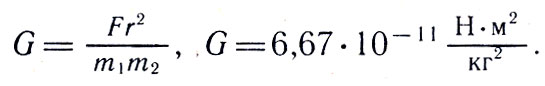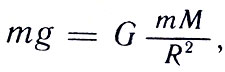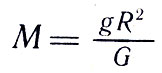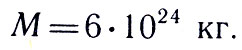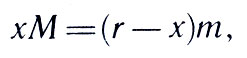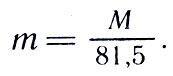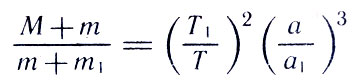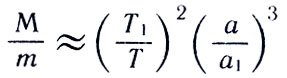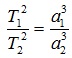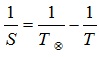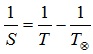Какую массу имеет солнце если за единицу взять массу луны

Масса Солнца

Солнце

Ввиду значительной удалённости от планеты Земля Солнце воспринимается человеком как тело, имеющее небольшой размер. По земным оценкам и меркам кажется, что видимый поперечник составляет 50-70 см. Если бы человек имел возможность «приземления» на Плутон, размеры светила показались бы ему другими. Итак, какова масса Солнца на самом деле – ответ на этот вопрос будет рассмотрен в статье.

О действительных размерах

Солнце – значительный по размерным показателям космический объект, который однозначно превосходит Землю в 1,3 млн раз! Значение поперечника светила нашей системы в 109 раз выше, нежели идентичный параметр у Земли, и составляет оно 1,4 млн км.

Чтобы масса Солнца была представлена более наглядно, стоит рассмотреть её в сравнительной картине. В 1 ведро можно вместить 130 тыс. пшеничных зёрен. Если в кучу будет высыпано 10 вёдер, а в сторону – положено одно маленькое зёрнышко, соотношение между этими частями будет иметь соответствие пропорциям, наблюдаемым между нашей звездой и Землёй.

Но масса Солнца с весом Земли имеет несколько другое соотношение: среднее значение плотности небесного светила вчетверо меньше, чем нашей планеты, этот показатель равняется 1,4 величины плотности воды. В свою очередь, масса Солнца превышает идентичный параметр Земли в 300 000 раз. В отношении всех планет Солнечной системы и их спутников это значение больше в 750 раз.

Весовой параметр Земли составляет, если представить точные данные, 5 958 000 000 000 000 000 000 тонн. Если выразить подобным образом вес Солнца, будет получено число, в составе которого – одна двойка и 27 нулей.

Земля и Солнце (фотомонтаж с сохранением соотношения размеров)

Известные научные сведения

Солнечная масса, или, говоря другими словами, масса Солнца, представляет собой единицу измерения массы, имеющую внесистемный тип. Она используется в астрономической науке в целях выражения звёздных весов, а также определения значений в отношении прочих астрономических объектов, к примеру, галактик, солнечных систем. Обозначение, используемое в обиходе учёных и рядовых обывателей – M. В астрономической науке его принято записывать следующим образом: M = 1,98847 * 10^30 кг.

Первый множитель не имеет максимально точного определения, поэтому может обозначаться как «плюс» или «минус» 0,00007 единиц. Массовое значение нашего естественного небесного светила, как известно, выше идентичного показателя Земли в 332 946 раз. А по точным подсчетам учёных 99,86% всей массы, относящейся к Солнечной системе, содержится именно в нашей звезде. Суммарная доля всех остальных планет имеет значение 0,0013M, причём максимальная часть приходится на Юпитер, который Солнце превышает по весу лишь в 1047,56 раз.

Физические характеристики Солнца

Формула определения

Львиная доля отдельных звёзд, присутствующих во Вселенной, имеют массовое значение от 0,08 до 50 единиц, а весовой показатель чёрных дыр и целых галактических пространств может достигать миллионов и миллиардов масс нашего главного яркого объекта. Масса Солнца, согласно формулам, разработанным в астрономической науке, может быть определена на основании формулы, которая следует из третьего закона Кеплера.

Формула расчёты солнечной массы

M = (4 * ПИ^2 * a^3) / (G * T^2),
где a – длина, которой обладает большая полуось орбитальной части планеты;
G есть величина гравитации Ньютона, которая является постоянной;
Значение T представляет собой сидерический период, в течение которого планета делает оборот вокруг нашей звезды, для Земли это значение равняется году.

Таким образом, рассматриваемый показатель играет в астрономической науке важную роль и продолжает исследоваться и изучаться.

Источник

Какую массу имеет солнце если за единицу взять массу луны

Как взвесить Солнце?

В повседневной жизни тяготение тел друг к другу (кроме силы тяжести) неощутимо. Слишком ничтожно мала гравитация (т. е. тяготение) по сравнению с другими силами. Лишь исполинские массы Земли и других космических тел создают иллюзию мощности тяготения. Но только очень тонкими экспериментами удается измерить, как притягивают друг друга небольшие тела.

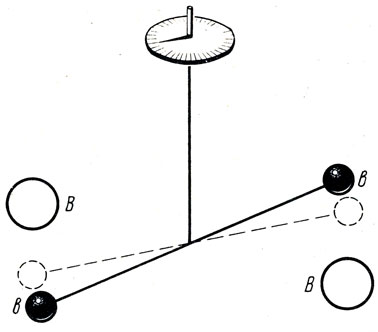
Первый успешный опыт такого рода был проделан еще в 1798 г. соотечественником Ньютона Г. Кавендишем (1731-1810). Его установка, получившая название крутильных весов (рис. 34), состояла из двух маленьких шариков (в), соединенных стержнем, который подвешивался на кварцевой нити. Вблизи этих шариков Кавендиш помещал два массивных свинцовых шара (В). Эти шары, притягивая концы стержня, закручивали кварцевую нить. По закручиванию нити можно вычислить силу притяжения F. По закону тяготения

где m₁ и m₂ — массы маленьких шариков, r — расстояние между ними и большими шарами, a G — коэффициент пропорциональности, называемый постоянной тяготения, значение которого можно определить из указанной формулы:

Рис. 34. Крутильные весы Кавендиша

Зная G и используя закон тяготения, можно определить массу Земли и других космических тел. В самом деле, пусть масса Земли М. Тогда любое тело массой т притягивается Землей с силой

где R — радиус Земли. Отсюда масса земного шара равна

Подставив в формулу известное значение величин, получим

По закону тяготения Земля и Луна обращаются вокруг общего центра тяжести С, который лежит внутри Земли. Обозначим его расстояние до центра Земли буквой х. Тогда по законам механики

где М — масса Земли, m — масса Луны, а r — расстояние между ними. Из-за движения Земли вокруг точки С меняется астрономическая долгота Солнца (по сравнению с той, которая была бы при отсутствии такого движения). Точные астрономические измерения приводят к выводу, что х = 4635 км и, следовательно,

«Взвесив» Луну, или, точнее говоря, определив ее массу, можно перейти к «взвешиванию» Солнца. Пусть некоторая планета массой т имеет спутник массой m₁. Массу Солнца обозначим М, а периоды обращения планеты вокруг Солнца и спутника вокруг планеты соответственно Т и T₁. Тогда по уточненному третьему закону Кеплера следует:

где а и a₁ — полуоси орбит планеты и спутника. Так как масса планеты мала по сравнению с массой Солнца, а у спутника много меньше, чем у планеты, приходим к приближенному равенству

Используя в качестве планеты и ее спутника Землю и Луну, получаем, что масса Солнца примерно в 333 000 раз больше массы Земли, т. е. масса Солнца приблизительно равна 2*10 30 кг.

Описанные методы «взвешивания» небесных тел не всегда применимы и далеко не единственны. Но любые иные методы в конечном счете основываются на законе всемирного тяготения: неизвестную массу тела находят по гравитационному воздействию этого тела на другие тела.

Источник

Как измерить массу Земли и массу Солнца?

Простая и надежная методика измерения массы космических тел — как узнать сколько весит Солнце, зная лишь силу притяжения между космическими телами

Как можно измерить вес (точнее, массу) Солнца, если даже реальный размер нашей “домашней звезды” настолько велик, что просто не укладывается в голове? Наверняка тут должен быть какой-то секрет… И подумав так, вы будете правы и не правы одновременно.

На первый взгляд, идея измерить массу Солнца, кажется фантастикой. На самом деле для этого не понадобится ничего, кроме простейших вычислений

С одной стороны, никакого секрета в деле измерения массы любого небесного тела сколько угодно большого размера, конечно же нет. С другой стороны, без определенных хитростей тут, конечно, не обойтись.

Давайте сразу условимся – говоря, что “нам нужно определить массу Солнца”, мы имеем ввиду “определить количество вещества входящего в состав Солнца”.

Для начала измерим массу Земли

Переформулировав задачу таким образом, мы сразу же получим зацепки ведущие к решению. Первым делом нам нужно определить величину силы притяжения возникающей между любыми двумя массами.

Принцип этого определения следующий:

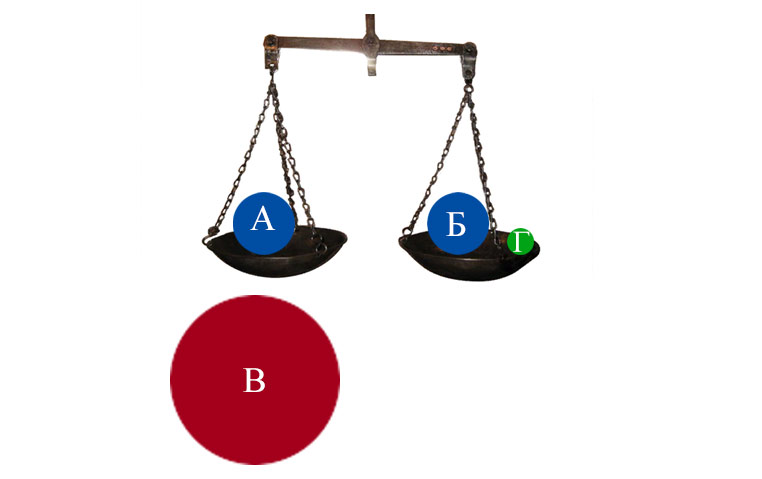
Представьте себе очень при очень чувствительные равноплечие весы с двумя чашками. В каждой чашке (А и Б) пускай лежит некий груз имеющий совершенно одинаковую массу. Весы в таком случае, будут прибывать в полном равновесии.

Теперь мы берем третье тело (В) масса которого нам также известна, и помещаем его под тело А. Взаимное притяжение между А и В, ожидаемо заставляет чашку весов А опуститься вниз. Для сохранения равновесия нам срочно необходимо добавить к массе Б очень небольшую, но опять же вполне измеримую массу Г.

Как вычислить массу планеты Земля, не выходя из дома?

Вас может заинтересовать

А вот теперь самое интересное: поскольку сила, с которой вся Земля притягивает тело Г, равна взаимному притяжению между А и В, можно без труда определить массу Земли, которая оказывается равной 6,59 х 10 21 тонн.

А теперь измерим массу Солнца!

Земля по своей орбите движется примерно так, как если бы невидимая нить соединяла ее с Солнцем. Действительно, гравитационное притяжение подобно натяжению нити, так что Земля все время движется к Солнцу, вместо того чтобы «улететь» по прямой линии, что будет, если эта “нить” вдруг оборвется. Можно сказать, что, двигаясь вокруг Солнца, Земля все время «падает» на него.

Этому “падению” соответствует отклонение ее орбиты от прямой линии, составляющее около 3 мм в секунду. Еще со времен Галилея известно, что на поверхности Земли в первую секунду своего падения всякое тело проходит 4,9 м. Расстояния 3 мм и 4,9 м прямо пропорциональны соответствующим гравитационным ускорениям, т. е. силам, действующим на единичную
массу со стороны Солнца на расстоянии Земли и Земли на ее поверхности.

Отсюда, зная, что гравитационное ускорение прямо пропорционально массе и обратно пропорционально квадрату расстояния от центра тела, можно легко вычислить, что масса Солнца в 329 390 раз больше массы Земли.

Воспользовавшись значением массы Земли, полученным выше, находим, что масса Солнца составляет 2.24 х 10 27 тонн. Полностью это немыслимое число можно записать, как 2 240 000 000 000 000 000 000 000 000 тонн.

Влияние силы тяготения на движение Земли. Путь А-С представляет собой путь пройденный Землей по орбите за 1 секунду (30 км), при этом отклонение от прямой линии B-C составит всего 3 миллиметра

Теперь уже можно вычислить и среднюю плотность Солнца, т. е. его массу, поделенную на массу воды, занимающей тот же объем.

Поскольку один кубический сантиметр воды весит один грамм, мы просто должны разделить массу Солнца (в граммах) на его объем (в кубических сантиметрах). Получим в результате число 1,42.

Иными словами, в среднем некоторый объем солнечного вещества должен весить приблизительно столько же, сколько ком битумного угля, занимающего такой же объем.

Естественно, “среднее значение” на то и среднее, чтоб представлять некую золотую середину между солнечным ядром (где плотность вещества в 10 раз превышает плотность стали) и веществом солнечной короны (где плотность падает почти до величины космического вакуума). Тем не менее, в общем и целом данная методика расчетов абсолютно верна и может с успехом применяться при расчете массы любого небесного тела – хоть астероида, хоть звезды.

Источник

ИНФОФИЗ — мой мир.

Весь мир в твоих руках — все будет так, как ты захочешь

Как сказал.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»

Тема: Законы Кеплера. Определение масс небесных тел

Цель занятия: Освоить методику решения задач, используя законы движения планет.

Теоретические сведения

При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.

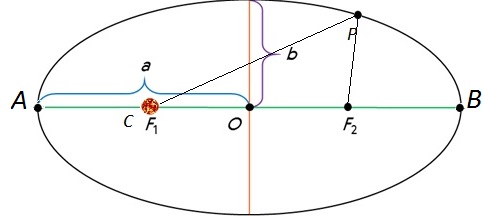
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.

Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:

Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:

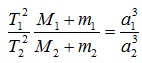
где М₁ и М₂ -массы каких-либо небесных тел, а m₁ и m₂ — соответственно массы их спутников.

Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:

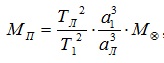
где Т_л и α _л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.

Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,

а) для внешней планеты формула имеет вид:

б) для внутренней планеты:

Выполнение работы

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.

Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.

Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.

Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?

Примеры решения задач 1-4

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Источник