Задачи по теме: «Момент инерции. Закон сохранения момента инерции и момента импульса»
Задачи по теме: «Момент инерции. Закон сохранения момента инерции и момента импульса».
1. На барабан радиусом R=0,5 м и с горизонтальной осью вращения намотан шнур, к концу которого привязан груз массой m = 10 кг. Найдите момент инерции барабана, если известно, что его угловое ускорение равно 
. Тернием пренебречь.
m = 10 кг 
Вращение барабана происходит под
действием силы F. Из второго закона Ньютона
= ∆ω/∆t = ∆υ/R∆t = a/R → a = εR
M = Jε – момент силы через момент инерции для вращающегося тела.
M = Fd = FR – момент силы вращающей барабан.
По закону сохранения момента сил
J = (m ( g – εR) R)/ ε = 22,5 (кг м²)
2. К ободу однородного диска радиусом R=0,2м массой m=1,2 кг приложена постоянная сила 100 Н, при вращении на диск действует момент силы трения, равный 5 нм. Чему равно угловое ускорение диска?
R = 0, 2 м Из оснавного управления динамики вращательного
m = 1, 2 кг движения M=Jε
F = 100 Н Сила действующая на обод F`= F — Fтр. Из M = 5 нм момента силы трения Fтр = M\R = 25 Н
ε = ? Момент силы F`- M=F`R по закону сохранения
J = mR² –момент инерции обруча
3. Шарик, диаметр которого равен 6 см, катится по полу и останавливается через t = 2с, пройдя расстояние S = 70 см. Определите коэффициент трения качения, считая его постоянным.
d = 0, 06 м М=εJ — основное уравнение вращательного движения.
t = 2c J= 0,4mr2 — момент инерции шара.
S= 0,7м. 
M= 0,4 m r2 a/ r= 0,4 a m r
Момент силы трения M = Fтр r
По закону сохранения момента сил
S= at2/2 
a=2S/t2 = 1,4/4 = 0,35 м/с2
4. Во сколько раз уменьшится угловая скорость вращения человека, если момент инерции изменится от 1 кг м² до 1,25 кг м²?
L1 = J1ω1 — момент импульса в первом состоянии.
L2 = J2ω2 — момент импульса во втором состоянии.
L1 = L2 — закон сохранения момента импульса.
Ответ: 
5. Найти момент импульса Земного шара М3 = 6·1024 кг, R3 = 6,4·10³ км, если точки поверхности Земли вращаются со скоростью 36 км/ ч.
M3 = 6·1024 кг L = Jω J= 0,4 M3R3²- момент инерции шара.
R3 = 6,4·10 6 м ω = υ/ R
υ = 10 м\с L = 0,4 M3 υ R3= 15,36·10³º кг м²/с.
Ответ: L = 15, 36·10³º кг м²/с
6. Комета Галлея движется вокруг солнца по вытянутому эллипсу. Наибольшее удаление от солнца равно 35,2 а. е., а наименьшее удаление — 0,6 а. е.. Найти отношение максимальной скорости кометы к минимальной.
R1 = 35, 2 а. е. 
момент импульса при наибольшем
R2 = 0, 6 а. е. удалении.
момент инерции кометы при наибольшем
момент импульса кометы при
L1 = L2 – закон сохранения момента импульса.
Ответ: 
7. Человек стоит на вращающейся с некоторой угловой скоростью платформе. В вытянутых в сторону руках он держит по гире, массой каждой из них m = 5 кг. Расстояние от гирь до оси вращения R1=0,71м. Во сколько раз изменится частота вращения человека, если он прижмет к себе руки так, что расстояние от оси вращения до гири станет R2= 0,2 м. Момент инерции человека считайте в обоих случаях равным J0 = 1 кг м.²
m = 5 кг Момент импульса в первом случае
R1=0,71м 
R2= 0,2 м 
момент инерции в первом случае.
J0 = 1 кг м² 
момент инерции во втором случае.
закон сохранения момента импульса.
Ответ: 
8. Человек массой m1 = 60 кг находится на неподвижной круглой платформе радиусом R2= 10м и массой m2 = 120 кг, которая может вращаться вокруг своей вертикальной оси. С какой угловой скоростью будет вращаться платформа, если человек станет двигаться по окружности радиусом R1= 5м с линейной скоростью υ1= 2 м/с относительно платформы.
m1 = 60 кг момент импульса человека;
R2= 10м 
момент инерции человека.
m2 = 120 кг 
R1= 5м 
υ1= 2 м/с 
момент импульса платформы
закон сохранения импульса.
9. Считая Солнце однородным шаром, оцените минимальный радиус и период вращения вокруг своей оси пульсара, который мог бы образоваться после сжатия Солнца под действием силы тяготения при исчерпании внутренних источников энергии, поддерживающих высокую температуру газа. Радиус Солнца Rc = 7·108 м, период вращения вокруг оси Тс = 2,2·106 с. Масса Солнца Мс = 2·10³º кг.
Rc = 7·108 м Момент импульса Солнца
Тс = 2,2·106 с 
Мс = 2·10³º кг 
момент инерции Солнца
Rп = ? Тп = ? 
Момент импульса образовавшегося пульсара
По закону сохранения импульса
Вращение пульсара происходит под действием силы тяготения.
Для удобства расчета (*) возведем в квадрат
Ответ: Rп =
Источник
§ 117. Законы движения планет
В конце XVI в. датский астроном И. Кеплер, изучая движение планет, открыл три закона их движения. На основании этих законов И. Ньютон вывел формулу для закона всемирного тяготения. В дальнейшем, используя законы механики, И. Ньютон решил задачу двух тел — вывел законы, по которым одно тело движется в поле тяготения другого тела. Он получил три обобщенных закона Кеплера.
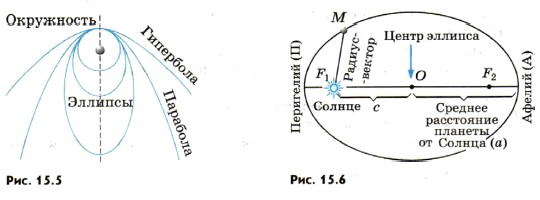
Первый закон Кеплера. Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе (рис. 15.5).
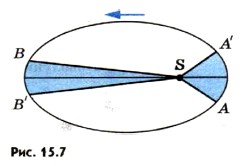
Планеты движутся вокруг Солнца по эллиптической орбите (рис. 15.6). Ближайшая к Солнцу точка орбиты называется перигелием, самая далекая — афелием. Линия, соединяющая какую-либо точку эллипса с фокусом, называется радиус-вектором. Отношение расстояния между фокусами к большой оси (к наибольшему диаметру) называется эксцентриситетом е. Эллипс тем сильнее вытянут, чем больше его эксцентриситет. Большая полуось эллипса а — среднее расстояние планеты до Солнца.
По эллиптическим орбитам движутся и кометы и астероиды. У окружности е = 0, у эллипса 0 1 (см. рис. 15.5).
Движение естественных и искусственных спутников вокруг планет, движение одной звезды вокруг другой в двойной системе также подчиняются этому первому обобщенному закону Кеплера.
Второй закон Кеплера. Каждая планета движется так, что радиус-вектор планеты за равные промежутки времени описывает равные площади.
Планета проходит путь от точки А до А’ и от В до В’ (рис. 15.7) за одно и то же время. Другими словами, планета движется быстрее всего в перигелии, а медленнее всего — когда находится на наибольшем удалении (в афелии). Таким образом, второй закон Кеплера определяет скорость движения планеты. Она тем больше, чем планета ближе к Солнцу. Так, скорость кометы Галлея в перигелии равна 55 км/с, а в афелии 0,9 км/с.
Третий закон Кеплера. Куб большой полуоси орбиты тела, деленный на квадрат периода его обращения и на сумму масс тел, есть величина постоянная.
Если Т — период обращения одного тела вокруг другого тела на среднем расстоянии а, то третий обобщенный закон Кеплера записывается как
где М1 и М2 — массы притягивающихся двух тел, a G — гравитационная постоянная. Для Солнечной системы масса Солнца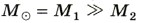 
массы любой планеты, и тогда
Правая часть уравнения — постоянная для всех тел Солнечной системы, что и утверждает третий закон Кеплера, полученный ученым из наблюдений.
Третий обобщенный закон Кеплера позволяет определять массы планет по движению их спутников, а массы двойных звезд — по элементам их орбит.
Движение планет и других небесных тел вокруг Солнца под действием силы тяготения происходит по трем законам Кеплера. Эти законы позволяют рассчитывать положения планет и определять их массы по движению спутников вокруг них.
Вопросы к параграфу
1. Перечислите основные элементы эллиптической орбиты планеты.
2. Как связаны периоды обращения планет с их средними расстояниями до Солнца?
3. Сформулируйте первый обобщенный закон Кеплера.
4. Запишите третий обобщенный закон Кеплера.
Источник
Комета Галлея: с глубокой древности до наших дней. Часть_1
Знаменитая комета движется вокруг Солнца по вытянутой эллиптической орбите, дальняя точка которой находится за орбитой Нептуна, а ближняя расположена внутри орбиты Венеры. Период обращения небесного тела равен 76 годам.
Человечество наблюдает приближения кометы с глубокой древности. Первые записи о появлении косматой звезды на небе датируются 240 г. до н. э.
Эдмунд Галлей первым предположил, что кометы 1531, 1607 и 1682 годов — один и тот же объект, и это было блестящей догадкой, поскольку в те времена астрономы понимали законы движения небесных тел не так хорошо, как сейчас, а кометы и вовсе представлялись загадочным и малопонятным явлением.
Также Галлей предсказал возвращение космического объекта и определил приблизительную дату события — 1758 год. Впоследствии комету назвали в честь этого выдающегося ученого.
Поначалу в предсказание Галлея поверили не все. Многое в поведении небесных тел тогда еще оставалось неисследованным и вызывало споры.
Наука стремительно развивалась. Уже в 1687 году увидел свет знаменитый труд Ньютона «Математические начала натуральной философии», не без участия того же Эдмунда Галлея, между прочим.
Трактат совершил революцию в физике. Непонятные и загадочные природные процессы и явления стали объяснимыми и предсказуемыми.
В «математических началах» Ньютон сформулировал закон всемирного тяготения и три закона классической механики. Наука о движении небесных тел – небесная механика — вышла на качественно новый уровень развития.
Перенесемся еще на семьдесят лет вперед. В 1758 году учение Ньютона приняли в научных кругах почти повсеместно. Наиболее дальновидные люди не сомневались и в предсказании Галлея.
Нашлись и такие, кто вызвался определить более или менее точную дату приближения знаменитой кометы к Солнцу. Это были французские ученые Клеро, Лаланд и Николь-Рейн Лепот – жена известного в Париже механика и часовщика, но в первую очередь талантливый и неутомимый математик.
На долю мадам Лепот выпала значительная часть вычислений, в которых надо было учитывать гравитационное влияние Юпитера и Сатурна. В середине XVIII века решение подобной научной задачи было сродни подвигу, поскольку производительных вычислительных машин тогда еще не существовало. С этой задачей ученые блестяще справились.
15 ноября 1758 года состоялось очередное заседание Парижской академии наук, на котором сообщество ученых узнало дату прохождения кометой перигелия – самой близкой к Солнцу точки орбиты. Клеро, Лаланд и мадам Лепот определили, что это событие должно было произойти 13 апреля 1759 года с возможной погрешностью 30 дней, на год позже предсказания Галлея.
Астрономы принялись за поиски, ведь небесная гостья должна была появиться на небосводе в ближайшее время. Удача, как это нередко бывает, улыбнулась малоизвестному, хоть и не чуждому науке человеку — немецкому астроному-самоучке Иоганну-Георгу Паличу.
Настойчивый наблюдатель обнаружил комету в ночь под Рождество 25 декабря 1758 года. Через перигелий небесная странница прошла 13 марта 1759 года – на 31 день раньше, чем предсказали Клеро, Лаланд и Лепот.
Дальнейшее изучение кометы Галлея отражает развитие науки и совершенствование методов научных исследований. С течением времени в распоряжении ученых появлялись все более сложные и эффективные способы получения информации о небесных объектах.
В 1910 году астрономы впервые сфотографировали комету Галлея. В тот год путь небесного тела располагался так близко к Земле, что наша планета должна было пройти через ее хвост. Это обстоятельство вызвало интерес ученых и беспокойство среди обывателей.
Опасения не подтвердились. Пробы воздуха и измерения свечения атмосферы не показали никаких аномалий. Дело в том, что хвосты комет имеют очень низкую плотность и не могут оказать какого-либо заметного влияния на процессы, которые происходят на Земле.
В последний раз комета Галлея приблизилась к Земле в 1986 году. Условия видимости небесного тела в тот период были наихудшими за последние 2000 лет, но астрономов-профессионалов это вряд ли могло огорчить, ведь в их распоряжении уже были методы исследований, связанные с использованием межпланетных космических аппаратов.
Ученые всего мира объединили усилия для изучения самой знаменитой кометы. К космическому объекту отправились несколько миссий: советские «Вега-1» и «Вега-2», европейская «Джотто» и две небольшие японские станции «Суисей» и «Сакигаке». Об этом мы расскажем в одной из наших следующих публикаций.
Здесь вы можете почитать еще что-нибудь интересное, пока мы готовим для вас очередной материал.
Ставьте «Like», оставляйте свои комментарии и подписывайтесь на наш канал «Галактика» , если вам понравилась наша статья.
Источник