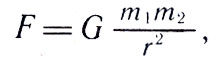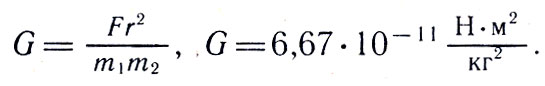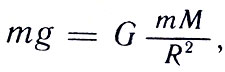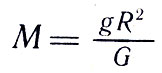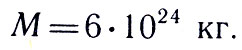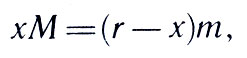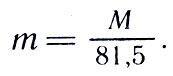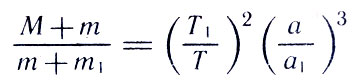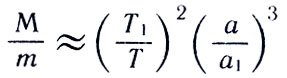Кто определил массу солнца

Как взвесить Солнце?

В повседневной жизни тяготение тел друг к другу (кроме силы тяжести) неощутимо. Слишком ничтожно мала гравитация (т. е. тяготение) по сравнению с другими силами. Лишь исполинские массы Земли и других космических тел создают иллюзию мощности тяготения. Но только очень тонкими экспериментами удается измерить, как притягивают друг друга небольшие тела.

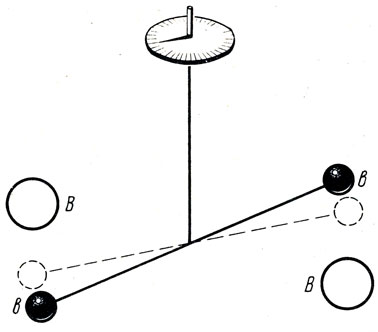
Первый успешный опыт такого рода был проделан еще в 1798 г. соотечественником Ньютона Г. Кавендишем (1731-1810). Его установка, получившая название крутильных весов (рис. 34), состояла из двух маленьких шариков (в), соединенных стержнем, который подвешивался на кварцевой нити. Вблизи этих шариков Кавендиш помещал два массивных свинцовых шара (В). Эти шары, притягивая концы стержня, закручивали кварцевую нить. По закручиванию нити можно вычислить силу притяжения F. По закону тяготения

где m₁ и m₂ — массы маленьких шариков, r — расстояние между ними и большими шарами, a G — коэффициент пропорциональности, называемый постоянной тяготения, значение которого можно определить из указанной формулы:

Рис. 34. Крутильные весы Кавендиша

Зная G и используя закон тяготения, можно определить массу Земли и других космических тел. В самом деле, пусть масса Земли М. Тогда любое тело массой т притягивается Землей с силой

где R — радиус Земли. Отсюда масса земного шара равна

Подставив в формулу известное значение величин, получим

По закону тяготения Земля и Луна обращаются вокруг общего центра тяжести С, который лежит внутри Земли. Обозначим его расстояние до центра Земли буквой х. Тогда по законам механики

где М — масса Земли, m — масса Луны, а r — расстояние между ними. Из-за движения Земли вокруг точки С меняется астрономическая долгота Солнца (по сравнению с той, которая была бы при отсутствии такого движения). Точные астрономические измерения приводят к выводу, что х = 4635 км и, следовательно,

«Взвесив» Луну, или, точнее говоря, определив ее массу, можно перейти к «взвешиванию» Солнца. Пусть некоторая планета массой т имеет спутник массой m₁. Массу Солнца обозначим М, а периоды обращения планеты вокруг Солнца и спутника вокруг планеты соответственно Т и T₁. Тогда по уточненному третьему закону Кеплера следует:

где а и a₁ — полуоси орбит планеты и спутника. Так как масса планеты мала по сравнению с массой Солнца, а у спутника много меньше, чем у планеты, приходим к приближенному равенству

Используя в качестве планеты и ее спутника Землю и Луну, получаем, что масса Солнца примерно в 333 000 раз больше массы Земли, т. е. масса Солнца приблизительно равна 2*10 30 кг.

Описанные методы «взвешивания» небесных тел не всегда применимы и далеко не единственны. Но любые иные методы в конечном счете основываются на законе всемирного тяготения: неизвестную массу тела находят по гравитационному воздействию этого тела на другие тела.

Источник

Как ученые посчитали массу Солнца?

На любое тело действуют две силы или две «скорости» — сила тяготения (маленький объект падает на большой) и, собственно, скорость, с которой этот объект летит «прямо».

Первая картинка из гугла с какой-то там задачи вполне подходит для пояснения.

Если скорость большая — то тело совершает дугу и улетает. Как делают кометы.

То есть, вот она летела-летела, начала притягиваться, но поскольку летела слишком быстро, не успела упасть, а сделала дугу и улетела дальше.

Если сила тяготения большая — то тело просто падает.

А вот если оно летает по кругу — значит, эти две силы равны между собой. Земля пытается улететь, но её по чуть-чуть притягивает к себе Солнце, постоянно изменяя её траекторию вплоть до замкнутого состояния.

Центростремительная сила вычисляется по формуле F=ma. Где массу Земли мы знаем (вычислили по ходу развития науки), а ускорение — вычисляется из того, что Земля делает один оборот за год.

И, как я уже объяснил выше, эта сила должна быть равна силе тяготения. Ну а тяготение рассчитывается исходя из массы двух тел. И зная массу Земли, расстояние до Солнца, и силу, которая на Землю действует, мы спокойно можем вычислить массу Солнца.

Для расчёта в наше время хватает буквально школьного уровня знаний.

По примерно такой же методике вычисляется и масса любых других объектов — спутников, вращающихся вокруг планеты, других планет, вращающихся вокруг звёзд, самих звёзд, взаимодействующих друг с другом и так далее.

Источник

Как ученые измерили массу Земли и других планет?

Планета – объект большой, его на весы не поставишь. Как же ученым удалось узнать массу Земли? Как измеряется масса далеких космических объектов?

Занимательная физика

Существует 2 способа определения массы Земли: с помощью барометра и математических вычислений, или анализа частиц нейтрино.

Барометр и законы Ньютона

Метод, применяемый с XVIII века. Для расчета используются второй закон Ньютона (F=mg) и закон всемирного тяготения (F=G*m*M/R^2).

F – это сила земного притяжения барометра, G – коэффициент гравитационной постоянной, R – радиус планеты, m – вес прибора, M – вес планеты.

Отдельно масса Земли вычисляется по формуле: M = g*R^2/G, где g – это ускорение свободного падения.

Ускорение свободного падения узнали, сбросив барометр с высокой башни и измерив время, которое он пролетел до столкновения с землей. Выяснилось, что за каждую последующую секунду барометр преодолевал почти 9.8 метров. Таким образом, g = 9.8 м/с².

Радиус Земли был известен еще с Античности. Столь сенсационное открытие сделал греческий математик Эратосфен в III веке до н.э.

Ученый подождал день летнего солнцестояния. В это время светило находится в самой высокой точке на небе и в 12 часов отбрасывает наименьшую тень в году.

Математик присмотрелся к обелиску, стоящему неподалеку, измерил отбрасываемую им тень, измерил сам обелиск, высчитал все углы, а потом сделал то же самое в соседнем городе. Расчеты дали ему окружность земли в 38.5 тысяч километров. Современные ученые пересчитали окружность подобным методом и высчитали 40 000 км.

Планета идеальным шаром не является, а потому ее радиус оказался 6371 км.

Труднее всего было найти коэффициент гравитационной постоянной. Для этого исследователи взяли однотонный свинцовый шар и посмотрели, с какой силой он притягивал барометр.

G = 6,67430(15)*10ˆ(-11) Н·м²·кг²

Подставив все эти цифры в уравнение, ученые высчитали, что Земля весит шесть септиллионов кг или 6^24 кг .

Это мельчайшие субатомные частицы, которые испускает Солнце. Они проходят планету насквозь.

Источник

Гений, которому удалось взвесить Солнце

Он доказал, что всякие два тела — от мельчайших частиц до величайших солнц — притягивают друг друга со строго определенной силой, величину которой он научил нас вычислять. Это «всемирное тяготение» тождественное всем знакомой земной тяжестью. Он объяснил, исходя из открытого им закона всемирного притяжения, приливы и отливы в океанах. Он определил массы солнца и планет, а также вычислил силу тяжести на их поверхности.

Он указал причину третьего движения земного шара; движение это выражается в том, что продолжение земной оси описывает среди звезд круг в течение 26 тысяч лет, и роль Полярной звезды с течением веков переходит от одной звезды к другой. До Ньютона движение комет, их появление представлялось совершенно загадочным. Ньютон доказал, что кометы, подобно планетам, обращаются вокруг солнца, подчиняясь закону тяготения.

Он изобрел телескоп с зеркалом (отражательный), весьма удобный и очень сильный. Небольшая 15-сантиметровая зрительная трубка Ньютона была так же сильна, как существовавшие до этого времени полутораметровые трубы иной конструкции. Он доказал целым рядом убедительных опытов, что свет, который мы считаем белым, может быть разложен на отдельные цвета — фиолетовый, синий, голубой, зеленый, желтый и т. д. Он подробно исследовал способ распространил звука.

Он первый установил, что тела плавятся и кипят при постоянной температуре. Он открыл закон охлаждения тел. Он создал ту математическую науку, которая теперь называется «дифференциальным исчислением» и является одной из главнейших отраслей высшей математики. Углубленное изучение природы и овладение се силами стало возможно лишь благодаря этому могучему математическому орудию. Каждой из этих заслуг в отдельности было бы достаточно, чтобы заслужить почетное имя в истории науки. С датами рождения и смерти Ньютона связаны следующие две хронологические загадки:

1) Мы празднуем рождение Ньютона 5 января 1643 г., а между тем на его могильном памятнике имеется надпись: «Родился 25 декабря 1642 г.» Кроме того, все биографы отмечают, что Ньютон родился в год смерти Галилея; великий же итальянский физик умер 8 января 1642 года. Почему же мы теперь переносим дату рождения на следующий год?

2) Двухсотлетие смерти Ньютона отмечалось всем миром в апреле 1928 г., а надпись на могильной плите гласит, что он умер 20 марта 1727 г. Отчего такое расхождение?

Разгадки очень просты. Причина первого несоответствия — в различии календарных стилей! Мы ведем счет по так называемому Грегорианскому календарю, а в эпоху Ньютона Англия жила еще по Юлианскому календарю. На родине же Галилея — в Италии — новый календарный счет был введен еще в конце XVI века, до смерти великого ученого. Причина второй неувязки сложнее. Англия приняла обычай начинать год 1 января только в середине XVIII века, после смерти Ньютона. До того англичане начинали год 25 марта. Поэтому современники Ньютона относили дату его смерти (20 марта) к 1728 г., мы же относим ее к 1729 г. Сюда присоединяется еще разница календарных стилей.

В свободные от школьных занятий часы будущий основатель теоретической механики всегда что-нибудь мастерил. Наблюдая за постройкой ветряной мельницы, юный Ньютон так хорошо познакомился с ее устройством, что смог самостоятельно изготовить ее модель. Вертясь на крыше дома, она вызывала всеобщее удивление. Вскоре Ньютон изменил устройство своей мельницы так, что ее приводила в движение сила живого двигателя, — мышь, которую мальчик-изобретатель называл «мельником».

Стараясь схватить подвешенный кусочек мяса, четвероногий мельник невольно вертел колесо. В школе, где учился Ньютон, никто не умел так искусно изготовлять и запускать бумажные змеи, как он. Будущий исследователь с помощью законов сопротивления воздуха придавал своим змеям самые разнообразные формы, желая установить, при какой форме змей всего лучше запускается. В темные зимние утра он иногда привязывал к змею зажженный фонарь и запускал его ввысь. Окрестное население удивленно и не без страха смотрело на эту искусственную комету, не подозревая, кто виновник ее внезапного появления. Впоследствии Ньютон занялся и настоящими кометами. До Ньютона эти капризные светила не подчинялись как будто никаким законам. Ньютон первый определил движение комет и нашел его законы.

Когда в 1680 г. появилась на небе огромная комета, занимавшая своим хвостом почти четверть неба, он вычислил ее путь и доказал, что она, как и планеты, огибает солнце, но только движется по сильно вытянутой кривой. А когда через два года появилась другая большая комета (открытая другом Ньютона — Галлеем), то оба ученых с такой точностью установили ее обращение, что стало возможно даже предсказать, в каком году она снова приблизится к солнцу. Закон всемирного тяготения Ньютон открыл на двадцать третьем году жизни, когда, покинув из-за чумной эпидемии университетский город, он отдыхал в родной деревне.

Существует рассказ о том, что на мысль о всемирном тяготении навело Ньютона яблоко, упавшее к его ногам с дерева. Дерево это долго еще после смерти Ньютона показывали в его саду, пока оно не было повалено бурей. Однако этот рассказ совершенно легендарен. Когда Ньютона спрашивали, как сделал он свои открытия, он отвечал: «Я постоянно думал о них. Я беспрестанно размышляю о предмете моих исследований и терпеливо жду, когда слабый проблеск постепенно превратится в полный свет». Не случайное падение яблока, а изумительная настойчивость мысли приводят к открытиям. Справедливо сказано, что гениальность есть не что иное, как «терпение мысли».

Источник

Солнечная масса

Со́лнечная ма́сса, или ма́сса Со́лнца — внесистемная единица измерения массы, применяющаяся в астрономии для выражения массы звёзд и других астрономических объектов (например, галактик). Она обозначается через и равна массе Солнца:

= (1,98892 ± 0,00025)·10 30 кг. [1]

Солнечная масса приблизительно в 333 000 раз превышает массу Земли. Около 99,86 % массы Солнечной системы содержится в Солнце; общая масса всех планет составляет лишь около 0,0013 , причём бо́льшая часть суммарной массы планет содержится в Юпитере (его масса в 1047,56 раз меньше массы Солнца) [1] . Большинство отдельных звёзд во Вселенной имеют массу от 0,08 до 50 , но масса чёрных дыр и целых галактик может достигать миллионов и миллиардов солнечных масс.

Солнечная масса может быть рассчитана [2] по формуле [3] , следующей из третьего закона Кеплера:

где T — сидерический период обращения планеты вокруг Солнца (для Земли T = 1 сидерическому году ),

См. также

Примечания

↑ 12 К. У. Аллен. Астрофизические величины. М .: Мир, 1977. — 279 с.
↑ Harwit, Martin (1998), «Astrophysical concepts» (3 ed.), Astronomy and astrophysics library, Springer, сс. 72, 75, ISBN 0-387-94943-7 ,
↑ Эта формула применима для случая орбиты, близкой к круговой, малости массы планеты и в пренебрежении релятивистскими эффектами.

Wikimedia Foundation . 2010 .

Смотреть что такое «Солнечная масса» в других словарях:

Масса Солнца — В астрономии солнечной массой называют единицу измерения массы для выражения массы звёзд и прочих огромных объектов (например, галактик). Она равна массе Солнца: Солнечная масса в 333000 раз превышает массу Земли. Более 99 % массы Солнечной… … Википедия

Солнечная светимость — Солнечная светимость, единица светимости (то есть количества энергии, выделяемой в единицу времени), обычно используемая астрономами для представления светимости звёзд. Равна светимости Солнца, составляющей 3,827·1026 Вт или 3,827·1033… … Википедия

Солнечная система — в представлении художника. Масштабы расстояний от Солнца не соблюдены. Общие характеристики Возраст … Википедия

Солнечная система как гравитационный атом Бора — представление Солнечной планетной системы в виде модели гравитационного атома Бора с радиусом произвольной орбиты в общем виде: где м радиус первой орбиты (не обязательно заполненной) планет земной группы (n = 3,4,5,6,8), и м радиус первой орбиты … Википедия

СОЛНЕЧНАЯ СИСТЕМА — состоит из Солнца, планет и спутников, множества астероидов и их осколков, комет и межпланетнойсреды. С. с. расположена вблизи центральной плоскости Галактики нарасстоянии ок. 8 кпк от её центра. Линейная скорость вращения С. с. вокруггалактич.… … Физическая энциклопедия

СОЛНЕЧНАЯ СИСТЕМА — Солнце и обращающиеся вокруг него небесные тела 9 планет, более 63 спутников, четыре системы колец у планет гигантов, десятки тысяч астероидов, несметное количество метеороидов размером от валунов до пылинок, а также миллионы комет. В… … Энциклопедия Кольера

Солнечная система — состоит из Солнца, 9 планет, обращающихся вокруг него, их спутников, малых планет (астероидов) и их осколков, комет и межпланетной среды. Внешней границей Солнечной системы принято считать сферу гравитационного влияния Солнца радиусом около… … Энциклопедический словарь

Солнечная радиация — Все процессы на поверхности земного шара, каковы бы они ни были, имеют своим источником солнечную энергию. Изучаются ли процессы чисто механические, процессы химические в воздухе, воде, почве, процессы ли физиологические или какие бы то ни было… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Масса Юпитера — Юпитер Улучшенное изображение Юпитера на базе снимков Вояджера 1 Орбитальные характеристики Афелий 816 520 800 км (5.458104 а.е.) … Википедия

Солнечная батарея — батарея солнечных элементов, полупроводниковый Фотоэлектрический генератор, непосредственно преобразующий энергию солнечной радиации в электрическую. Действие солнечных элементов (СЭ) основано на использовании явления внутреннего… … Большая советская энциклопедия

Источник