Квадратурная амплитудная модуляция созвездие

Квадратурная модуляция (QAM)

Для увеличения скорости передачи данных используют так называемую квадратурную амплитудную модуляцию QAM, которая является амплитудно-фазовым видом модуляции. QAM применяется в кабельных модемах, в стандарте цифрового телевидения DVB-C, а также, в цифровом радиовещании СВЧ диапазона.

С точки зрения скорости передачи этот вид модуляции намного более эффективен по сравнению с двоичной (BPSK), четырехпозиционной (QPSK) или восьмипозиционной (8-PSK) фазовой модуляцией. Следует сразу оговориться, что QPSK и 4-QAM на самом деле один и тот же вид модуляции.

В 16-позиционной QAM (16-QAM) существует по четыре сигнальных значения для каждой из квадратурных компонент I и Q. Этим достигаются шестнадцать значений суммарного сигнала.

Зная, что , получаем, что в 16-QAM одним символом могут быть переданы четыре бита. Это означает, что символьная скорость в таком виде модуляции получается в четыре раза меньше битовой, т. е. равна 1/4 от битовой скорости. Таким образом, данный тип модуляции позволяет организовать спектрально более эффективную передачу данных. Векторная диаграмма сигнала 16-QAM приведена на рисунке 1.

Рисунок 1. Векторная диаграмма сигнала 16-QAM

Точно так же, как и в других системах модуляции в 16-QAM применяется кодирование Грея. Соответствие сигнальных созвездий, кода Грея и цифровых значений сигналов I и Q для 16-QAM, приведено на рисунке 2.

Рисунок 2. Соответствие сигнальных созвездий, кода Грея и цифровых значений сигналов I и Q для 16-QAM

Глазковая диаграмма сигналов I и Q для 16-позиционной квадратурной модуляции 16 QAM приведена на рисунке 3.

Рисунок 3. Глазковая диаграмма сигналов I и Q 16-позиционной квадратурной модуляции 16 QAM

В 16-ти позиционной QAM (16-QAM) существует по четыре сигнальных значения для каждой из квадратурных компонент I и Q. Этим достигаются 16 значений суммарного сигнала.

Для иллюстрации, на рисунке 4 приведена фотография экрана измерительного прибора — векторного анализатора. На этом рисунке видны векторная, глазковая диаграмма и основные характеристики сигнала 16-QAM на частоте 450 МГц.

Рисунок 4. Экран векторного анализатора, на котором видны векторная, глазковая диаграмма и основные характеристики сигнала 16-QAM на частоте 450 МГц

Еще одна разновидность QAM — это 32-QAM. Ее характеристики таковы: по шесть сигнальных значений для I и для Q, что в итоге дает точек созвездия для суммарного сигнала. Сигнальное созвездие сигнала 32-QAM приведено на рисунке 5.

Рисунок 5. Сигнальное созвездие сигнала 32-QAM

Этот тип модуляции наделен особенностью. В итоге, количество значений 36 не соответствует исходным данным, т.к. слишком велико, (). Поэтому, четыре «угловых» сигнальных значения, (на которые приходится большинство мощности передатчика), опущены. Этим уменьшается значение выходной мощности, которую должен генерировать передатчик. Исходя из того, что , получаем битовую скорость, равную 5 бит/с и символьную скорость, равную 1/5.

Особенность сигналов QAM — это возможность увеличивать количество сигнальных точек в обмен на помехоустойчивость. В результате в одной и той же полосе сигналов есть возможность увеличивать скорость передачи цифровой информации. Ограничение на увеличение пропускной способности канала накладывает только сложность реализации аппаратуры телекоммуникационных устройств

Дата последнего обновления файла 31.01.2020

Понравился материал? Поделись с друзьями!

Steve C. Cripps RF Power Amplifiers for Wireless Communications — ARTECH HOUSE, INC., 2006
Marian K. Kazimierczuk RF Power Amplifiers — John Wiley & Sons, Ltd 2008
Радиопередающие устройства: учебник для ВУЗов; под ред. В. В. Шахгильдяна. — 3-е изд., перераб. и доп. — М.: Радио и связь, 2003.

Вместе со статьей «Квадратурная модуляция (QAM)» читают:

MSK-модуляция частотная с минимальным сдвигом по частоте
https://digteh.ru/UGFSvSPS/modul/MSK/

Предыдущие версии сайта:
http://neic.nsk.su/

Об авторе:
к.т.н., доц., Александр Владимирович Микушин

Кандидат технических наук, доцент кафедры САПР СибГУТИ. Выпускник факультета радиосвязи и радиовещания (1982) Новосибирского электротехнического института связи (НЭИС).

А.В.Микушин длительное время проработал ведущим инженером в научно исследовательском секторе НЭИС, конструкторско технологическом центре «Сигнал», Научно производственной фирме «Булат». В процессе этой деятельности он внёс вклад в разработку систем радионавигации, радиосвязи и транкинговой связи.

Научные исследования внедрены в аппаратуре радинавигационной системы Loran-C, комплексов мобильной и транкинговой связи «Сигнал-201», авиационной системы передачи данных «Орлан-СТД», отечественном развитии системы SmarTrunkII и радиостанций специального назначения.

Источник

Квадратурная амплитудная модуляция. При квадратном созвездии модуляции N-QAM (см

При квадратном созвездии модуляции N—QAM (см. [29, 35]):

≡ P_кв(M ) = ,

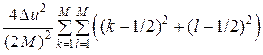
или P_кв(M ) = 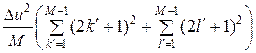= Δu 2 (2 M – 1) (2 M + 1)/6, (18.1)

где U₀ – диагональ квадрата созвездия N-QAM; Δu – расстояние между соседними позициями по горизонтали или по вертикали; .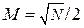

Но ; значит, P_кв(M ) = .

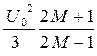
Например, при M = 1 (четырёхпозиционная фазовая манипуляция 4-PSK ) P_кв(M ) = P_кв(1) = 3U₀ 2 /3 = U₀ 2 , что очевидно.

При M → ∞: P_кв(M ) = P_кв(∞) = U₀ 2 /3, что соответствует дисперсии равномерного распределения случайной величины на квадрате с диагональю 2 U₀.

Таким образом, при модуляции N-QAM с квадратным созвездием отношение сигнал/помеха есть: Q = Δu 2 (2 M – 1) (2 M + 1)/(3 r 2 ). Величина пропускной способности C_ц соответствует величине Δu = 2 r ; отсюда получаем:

Результаты расчётов зависимостей C_ц(Q) = 2 F_Н log (1 + 3 Q/4) и N₀(Q) = = 1 + 3 Q/4 показаны на рис. 31 и 32 кривыми 2.

бит С_ц

знак

7

6

5 ШЦ2

4

1

3

Ш

2

1

0

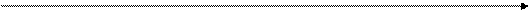
Q

Рис. 31. Сравнительная оценка пропускной способности

современных цифровых каналов радиосвязи

При гексагональном созвездии модуляции N-QAM величина N приобретает следующий ряд значений: N = 6, 18, 36, 60, 90, 128 и т. д. Поэтому при каждом из них, исходя из гексагональной конфигурации созвездия, можно получить соответствующий ряд значений 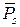: 4 r 2 ; 32 r 2 /3; 123 r 2 /6; 284 r 2 /10; и т. д.

Читайте также: Где находиться созвездие рака
Результаты расчётов зависимостей C(Q) и N₀(Q) для гексагонального созвездия N-QAM показаны на рис. 31 и 32 кривыми 3. Для сопоставления полученных оценок на рис. 31 приведена также зависимость – формула К. Шеннона (кривая Ш ) а также C_ц(Q) = 2 C(Q) – кривая ШК.

N₀

120

100

80

60 3

40 2

20 1

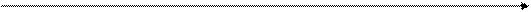
Q

Рис. 32. Сравнительная оценка оптимального количества сигнальных позиций

современных цифровых каналов радиосвязи

Таким образом, сравнительные оценки пропускной способности современных цифровых каналов радиосвязи, проведённые предложенным в разд. 12 упрощенным методом, позволяют сделать следующие выводы (см. рис. 31 и 32).

1. Современные цифровые каналы радиосвязи обладают значительно большей пропускной способностью, чем аналоговые, для которых формула Шеннона даёт верхнюю границу при больших значениях отношения сигнал/помеха Q. Например, при значениях Q > 10 модуляция N—PSK даёт относительно формулы Шеннона на 1,15 (бит/с) большее значение величины C(Q).

Более точные оценки (см. ниже) дают выигрыш около 0,8 (бит/с).

2. При значениях отношения сигнал/помеха Q, меньших 10, следует применять фазовую манипуляцию N-PSK: от двухпозиционной до восьмипозици-

онной. При величине Q ≥ 20 целесообразно перейти к 16-позиционной квадратурной амплитудной модуляции с квадратным созвездием. На гексагональное созвездие, которое довольно сложно в реализации, лучше всего переходить при Q ≥ 50. В последнем случае пропускная способность аналоговых каналов радиосвязи при Q = 100 ограничена величиной 3,3, а цифровых каналов – величиной 6,5 (бит/с).

3. Проведённые сравнительные характеристики пропускной способности C_ц(Q) и оптимального количества позиций N₀(Q) цифровых систем электросвязи требуют уточнения, поскольку для реальных линий электросвязи характерны помехи, распределение которых в первом приближении следует аппроксимировать гауссовским законом.

Дата добавления: 2015-05-16 ; просмотров: 633 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник