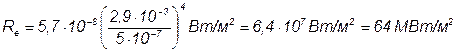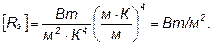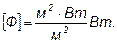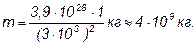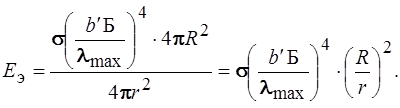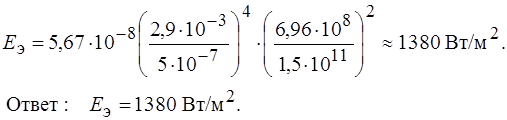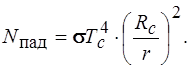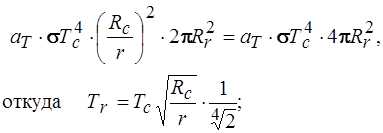Максимум спектральной плотности энергетической светимости солнца определить
Задача 539. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

Пример 2. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Мe Солнца; 2) поток энергии Фe, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.

Задачи для самостоятельного решения:
1. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость ослабла в 16 раз.
2. Температура внутренней поверхности муфельной печи при при открытом отверстии площадью равна Т. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая мощность составляет Р.
3. Определить, как и во сколько раз изменится излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с л1 до л2
4. Площадь, ограниченная графиком спектральной плотности энергетической светимости r(л,Т) черного тела, при переходе от термодинамической температуры Т1 к температуре Т2 увеличилась в 5 раз. Определить, как изменится при этом длина волны лmax, соответствующая максимуму спектральной плотности энергетической светимости черного тела.
5. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилось с л1, до л2. Определить, во сколько раз увеличилась: 1). энергетическая светимость тела; 2). максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает по закону (r(л,Т))max=СТ^5, где С извесная постоянная величина.
6. Определить, какая длина волны соответствует максимальной спектральной плотност энергетической светимости (r(л,Т))max (С – постояннай в законе, связывающем максимальную спектральную плостность энергетической чветимости черного тела с термодинамической температурой и равна 1,3*10^(-5) Вт(м^3*K^5). 7. Считая никель черным телом, определите мощность, необходимую для поддержания температуры расплавленного никеля t неизменной, если площадь его поверхности равна S. Потерями пренебречь
8. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответстует длина волны л, определить: 1). температуру поверхности Солнца; 2). энергию, излучаемую Солнцем в виде электромагнитных волн за время t; 3) массу, теряемую Солнцем за это время за счёт излучения.
9. Определить темепратуру тела, при которой оно при температуре окружающей среды t0 излучало энергии в n раз больше чем поглощало.
10. Считая, что тепловые потери обусловлены только излучением, опеределите, какую мощность необходимо подводить к медному шарику диаметром d, чтобы при температуре окружающей среды t0 поддерживать его температуру равной t. Примите поглощательную способность меди Аr.
11. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d, температура которой в вакууме поддердивается постоянной и равной t. Поверхность проволоки считать серой с поглощательной способностью Ar. Удельное сопротивление проволоки при данной температуре ро. Температура окружающей проволоку среды t0
12. Используя формулу Планка, определите спектральную плотность потока излучения еденицы поверхности черного тела, приходящегося на узкий интервал длин волн дл около максимума спектральной плотности энергетической светимости, если температура черного тела T.
13. Для вольфрамовой нити при температуре T поглощательная способность Ar. Определить радиационную температуру нити.
14. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0.
Источник
Пример 31



Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны l » 5000 ангстрем. Принимая Солнце за абсолютно черное тело, определить: 1) энергетическую светимость Солнца; 2) поток энергии, излучаемой Солнцем; 3) массу электромагнитных волн (всех длин), излучаемых Солнцем за одну секунду.


Ф,Rэ, m = ? тела выражается формулой Стефана-Больцмана:
где s — постоянная Стефана-Больцмана; Т – абсолютная температура излучающей поверхности.
Температура может быть определена из закона смещения Вина:
где l0 — длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела; b – постоянная Вина.
Выразив из закона смещения Вина температуру Т и подставив ее в формулу (1), получим:
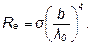
Подставив числовые значения в выражение (2) и произведя вычисления, получим:
2. Поток энергии Ф, излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности:
где r – радиус Солнца.
Подставив числовые значения в формулу (3), найдем:
Ф = 4 . 3,14 . (7 . 10 8 ) 2. ×6,4 . 10 7 Вт = 3,9×10 26 Вт.
3. Массу электромагнитных волн (всех длин), излучаемых Солнцем за 1 с определим, применив закон пропорциональности массы и энергии:
Энергия электромагнитных волн, излучаемых за время t, равна произведению потока энергии (мощности излучения) на время
Следовательно, Фt = mc 2 , откуда m = Фt/c 2 .
Сделав подстановку числовых значений величин, найдем:
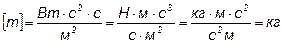
Источник
Примеры решения задач. Задача 15. Исследование спектра излучения Солнца показало, что максимум спектральной плотности энергетической светимости соответствует длине волны 0,5 мкм
Задача 15. Исследование спектра излучения Солнца показало, что максимум спектральной плотности энергетической светимости соответствует длине волны 0,5 мкм. Определить энергетическую освещенность поверхности Земли, принимая Солнце за абсолютно черное тело.
| Дано: lmax = 0,5 мкм = 5 × 10 –7 м rc = 6,96 × 10 8 м r = 1,5 × 10 11 м s = 5,67×10 –8 Вт/(м 2 ×К 4 ) | Решение Энергетическая освещенность поверхности Земли равна потоку солнечной энергии, падающей на единицу поверхности Земли. Будем считать Солнце сферой, площадь поверхности которой |
| Еэ – ? | S = 4 p rc 2 . |
Поток энергии, излучаемой Солнцем,
Фс = Rэ × 4 p R 2 ,
где Rэ = s . T 4 c, так как, по условию задачи, Солнце – абсолютно черное тело.
Фс = s . T 4 c × 4 p R 2 .
Температуру поверхности Солнца Тс определим из закона Вина
Тс = b΄/ lmax .
Поток солнечной энергии распространяется от Солнца по всем направлениям в пределах 4p радиан (в дальнейшем будем считать Солнце точечным источником). На единицу любой поверхности находящейся на расстоянии r от Солнца, приходится энергия, равная Фс / (4p . r 2 ) .
Задача 16. Внутри солнечной системы на том же расстоянии от Солнца, как и Земля, находится частица сферической формы. Полагая Солнце абсолютно черным телом с температурой Тс = 6000 К и что температура частицы во всех ее точках одинакова, определить ее температуру, считая частицу серым телом.
| Дано: r = 1,5 . 10 11 м Тс = 6000 К Rс = 6,96 . 10 8 м l= 500 нм | Решение Частица – серое тело, следовательно, ее поглощательная способность одинакова для всех длин волн и при данной температуре частиц аl,Т = аT . Так как температура частицы постоянна во всех ее точках, соблюдается условие равновесия: |
| Тr – ? | мощность излучения, поглощаемого частицей, равна |
мощности излучения, испускаемой ею
Определим Nпогл, исходя из объяснения решения предыдущей задачи. Мощность солнечного излучения, падающего на единицу поверхности частицы, равна
Если учесть, что к Солнцу обращена половина поверхности частицы, то на поверхность частицы падает мощность солнечного излучения, равная
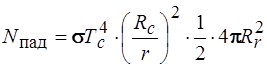
где Rc – радиус частицы.
Частица – это серое тело, поэтому она поглощает не всю энергию, а только часть ее.
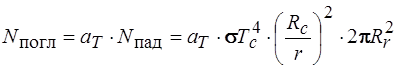
Определим энергию, излучаемую частицей
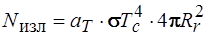
Приравнивая правые части последних соотношений, получим
Задача 17. Определить, за какое время зачерненный металлический шар диаметром D остынет с температуры T1 до температуры T2. Теплоемкость шара С. Остывание идет только за счет теплового излучения.
Теплоемкость твердого тела определяется формулой
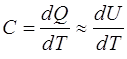
где dU – это изменение внутренней энергии, так как при нагревании происходит незначительное изменение объема тела.
Вследствие теплового излучения происходит убыль внутренней энергии шара, равная d U = – C d T .
С другой стороны, энергия, излучаемая нагретым шаром за время dt, равна dE = s T 4 × 4p R 2 ×d t .
Приравнивая правые части последних соотношений, получим
– C d T = s T 4 × 4p R 2 ×d t.
Проводим разделение переменных и решаем полученные интегралы
Источник
Электронная библиотека
Пример 1. Максимум спектральной плотности энергетической светимости Солнца приходится на длину волны l = 0,48 мкм. Считая, что Солнце излучает как черное тело, определить: 1) температуру его поверхности; 2) мощность, излучаемую его поверхностью.
Решение. Согласно закону смещения Вина, искомая температура поверхности Солнца , где b = 2,9 10 -3 м ×К – постоянная Вина.
Мощность, излучаемая поверхностью Солнца, равна:
где – энергетическая светимость черного тела (Солнца); – площадь поверхности Солнца. Согласно закону Стефана-Больцмана, , где = 5,67 10 -8 Вт/(м 2 К 4 ) – постоянная Стефана-Больцмана.
Подставив записанные выражения в формулу (1), найдем искомую мощность, излучаемую поверхностью Солнца:
Вычисляя, получим: 1) = 6040 К, 2) = 4,58 10 26 Вт.
Пример 2. Натрий освещается монохроматическим светом с длиной волны = 40 нм. Определить наименьшее задерживающее напряжение ( ), при котором фототок прекратится.
«Красная граница» фотоэффекта для натрия = 584 нм.
Решение. Задерживающее напряжение можно определить из выражения:
где е = 1,6×10 -16 Кл – заряд электрона. Кинетическую энергию электрона определим из уравнения Эйнштейна:
где А – работа выхода;
Подставив формулу (3) в (2), получим:
Подставив формулу (4) в (1), найдем искомое задерживающее напряжение:
Вычисляя, получим: = 28,9 В.
Пример 3. Определить максимальное изменение длины волны при комптоновском рассеянии света на свободных электронах.
Решение. Для определения максимального изменения длины волны воспользуемся формулой Комптона:
где — изменение длины волны фотона в результате рассеяния на свободном электроне; h – постоянная Планка, m0 – масса покоя электрона; с— скорость света в вакууме; θ – угол рассеяния фотона, для определения максимальной длины волны угол рассеяния равен 180 градусов, тогда получим:
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Источник