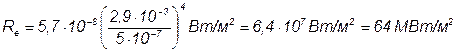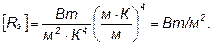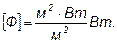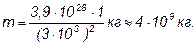Масса электромагнитных волн излучаемых солнцем

Задача 539. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

Пример 2. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Мe Солнца; 2) поток энергии Фe, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.

Задачи для самостоятельного решения:

1. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость ослабла в 16 раз.

2. Температура внутренней поверхности муфельной печи при при открытом отверстии площадью равна Т. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая мощность составляет Р.

3. Определить, как и во сколько раз изменится излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с л1 до л2

4. Площадь, ограниченная графиком спектральной плотности энергетической светимости r(л,Т) черного тела, при переходе от термодинамической температуры Т1 к температуре Т2 увеличилась в 5 раз. Определить, как изменится при этом длина волны лmax, соответствующая максимуму спектральной плотности энергетической светимости черного тела.

5. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилось с л1, до л2. Определить, во сколько раз увеличилась: 1). энергетическая светимость тела; 2). максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает по закону (r(л,Т))max=СТ^5, где С извесная постоянная величина.

6. Определить, какая длина волны соответствует максимальной спектральной плотност энергетической светимости (r(л,Т))max (С – постояннай в законе, связывающем максимальную спектральную плостность энергетической чветимости черного тела с термодинамической температурой и равна 1,3*10^(-5) Вт(м^3*K^5). 7. Считая никель черным телом, определите мощность, необходимую для поддержания температуры расплавленного никеля t неизменной, если площадь его поверхности равна S. Потерями пренебречь

8. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответстует длина волны л, определить: 1). температуру поверхности Солнца; 2). энергию, излучаемую Солнцем в виде электромагнитных волн за время t; 3) массу, теряемую Солнцем за это время за счёт излучения.

Читайте также: Лицо загорает без солнца

9. Определить темепратуру тела, при которой оно при температуре окружающей среды t0 излучало энергии в n раз больше чем поглощало.

10. Считая, что тепловые потери обусловлены только излучением, опеределите, какую мощность необходимо подводить к медному шарику диаметром d, чтобы при температуре окружающей среды t0 поддерживать его температуру равной t. Примите поглощательную способность меди Аr.

11. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d, температура которой в вакууме поддердивается постоянной и равной t. Поверхность проволоки считать серой с поглощательной способностью Ar. Удельное сопротивление проволоки при данной температуре ро. Температура окружающей проволоку среды t0

12. Используя формулу Планка, определите спектральную плотность потока излучения еденицы поверхности черного тела, приходящегося на узкий интервал длин волн дл около максимума спектральной плотности энергетической светимости, если температура черного тела T.

13. Для вольфрамовой нити при температуре T поглощательная способность Ar. Определить радиационную температуру нити.

14. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0.

Источник

Задача №1. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны l = 500 нм

Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны l = 500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Солнца; 2) поток энергии Ф_е, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.

Энергетическая светимость R черного тела выражается формулой Стефана – Больцмана

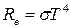
Температура излучающей поверхности может быть определена из закона смещения Вина

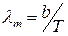
Выразив отсюда температуру Т и подставив ее в закон Стефана – Больцмана, получим

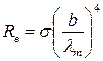
Произведя вычисления по этой формуле, получим R_e = 64 МВт/м 2 .

Поток энергии Ф_е, излучаемый Солнцем, равен произведению энергетической светимости R на площадь поверхности солнца S

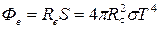
где R_C = радиус Солнца. Подставляя в последнюю формулу численные значения, получим Ф_е = 3,9×10 26 Вт.

Массу электромагнитных волн (всех длин), излучаемых Солнцем за время Dt, определим, применив закон пропорциональности массы и энергии

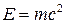
С другой стороны, энергия электромагнитных волн, излучаемых за время Dt, равна произведению потока энергии Ф_е (мощности излучения) на время

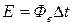
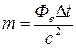
Произведя вычисления, получим m = 4,3×10 9 кг.

Источник

Пример 31

Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны l » 5000 ангстрем. Принимая Солнце за абсолютно черное тело, определить: 1) энергетическую светимость Солнца; 2) поток энергии, излучаемой Солнцем; 3) массу электромагнитных волн (всех длин), излучаемых Солнцем за одну секунду.

Дано: Решение

l » 5 . 10 -7 м 1. Энергетическая светимость R_э абсолютно черного

Ф,R_э, m = ? тела выражается формулой Стефана-Больцмана:

где s — постоянная Стефана-Больцмана; Т – абсолютная температура излучающей поверхности.

Температура может быть определена из закона смещения Вина:

где l₀ — длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела; b – постоянная Вина.

Выразив из закона смещения Вина температуру Т и подставив ее в формулу (1), получим:

(2)

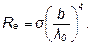
Подставив числовые значения в выражение (2) и произведя вычисления, получим:

2. Поток энергии Ф, излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности:

где r – радиус Солнца.

Подставив числовые значения в формулу (3), найдем:

Ф = 4 . 3,14 . (7 . 10 8 ) 2. ×6,4 . 10 7 Вт = 3,9×10 26 Вт.

3. Массу электромагнитных волн (всех длин), излучаемых Солнцем за 1 с определим, применив закон пропорциональности массы и энергии:

Энергия электромагнитных волн, излучаемых за время t, равна произведению потока энергии (мощности излучения) на время

Следовательно, Фt = mc 2 , откуда m = Фt/c 2 .

Сделав подстановку числовых значений величин, найдем:

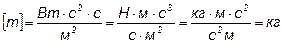
Источник

Масса электромагнитных волн излучаемых солнцем

Название: квантовая оптика (Э. Б. Селиванова, В. Я. Чечуев)

15.3. примеры решения задач

Задача 15.3.1. Определите длину волны, соответствующую максимуму энергии излучения лампы накаливания. Нить накала имеет длину = 15 см и диаметр d = 0,03 мм. Мощность, потребляемая лампой,

Р = 10 Вт. Нить лампы излучает как серое тело с коэффициентом поглощения aс = 0,3; 20\% потребляемой энергии передается другим телам вследствие теплопроводности и конвекции.

Из правила смещения Вина следует

lmax = , (4)

Температуру нити найдем, используя закон Стефана-Больцмана. Применительно к данному случаю он запишется в виде

0,8Р = aсsТ4p×d×. (5)

Выразив Т из соотношения (5) и, подставив в (4), получим

lmax =С¢ .

Задача 15.3.2. Определите мощность излучения раскаленной вольфрамовой нити с температурой Т = 2000 К в интервале длин волн, отличающихся от длины волны, соответствующей максимуму излучения на 1\%. Площадь поверхности нити S = 1,5×10-5м2, коэффициент серости вольфрама aс = 0,26.

В рассмотренном случае мощность излучения в интервале длин волн Dl, очевидно, равна

РDl = aс×, (6)

где , (7)

, (8)

. (9)

Подставляя (7), (8), и (9) в (6), будем иметь

Задача 15.3.3. Максимум излучения абсолютно черного тела при нагревании переместился с l1 = 0,8 мм на l2 = 0,6 мм. Определите во сколько раз изменилась спектральная плотность энергетической светимости.

Согласно закону Вина

. (10)

Для определения температуры воспользуемся правилом смещения Вина

Т = . (11)

Подставив (11) в (10) и взяв отношение двух значений спектральной плотности энергетической светимости, получим

Задача 15.3.4. Исследование спектра излучения Солнца показали, что максимум спектральной плотности энергетической светимости соответствует длине волны 5000 Ао. Принимая Солнце за абсолютно черное тело, определите:

1) энергетическую светимость Солнца Rэ;

2) поток энергии, излучаемой Солнцем;

3) массу электромагнитных волн всех длин, излучаемых Солнцем за 1 с.

1. Энергетическая светимость абсолютно черного тела определяется законом Стефана-Больцмана

Неизвестную в (12) температуру найдем из правила смещения Вина

. (13)

Подставляя (13) в (12), получим

Rэ= s.

2) Поток энергии, излучаемой Солнцем, равен произведению энергетической светимости на площадь поверхности Солнца (rсолнца = 7×108 м)

Ф = Rэ×S = Rэ×4p×= 6,4 ×107×4×3,14(7×108)2=3,9×1026 Вт.

3) Массу электромагнитных волн всех длин, излучаемых Солнцем за 1с, найдем из соотношения Эйнштейна между энергией и массой

где Е – энергия, излучаемая Солнцем за 1с;

Из (14) и (15) следует

m =

Задача 15.3.5. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела lmax = 5,8×10-7м. Определите:

1) энергетическую светимость поверхности тела;

2) спектральную плотность энергетической светимости , рассчитанную вблизи lmax на интервал длин волн Dl = 1 нм.

1. Энергетическую светимость определим по закону Стефана-Больцмана с учетом правила смещения Вина

Rэ = sT 4, lmax = .

Тогда Rэ = s.

2. Спектральную плотность энергетической светимости вблизи максимума найдем по соотношению

= С²T 5, (16)

где С²= 1,3×10-14 Вт/м2×нм×К5 (17)

Подставляя (17) в (16) и заменяя Т по правилу смещения, получим

= С²×.

Содержание

Читать: Аннотация
Читать: Тема 15. тепловое излучение
Читать: 15.1. основные понятия и соотношения
Читать: 15.2. контрольные вопросы
Читать: 15.3. примеры решения задач
Читать: Тема 16. фотоэффект. давление света.эффект комптона
Читать: 16.1.основные понятия и соотношения
Читать: 16.2. примеры решения задач

Источник