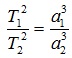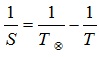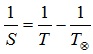Масса Луны
Из всех параметров небесных тел масса – самый сложный для вычислений. Поэтому, в отличие от диаметра, масса Луны была рассчитана относительно недавно.
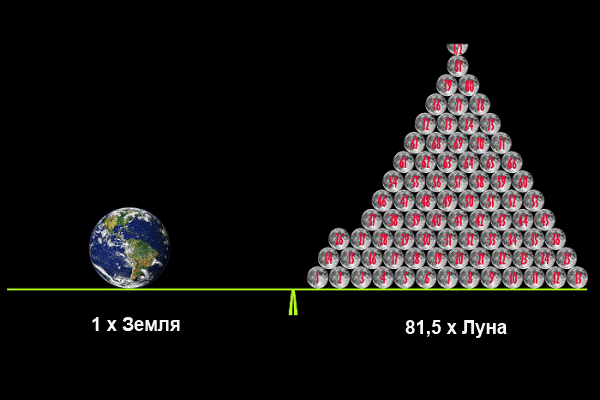
Среди спутников Солнечной системы Луна стоит на шестом месте по массе. Её масса составляет 7,34х1022 кг, что в 80 раз меньше земной. Можно рассчитать среднюю плотность Луны — 3,35 г/см3,что в 3-4 раза больше, чем у других спутников (кроме Ио – спутника Юпитера), а также ускорение свободного падения – 1,62 м/с2, и силу тяжести, которая равна 1/6 земной, то есть предмет, перемещённый с Земли на её спутник, стал бы весить в шесть раз меньше. Из-за слабого притяжения у Луны нет атмосферы.
Гравитационное влияние
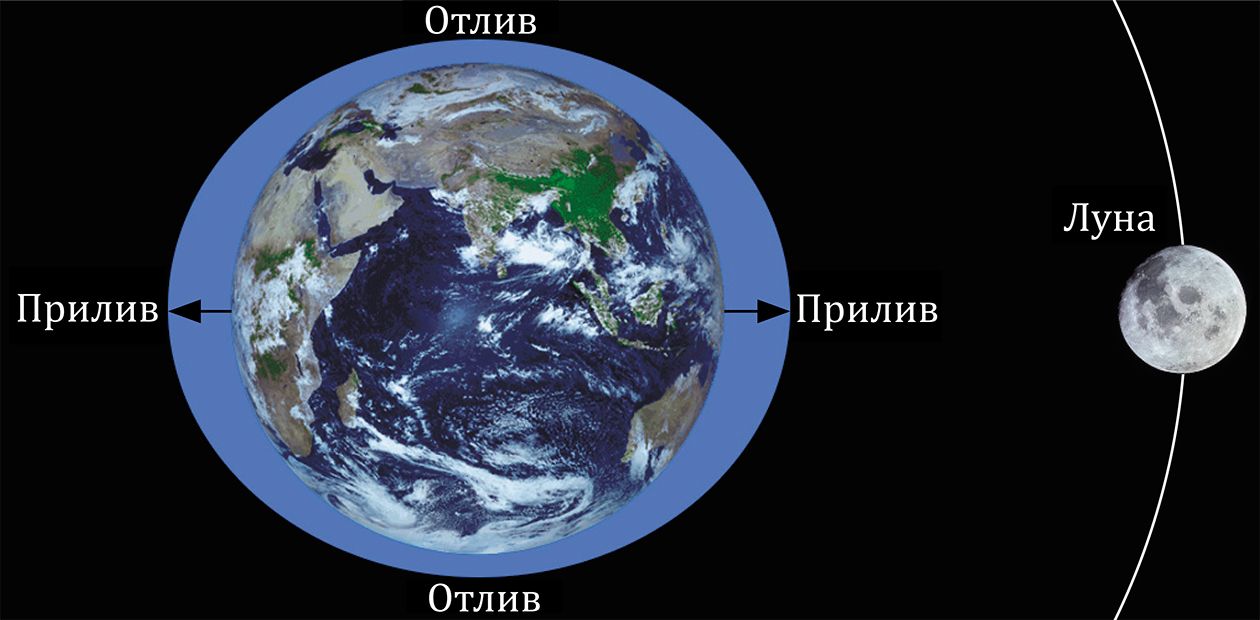
Приливы и отливы
Луна – аномально крупный и массивный спутник, поэтому она оказывает ощутимое гравитационное воздействие на планету. Основным проявлением такого воздействия являются приливы и отливы.
Вдоль оси Луна – Земля возникают «приливные» силы. Чем участок Земли ближе к Луне, тем сильнее он к ней притягивается. Разная степень притяжения в разных точках вызывает деформацию земного шара, в результате возникают морские приливы и отливы.
Как результат, гравитация Луны влияет на земную кору, атмосферу и гидросферу Земли и даже на её геомагнитное поле.
Земля с Луной образуют единую систему масс, центр которой расположен на расстоянии 4750 км от центра Земли.
Как измерили
Масса Луны в сравнении с Землей
Первым попытался рассчитать массу Луны Ньютон, используя измерения, проведённые во время морских приливов, но получил результат, превышающий истинное значение в два раза. Правильно вычислить массу спутника смогли после того, как Кавендиш экспериментально определил точное значение гравитационной постоянной.
‘ alt=»yH5BAEAAAAALAAAAAABAAEAAAIBRAA7 — Масса Луны» title=»Масса Луны»>
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Источник
§ 30. Примеры решения задач по теме «Закон всемирного тяготения
При решении задач надо помнить, что сила тяготения действует между любыми телами, имеющими массу, но формула 
справедлива только для тел, которые можно считать материальными точками, а также для однородных тел шаровой формы. При этом расстояние r — это расстояние между центрами шаров.
Задача 1. При опытной проверке закона всемирного тяготения сила взаимодействия между двумя свинцовыми шарами массами m1 = 5 кг и m2 = 500 г, расстояние между центрами которых r = 7 см, оказалась равной F = 34 нН. Вычислите по этим данным гравитационную постоянную.
Р е ш е н и е. Согласно закону всемирного тяготения 
Из этого выражения следует, что 
Подставим в эту формулу результаты опыта, при этом все данные переведём в СИ: m2 = 500 г = 5 • 10 -1 кг, r = 7 см = 7 • 10 -2 м, F = 34 нН = 3,4 • 10 -8 Н.
Получим 
Уточнённое значение гравитационной постоянной, которое входит в таблицы: 
Задача 2. Определите равнодействующую силу, действующую на Луну, считая, что силы притяжения к Земле и Солнцу взаимно перпендикулярны. Массы Луны, Земли и Солнца соответственно равны mЛ = 7,36 • 10 22 кг; m3 = 5,98 • 10 24 кг; mC = 1,99 • 10 30 кг; расстояния от Луны до Земли и от Луны до Солнца соответственно равны rЛЗ = 3,85 • 10 8 м, rЛС = 1,5 • 10 11 м.
Р е ш е н и е. По условию задачи силы гравитационного притяжения Луны к Земле и Солнцу взаимно перпендикулярны (рис. 3.6). Рассчитаем силу гравитационного притяжения Луны к Земле.
Сила притяжения Луны к Солнцу равна
По теореме Пифагора найдём равнодействующую силу, действующую на Луну,
Задача 3. На поверхности Земли находятся два свинцовых шара радиусом R = 10 см каждый. В одном из них вырезана сферическая полость, как показано на рисунке 3.7. Радиус полости r = 5 см, центр полости находится на расстоянии l = 5 см от центра шара. Определите силу гравитационного притяжения шаров. Центры шаров находятся на расстоянии L = 40 см.
Р е ш е н и е. Если бы у правого шара не было вырезанной полости, то сила гравитационного притяжения шаров была бы равна 
при этом 
Вырезав полость, мы уменьшаем эту силу притяжения на силу F2, равную силе притяжения левого шара к вырезанной части:
Заметим, что L = 4R = 8r; R = 2r, соответственно m = 8 m1.
Подставив эти выражения в формулу (1), получим
Учтя, что 
получаем 
Задачи для самостоятельного решения
1. Радиус R1 Луны примерно в 3,7 раза меньше, чем радиус R Земли, а масса m Луны в 81 раз меньше массы М Земли. Определите ускорение свободного падения тел на поверхности Луны.
2. Предположим, что масса Земли стала в 2 раза, а радиус — в 1,2 раза больше. Определите, во сколько раз изменилась сила тяжести, действующая на тело, находящееся на полюсе.
Образцы заданий ЕГЭ
С1. Какое ускорение сообщает Солнце Земле своим притяжением? Расстояние до Солнца примерно в 24 000 раз больше, чем радиус Земли, а масса Солнца превышает массу Земли в 333 000 раз. (g3 = 10 м/с 2 .)
С2.Вычислите ускорение Луны, движущейся вокруг Земли по окружности. Расстояние между центрами Земли и Луны примите равным 400 000 км. Радиус Земли 6400 км. (g3 = 10 м/с 2 .)
Источник
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Есть только два способа прожить жизнь. Первый — будто чудес не существует. Второй — будто кругом одни чудеса.
А.Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля
Список лекций по физике за 1,2 семестр
Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
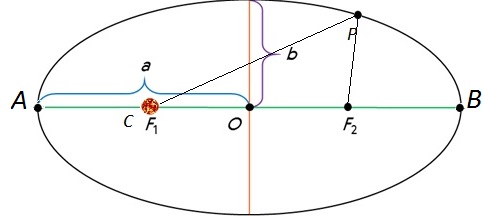
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
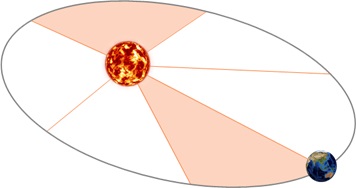
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
,
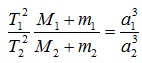
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
,
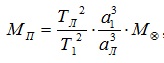
где Тл и α л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Источник
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Вопросы к экзамену
Для всех групп технического профиля
Список лекций по физике за 1,2 семестр
Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
,
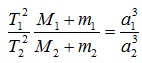
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
,
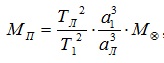
где Тл и α л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Источник