Во сколько раз Солнце превосходит Землю по массе, площади, радиусу и объему?
Солнце является самым массивным объектом в Солнечной системе, и оно значительно больше Земли. Но во сколько раз оно превосходит нашу планету по размерам?
Если говорить о радиусах Земли и Солнца, то у нашей звезды он равен 695 тыс. км, в то время как земной радиус оценивается всего лишь в 6371 км. Таким образом, радиус Солнце превосходит земной аж в 109 раз.
Ситуация изменится, если мы сравним площади поверхностей звезды и планеты. Так как площадь сферы пропорциональна квадрату ее радиуса, то и площадь Земли теоретически должна оказаться в 1092 = 11881 раз меньше площади солнечной поверхности. Однако в реальности ни Земля, ни Солнца не являются абсолютно идеальными сферами, поэтому на самом деле звезда превосходит нашу планету по площади в 11 918 раз.
Сравнение по объему окажется ещё более невыгодным для Земли. Объем Солнца превосходит земной аж в 1 301 019 раз! Это связано с тем, что объем сферы пропорционален уже кубу ее радиуса.
Наконец, можно оценить и массы двух небесных тел. С одной стороны, масса пропорциональна объему. С другой стороны, она также определяется плотностью вещества. Земля состоит из твердых пород, а вот в химическом составе Солнца доминируют самые легкие элементы – водород и гелий. В результате средняя плотность звезды оказывается почти в 4 раза ниже плотности нашей планеты. В итоге же масса Земли меньше солнечной массы в 332 940 раз.
Как же ученые смогли определить массы и размеры Солнца, Земли и других планет? Ещё Эратосфен, живший в Древней Греции, смог достаточно точно оценить радиус Земли, измеряя угол наклона теней в полдень в разных городах. В XVII в. Ньютон сформулировал закон всемирного тяготения, из которого следовало, что все тела падают на Землю с одинаковым ускорением, причем зависит это ускорение от массы и радиуса Земли. Экспериментально определив ускорение свободного падения и зная (из расчетов Эратосфена) земной радиус, ученые смогли с помощью ньютоновской формулы оценить и массу Земли.
Наконец, с помощью того же закона тяготения можно оценить и массу Солнца, если известен радиус земной орбиты. Впервые он достаточно точно оценен в 1672 г. Джованни Кассино. Диаметр же Солнца можно определить, зная всё то же расстояние между Солнцем и Землей и измерив угловой размер звезды на небе.
Список использованных источников
Источник
Сравнение размеров Солнца и Земли
Для некоторых астрономических расчетов нужно знать, во сколько раз Солнце больше Земли. И на самом ли деле светило больше нашей планеты? Ведь мы видим его на небе в виде небольшого шарика.
Размер Земли и Солнца
Вес самой большой звезды в Солнечной системе составляет 2 октлн т (октиллион — число с 27 нулями по «короткой» шкале степеней тысячи, принятой в большинстве стран мира), и это составляет примерно 99,87% общей массы последней.
Земля весит намного меньше — 6 скстлн т (секстиллионов, это 10 в 21 степени по той же шкале). Простой расчет показывает: Солнце тяжелее нашей планеты в 333 тыс. раз.
Для измерения веса крупных космических объектов используются не тонны, а соответствующий параметр нашего светила — солнечная масса. Например, массивные звезды могут весить 5-10 солнечных масс, а супермассивные черные дыры — до сотни миллионов этих единиц.
Масса Солнца постепенно уменьшается из-за 2 специфических процессов, происходящих внутри него:
- в ядре непрерывно проходят реакции по преобразованию атомов водорода в гелий — это и есть ощущаемое нами тепло, и выделение энергии сопровождается потерей веса светила;
- солнечный ветер систематически выдувает из звезды во внешний космос электроны и протоны.
Второй процесс хорошо знаком ученым — было даже снято видео, как это происходит.
Диаметры объектов
Земля, имеющая средний радиус 6371 км, меньше даже одного солнечного ядра. Если сравнивать диаметры этих 2 объектов, по экваториальной оси Солнца можно расположить 109 наших планет.
Эти размеры центрального объекта Солнечной системы составляют:
- диаметр — около 1,391 млн км;
- радиус — около 695,5 тыс км.
При этом в сравнении с другими звездными телами наш желтый карлик считается относительно небольшим. Например, он меньше Альфа Ориона, красного супергиганта Бетельгейзе, в 1000 раз, а одной из звезд созвездия Большого Пса, красного гипергиганта VY, — в 2000 раз.
По аналогии с солнечной массой существует солнечный радиус — соотношение габаритов крупных астрономических объектов и нашего светила.
Сравнение гравитации
Солнце имеет наибольшую в своей системе гравитацию из-за своей массы — это значение в 28 раз выше земного.
Предмет массой 100 кг на солнечной поверхности весил бы 2,8 т. Для живых существ это явилось бы смертельным — их бы раздавило притяжением.
При этом сама звезда не сжимается — этому противостоят:
- «кипящая температура»;
- высокое давление;
- проходящий внутри светила ядерный синтез.
Солнечная гравитация настолько сильна, что удерживает на своей орбите даже находящийся на расстоянии около 6 млрд км от звезды Плутон.
И если бы не Облако Оорта, которое обволакивает нашу систему со всех сторон, Солнце могло бы притягивать объекты, расположенные даже на расстоянии до 2 световых лет от него.
Объем светила и планеты
Чтобы заполнить объем Солнца (1,4 нониллиона куб. км, число с 30 нулями) объектами, равными по размеру нашей планете, потребуется примерно 1,3 млн таких тел.
Объем нашего желтого карлика — величина постоянная. Но только до того момента, пока светило не выработает все водородное топливо в своем ядре.
Затем звезда начнет расширяться, превращаясь в красного гиганта. Она увеличится настолько, что поглотит орбиту Меркурия, а затем Венеры, впоследствии максимально приблизившись к Земле, возможно, поглотив и ее. Такое положение дел будет сохраняться несколько миллионов лет, в течение которых Солнце будет больше своего теперешнего размера в 200 раз.
Затем звезда сожмется и сравнительно быстро превратится в белого карлика. Сейчас ученые спорят о том, какой небесный объект тогда станет больше — Солнце или Земля.
Источник
Как измерить массу Земли и массу Солнца?
Простая и надежная методика измерения массы космических тел — как узнать сколько весит Солнце, зная лишь силу притяжения между космическими телами
Как можно измерить вес (точнее, массу) Солнца, если даже реальный размер нашей “домашней звезды” настолько велик, что просто не укладывается в голове? Наверняка тут должен быть какой-то секрет… И подумав так, вы будете правы и не правы одновременно.
На первый взгляд, идея измерить массу Солнца, кажется фантастикой. На самом деле для этого не понадобится ничего, кроме простейших вычислений
С одной стороны, никакого секрета в деле измерения массы любого небесного тела сколько угодно большого размера, конечно же нет. С другой стороны, без определенных хитростей тут, конечно, не обойтись.
Давайте сразу условимся – говоря, что “нам нужно определить массу Солнца”, мы имеем ввиду “определить количество вещества входящего в состав Солнца”.
Для начала измерим массу Земли
Переформулировав задачу таким образом, мы сразу же получим зацепки ведущие к решению. Первым делом нам нужно определить величину силы притяжения возникающей между любыми двумя массами.
Принцип этого определения следующий:
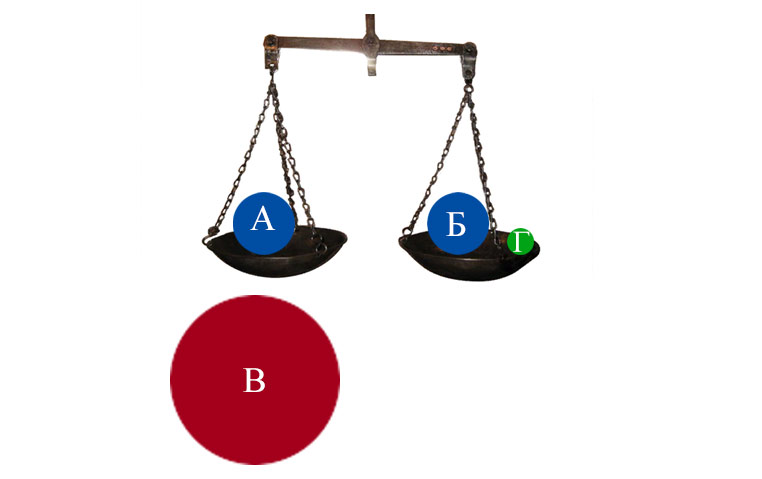
Представьте себе очень при очень чувствительные равноплечие весы с двумя чашками. В каждой чашке (А и Б) пускай лежит некий груз имеющий совершенно одинаковую массу. Весы в таком случае, будут прибывать в полном равновесии.
Теперь мы берем третье тело (В) масса которого нам также известна, и помещаем его под тело А. Взаимное притяжение между А и В, ожидаемо заставляет чашку весов А опуститься вниз. Для сохранения равновесия нам срочно необходимо добавить к массе Б очень небольшую, но опять же вполне измеримую массу Г.
Как вычислить массу планеты Земля, не выходя из дома?
Вас может заинтересовать
А вот теперь самое интересное: поскольку сила, с которой вся Земля притягивает тело Г, равна взаимному притяжению между А и В, можно без труда определить массу Земли, которая оказывается равной 6,59 х 10 21 тонн.
А теперь измерим массу Солнца!
Земля по своей орбите движется примерно так, как если бы невидимая нить соединяла ее с Солнцем. Действительно, гравитационное притяжение подобно натяжению нити, так что Земля все время движется к Солнцу, вместо того чтобы «улететь» по прямой линии, что будет, если эта “нить” вдруг оборвется. Можно сказать, что, двигаясь вокруг Солнца, Земля все время «падает» на него.
Этому “падению” соответствует отклонение ее орбиты от прямой линии, составляющее около 3 мм в секунду. Еще со времен Галилея известно, что на поверхности Земли в первую секунду своего падения всякое тело проходит 4,9 м. Расстояния 3 мм и 4,9 м прямо пропорциональны соответствующим гравитационным ускорениям, т. е. силам, действующим на единичную
массу со стороны Солнца на расстоянии Земли и Земли на ее поверхности.
Отсюда, зная, что гравитационное ускорение прямо пропорционально массе и обратно пропорционально квадрату расстояния от центра тела, можно легко вычислить, что масса Солнца в 329 390 раз больше массы Земли.
Воспользовавшись значением массы Земли, полученным выше, находим, что масса Солнца составляет 2.24 х 10 27 тонн. Полностью это немыслимое число можно записать, как 2 240 000 000 000 000 000 000 000 000 тонн.
Влияние силы тяготения на движение Земли. Путь А-С представляет собой путь пройденный Землей по орбите за 1 секунду (30 км), при этом отклонение от прямой линии B-C составит всего 3 миллиметра
Теперь уже можно вычислить и среднюю плотность Солнца, т. е. его массу, поделенную на массу воды, занимающей тот же объем.
Поскольку один кубический сантиметр воды весит один грамм, мы просто должны разделить массу Солнца (в граммах) на его объем (в кубических сантиметрах). Получим в результате число 1,42.
Иными словами, в среднем некоторый объем солнечного вещества должен весить приблизительно столько же, сколько ком битумного угля, занимающего такой же объем.
Естественно, “среднее значение” на то и среднее, чтоб представлять некую золотую середину между солнечным ядром (где плотность вещества в 10 раз превышает плотность стали) и веществом солнечной короны (где плотность падает почти до величины космического вакуума). Тем не менее, в общем и целом данная методика расчетов абсолютно верна и может с успехом применяться при расчете массы любого небесного тела – хоть астероида, хоть звезды.
Источник
Масса Земли в цифрах
Масса Земли достигает отметки в 5.9736 х 10 24 кг. Это крупное число, но, чтобы наш мозг попал в шоковое состояние, то в полном виде – 5 973 600 000 000 000 000 000 000 000 кг. Вау!
Как узнать массу Земли?
Но ведь интереснее узнать, как вообще смогли понять, какая масса Земли? Все дело в гравитации, которую наша планета оказывает на ближайшие объекты.
Физика говорит нам, что любые тела с массой притягиваются. Если вы положите рядом два бильярдных шарика, то они будут стремиться к соседнему. Эта сила не заметна нам, но приборы улавливают благодаря своей чувствительности. Это вычисление поможет вывести массу обоих.
Ньютон предположил, что масса сферических объектов сосредоточена в их центрах. Тогда можно воспользоваться уравнением:
- F – сила тяжести между ними.
- G – постоянная = 6.67259 × 10 -11 м 3 /кг с 2 .
- -M1 и M2 – притягивающиеся массы.
- R – дистанция между ними.
Допустим, что одна из масс представлена Землей, а второй будет килограммовая сфера. Сила между ними – 9.8 кг * м/с 2 . Земной радиус – 6 400 000 м. Если добавите эти значения в формулу, то получите 6 x 10 24 кг.
Важно отметить, что в вопросе правильно использовать слово «масса», а не «вес», потому что последнее понятие выступает силой, которая нужна для вычисления гравитационного поля. Можно взять мяч и взвесить его на Земле и Луне, и отметка будет меняться. Но масса – стабильное число и земная – постоянна.
Кажется, что это много, но не будем забывать, что в нашей системе есть объекты и крупнее. Например, наша звезда превосходит земную массу в 330000 раз, а Юпитер в 318 раз. Есть, конечно, и крошки. Так марсианская масса занимает лишь 11% земной.
Нам повезло из-за наивысшего показателя планетарной плотности в системе – 5.52 г/см 3 . Это значение досталось от металлического ядра, вокруг которого сосредоточен слой скалистой мантии. Менее плотные планеты, вроде гигантского Юпитера, представлены водородом и прочими газами. Теперь вы знаете чему равна масса Земли.
Источник
Планетная масса — Planetary mass
Планетарный масса является мерой массы в виде планеты объекта -подобного. В Солнечной системе , планеты, как правило , измеряется в астрономической системе единиц , где единица массы является масса Солнца ( M ☉ ), масса Солнца . При изучении экзопланет , единица измерения , как правило , масса Юпитера ( М J ) при больших газовых гигантских планет, и масса Земли ( M ⊕ ) для небольших каменистых планет земной .
Масса планеты в Солнечной системе — это настраиваемый параметр при подготовке эфемерид . Есть три варианта вычисления планетарной массы:
- Если у планеты есть естественные спутники , ее массу можно рассчитать с помощью закона всемирного тяготения Ньютона, чтобы получить обобщение третьего закона Кеплера, который включает массу планеты и ее луны. Это позволило на раннем этапе измерить массу Юпитера в единицах массы Солнца .
- О массе планеты можно судить по ее влиянию на орбиты других планет. В 1931-1948 годах ошибочные применения этого метода привели к неверным расчетам массы Плутона .
- Могут быть использованы данные о влиянии, собранные с орбит космических зондов . Примеры включают зондыVoyager к внешним планетам и космический корабль MESSENGER к Меркурию .
- Кроме того, множество других методов могут дать разумные приближения. Например, Варуна , потенциальная карликовая планета , очень быстро вращается вокруг своей оси, как и карликовая планета Хаумеа . Хаумеа должен иметь очень высокую плотность, чтобы его не раздирали центробежные силы . Посредством некоторых расчетов можно установить ограничение на плотность объекта. Таким образом, если размер объекта известен, можно определить предел массы. См. Ссылки в вышеупомянутых статьях для получения дополнительной информации об этом.
Содержание
Выбор единиц
Выбор солнечной массы , M ☉ , так как основная единица для планетарной массы поступает непосредственно из расчетов , используемых для определения планетарной массы. В наиболее точном случае, масса самой Земли , масса известна в единицах массы Солнца до двенадцати значащих цифр : одна и та же масса в килограммах или других единицах измерения на Земле известна только пяти значащим цифрам, которые меньше одной миллионной точности.
Разница заключается в том, как рассчитываются массы планет. Невозможно «взвесить» планету, а тем более Солнце, по эталонам массы, используемым в лаборатории. С другой стороны, орбиты планет дают большой диапазон наблюдательных данных относительно относительного положения каждого тела, и эти положения можно сравнить с их относительными массами, используя закон всемирного тяготения Ньютона (с небольшими поправками для общей теории относительности, где необходимо). Для того, чтобы преобразовать эти относительные массы в единицах наземного базирования , таких как килограмм, необходимо знать значение ньютоновской гравитационной постоянной , G . Эту константу чрезвычайно трудно измерить на практике, и ее значение известно только с точностью до одной десятитысячной.
Масса Солнца — довольно большая единица в масштабах Солнечной системы: 1,9884 (2) × 10 30 кг. Самая большая планета, Юпитер , составляет 0,09% массы Солнца, а Земля составляет около трех миллионных (0,0003%) массы Солнца. В литературе используются различные условные обозначения, чтобы решить эту проблему: например, инвертирование отношения, чтобы указать массу планеты в «количестве планет», которое потребуется для образования одного Солнца. Здесь мы решили перечислить все планетные массы в «микроСолнце» — то есть масса Земли составляет чуть больше трех «микроСолнц», или трех миллионных масс Солнца — если они специально не указаны в килограммах.
При сравнении планет между собой, часто бывает удобно использовать массу Земли ( М Е или М ⊕ ) в качестве стандарта, в частности , для земных планет . Для массы газовых гигантов , а также для большинства внесолнечных планет и коричневых карликов масса Юпитера ( M Дж ) является удобным сравнением.
| Планета | Меркурий | Венера | земной шар | Марс | Юпитер | Сатурн | Уран | Нептун |
|---|---|---|---|---|---|---|---|---|
| Масса Земли M ⊕ | 0,0553 | 0,815 | 1 | 0,1075 | 317,8 | 95,2 | 14,6 | 17,2 |
| Масса Юпитера М Дж | 0,000 17 | 0,002 56 | 0,003 15 | 0,000 34 | 1 | 0,299 | 0,046 | 0,054 |
Планетная масса и формирование планет
Масса планеты имеет последствия для ее структуры, поскольку имеет большую массу, особенно когда она находится в процессе формирования . Тело, которое составляет более одной десятитысячной массы Земли, может преодолеть свою прочность на сжатие и достичь гидростатического равновесия : оно будет примерно сферическим , и с 2006 года классифицируется как карликовая планета, если оно вращается вокруг Солнца ( то есть, если это не спутник другой планеты). Меньшие тела, такие как астероиды , классифицируются как « маленькие тела Солнечной системы ».
Карликовая планета, по определению, недостаточно массивна, чтобы гравитационно очистить соседнюю область от планетезималей : не совсем известно, насколько большой должна быть планета, чтобы она могла эффективно очистить свои окрестности, но одной десятой массы Земли, безусловно, достаточно. .
Меньшие планеты содержат только силикаты и являются планетами земной группы, такими как Земля или Марс , хотя были обнаружены множественные суперземли с M E. Внутренняя структура каменистых планет зависит от массы: например, тектоника плит может потребовать минимальной массы для создания достаточных температур и давлений, чтобы это произошло.
Если протопланета вырастет за счет аккреции до более чем 5–10 M ⊕ , ее сила тяжести станет достаточно большой, чтобы удерживать водород в атмосфере . В этом случае он вырастет в газового гиганта . Если затем планета начнет миграцию , она может переместиться в пределах морозной линии своей системы и превратиться в горячий Юпитер, вращающийся очень близко к своей звезде, а затем постепенно теряя небольшое количество массы, поскольку излучение звезды разрушает ее атмосферу.
Теоретическая минимальная масса звезды может иметь, и до сих пор подвергаются водород сплав в ядре, по оценкам, составит около 75 M J , хотя слияние дейтерия может произойти в массах , как низко как 13 юпитеров.
Значения из эфемерид DE405
Эфемериды DE405 / LE405 из Лаборатории реактивного движения — это широко используемые эфемериды, датируемые 1998 годом и охватывающие всю Солнечную систему. Таким образом, массы планет образуют самосогласованный набор, что не всегда верно для более свежих данных (см. Ниже).
| Планеты и естественные спутники | Масса планеты (относительно Солнца × 10 −6 ) | Масса спутника (относительно родительской планеты) | Абсолютная масса | Средняя плотность | |
|---|---|---|---|---|---|
| Меркурий | 0. 166 01 | 3,301 × 10 23 кг | 5,43 г / см 3 | ||
| Венера | 2. 447 8383 | 4,867 × 10 24 кг | 5,24 г / см 3 | ||
| Система Земля / Луна | 3 040 432 633 33 | 6.046 × 10 24 кг | 4,4309 г / см 3 | ||
| земной шар | 3. 003 489 596 32 | 5,972 × 10 24 кг | 5,514 г / см 3 | ||
| Луна | 1. 230 003 83 × 10 −2 | 7.348 × 10 22 кг | 3,344 г / см 3 | ||
| Марс | 0,3227151 | 6,417 × 10 23 кг | 3,91 г / см 3 | ||
| Юпитер | 954,79194 | 1,899 × 10 27 кг | 1,24 г / см 3 | ||
| Ио | 4,70 × 10 −5 | 8,93 × 10 22 кг | |||
| Европа | 2,53 × 10 −5 | 4,80 × 10 22 кг | |||
| Ганимед | 7,80 × 10 −5 | 1,48 × 10 23 кг | |||
| Каллисто | 5,67 × 10 −5 | 1,08 × 10 23 кг | |||
| Сатурн | 285,8860 | 5,685 × 10 26 кг | 0,62 г / см 3 | ||
| Титан | 2,37 × 10 −4 | 1,35 × 10 23 кг | |||
| Уран | 43,66244 | 8,682 × 10 25 кг | 1,24 г / см 3 | ||
| Титания | 4,06 × 10 −5 | 3,52 × 10 21 кг | |||
| Оберон | 3,47 × 10 −5 | 3,01 × 10 21 кг | |||
| Нептун | 51,51389 | 1.024 × 10 26 кг | 1,61 г / см 3 | ||
| Тритон | 2,09 × 10 −4 | 2,14 × 10 22 кг | |||
| Карликовые планеты и астероиды | |||||
| Система Плутон / Харон | 0,007396 | 1,471 × 10 22 кг | 2,06 г / см 3 | ||
| Церера | 0,00047 | 9,3 × 10 20 кг | |||
| Веста | 0,00013 | 2,6 × 10 20 кг | |||
| Паллада | 0,00010 | 2,0 × 10 20 кг | |||
Масса Земли и лунная масса
Если у планеты есть естественные спутники, ее масса обычно указывается для всей системы (планета + спутники), так как это масса всей системы, которая действует как возмущение на орбитах других планет. Различие очень незначительное, поскольку естественные спутники намного меньше своих родительских планет (как видно из таблицы выше, где перечислены только самые большие спутники).
Примером могут служить Земля и Луна, отчасти потому, что Луна необычно велика (чуть более 1% массы Земли) по сравнению с ее родительской планетой по сравнению с другими естественными спутниками. Есть также очень точные данные, доступные для системы Земля – Луна, в частности, из эксперимента по лазерной дальнометрии Луны (LLR).
Геоцентрическая гравитационная постоянная — произведение массы времен Земли в ньютоновской гравитационной постоянной — может быть измерена с высокой точностью из орбит Луны и искусственных спутников. Отношение двух масс можно определить по небольшому колебанию орбиты Земли, вызванному гравитационным притяжением Луны.
Более свежие значения
Создание полных и высокоточных эфемерид Солнечной системы — непростая задача. Можно (и несколько проще) построить частичные эфемериды, которые касаются только интересующих планет (или карликовых планет, спутников, астероидов), «зафиксировав» движение других планет в модели. Эти два метода не являются строго эквивалентными, особенно когда дело доходит до определения неопределенностей результатов: однако «наилучшие» оценки — по крайней мере, с точки зрения указанных неопределенностей в результате — для масс малых планет и астероидов обычно получаются из частичных эфемериды.
Тем не менее, новые полные эфемериды продолжают готовиться, в первую очередь эфемериды EPM2004 от Института прикладной астрономии Российской академии наук . EPM2004 основан на 317 014 отдельных наблюдениях между 1913 и 2003 годами, что более чем в семь раз больше, чем DE405, и дал более точные массы Цереры и пяти астероидов.
| EPM2004 | Витальяно и Штосс (2006) | Браун и Шаллер (2007) | Толен и др. (2008) | Питьева и Стэндиш (2009) | Рагоззин и Браун (2009) |
|---|---|---|---|---|---|
| 136199 Эрис | 84,0 (1,0) × 10 −4 | ||||
| 134340 Плутон | 73,224 (15) × 10 −4 | ||||
| 136108 Хаумеа | 20,1 (2) × 10 −4 | ||||
| 1 Церера | 4,753 (7) × 10 −4 | 4,72 (3) × 10 −4 | |||
| 4 Веста | 1,344 (1) × 10 −4 | 1,35 (3) × 10 −4 | |||
| 2 Паллада | 1,027 (3) × 10 −4 | 1,03 (3) × 10 −4 | |||
| 15 Евномия | 0,164 (6) × 10 −4 | ||||
| 3 Юнона | 0,151 (3) × 10 −4 | ||||
| 7 Ирис | 0,063 (1) × 10 −4 | ||||
| 324 Бамберга | 0,055 (1) × 10 −4 |
Лучшие оценки IAU (2009 г.)
Новый набор «текущих наилучших оценок» различных астрономических констант был одобрен 27-й Генеральной ассамблеей Международного астрономического союза (МАС) в августе 2009 года.
| Планета | Отношение массы Солнца к массе планеты (включая спутники) | Масса планеты (относительно Солнца × 10 −6 ) | Масса (кг) | Ссылка |
|---|---|---|---|---|
| Меркурий | 6023,6 (3) × 10 3 | 0. 166 014 (8) | 3,30 · 10 (3) × 10 23 | |
| Венера | 408 523 719 (8) × 10 3 | 2 081 062 72 (3) | 4,1380 (4) × 10 24 | |
| Марс | 3098. 703 59 (2) × 10 3 | 0. 323 237 1722 (21) | 6,4273 (6) × 10 23 | |
| Юпитер | 1 047 3486 (17) × 10 3 | 954.7919 (15) | 1,89852 (19) × 10 27 | |
| Сатурн | 3. 497 9018 (1) × 10 3 | 285. 885 670 (8) | 5,6846 (6) × 10 26 | |
| Уран | 22. 902 98 (3) × 10 3 | 43. 662 44 (6) | 8,6819 (9) × 10 25 | |
| Нептун | 19. 412 26 (3) × 10 3 | 51. 513 84 (8) | 1,02431 (10) × 10 26 |
Текущие наилучшие оценки IAU (2012 г.)
Набор «текущих наилучших оценок» за 2009 год был обновлен в 2012 году резолюцией B2 XXVIII Генеральной Ассамблеи IAU. Улучшенные значения были даны для Меркурия и Урана (а также для системы Плутона и Весты).
Источник