Методы определения расстояний вселенной
Определение расстояний до планет.
Ср. расстояние r планеты от Солнца (в долях а.е.) находят по периоду ее обращения T:
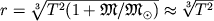
где r выражено в а.е., а T — в земных годах. Массой планеты 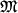
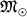
Определение расстояний до ближайших звезд.
Вследствие годичного движения Земли по орбите близкие звезды немного перемещаются относительно далеких «неподвижных» звезд. За год такая звезда описывает на небесной сфере малый эллипс, размеры к-рого тем меньше, чем дальше звезда. В угловой мере большая полуось этого эллипса приблизительно равна величине макс. угла, под каким со звезды видна 1 а.е. (большая полуось земной орбиты), перпендикулярная направлению на звезду. Этот угол (

Расстояние r до звезды, определяемое по величине ее тригонометрич. параллакса 
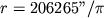
где параллакс 
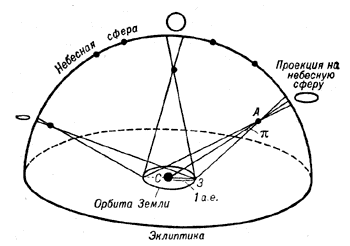 |
| Рис. 1. Определение расстояния до звезды А по ее видимому годичному перемещению на небесной сфере, вызванному движением Земли по орбите;  — параллакс — параллакс звезды А, С — Солнце, З — Земля, расстояние между ними равно 1 а.е. |
Для удобства определения расстояний до звезд с помощью параллаксов в астрономии применяют спец. единицу длины — парсек (пк). Звезда, находящаяся на расстоянии 1 пк, имеет параллакс, равный 1″. Согласно ф-ле (2), 1 пк=206265 а.е.= 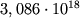
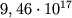
Ближайшая к Солнечной системе звезда — красный карлик 12-й звездной величины Проксима Кентавра — имеет параллакс 0,762, т.е. расстояние до нее равно 1,32 пк (4,3 св. года).
Нижний предел измерений тригонометрич. параллаксов
0,01″, поэтому с их помощью можно измерять расстояния, не превышающие 100 пк (с относит. погрешностью 50%). При расстояниях до 20 пк относит. погрешность не превышает 10%. Расстояния до более далеких звезд в астрономии определяют в основном фотометрич. методом (см. ниже).
Кроме параллактич. смещений близких звезд можно отметить лишь два случая, когда видимые перемещения деталей космич. объектов по небу можно также использовать для точного определения расстояний до них. Это — неск. движущихся близких звездных скоплений и быстро перемещающиеся газовые оболочки или сгущения. Примером явл. новые и сверхновые звезды, для разлетающихся оболочек к-рых наряду с видимой скоростью расширения в угловых секундах можно определить спектр. способом радиальную скорость расширения.
Фотометрический метод определения расстояний.
Освещенности, создаваемые одинаковыми по мощности исчтониками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m — видимая, M — абсолютная звездная величина) приводит к следующей осн. ф-ле фотометрич. расстояний rф (пк):
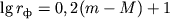
Для светил, у к-рых известны тригонометрич. параллаксы, можно, определив M по этой же ф-ле, сопоставить физ. св-ва с абс. звездными величинами. Это сопоставление показало, что абс. звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физ. св-в.
Осн. способом оценки абс. величин звезд явл. спектральный: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абс. величины (чаще всего это усиление линий ионизов. атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости (см. Светимости классы ). По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абс. величины с погрешность до 0,5 m . Эта погрешность соответствует относительной погрешности 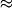
Для определения расстояний до звездных скоплений имеется спец. способ, использующий диаграмму «видимая величина-показать цвета» звезд скопления. Она сравнивается с диаграммой «абс. величина-показать цвета», к-рая составлена по звездам того же типа близких к нам скоплений (рис. 2). Сдвиг между сравниваемыми диаграммами по вертикали равен модулю расстояния (m-M), по к-рому при помощи ф-лы (3) и находят т.н. фотометрич. расстояние rф звездного скопления (с относительной погрешностью 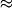
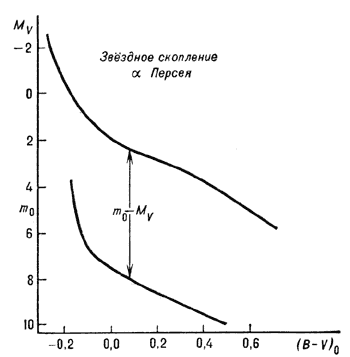 |
| Рис. 2. Зависимость «абсолютная звездная величина MV-показатель цвета (B-V)0» для исходной главной последовательности (верхняя кривая) и зависимость «видимая звездная величина m0 — показатель цвета» скопления 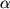 Персея (нижняя кривая); m0 — Персея (нижняя кривая); m0 — видимая звездная величина, свободная от межзвездного поглощения света. Сдвиг по оси звездных величин равен модулю расстояний m0—MV. |
Важный метод определения фотометрич. расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном св-ве переменных звезд — цефеид . Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абс. величину +0,5 m . Они встречаются в шаровых звездных скоплениях, в центр. области и сферич. короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.
Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно к-рой, чем короче период колебаний блеска, тем цефеида слабее по абс. величине. С помощью этой зависимости можно определить абс. величины цефеид по длительности их периодов колебаний блеска и, следовательно,фотометрич. расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость ). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).
Определение внегалактических расстояний.
Расстояния до ближайших галактик были установлены по оценкам видимых звездных величин цефеид и ярчайших звезд в этих звездных системах. Более тысячи цефеид найдено в Магеллановых Облаках , неск. сотен — в Туманности Андромеды. Цефеиды обнаруженф также в семи неправильных и спиральных галактиках, находящихся в радиусе ок. 3 Мпк вокруг нашей Галактики.
В системах, где не удается обнаружить цефеиды, ищут ярчайшие звезды-сверхгиганты и гиганты высших классов светимости. Ярчайшие сверхгиганты обнаружены в неск. сотнях спиральных и неправильных галактик в радиусе до 10 Мпк (абс. величины их — от -9 до -10 m ). В эллиптич. галактиках население I типа (долгопериодич. цефеиды, сверхгиганты и горячие газовые туманности) отсутствует. Оданко небольшие эллиптич. галактики нашей Местной группы (см. Галактики ) на фотографиях распадаются назвезды, ярчайшие из к-рых оказались красными гигантами, аналогичными гигантам в шаровых звездных скоплениях нашей Галактики (абс. величины этих гигантов достигают -2 m , радиус обнаружения — ок. 1 Мпк). По красным гигантам удается оценивать фотометрич. расстояния до эллиптич. галактик внутри Местной группы галактик с погрешностью 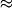
В качестве индикаторов расстояний используются также новые звезды и сверхновые звезды .
В нек-рых галактиках наблюдаются яркие газовые туманности. Оказалось, что линейные размеры наибольших туманностей в галактиках почти одинаковы. Поэтому, измерив угловые размеры d» ярчайшей туманности в к.-л. галактике, можно определить расстояние r до этой галактики. Данный способ применим к спиральным и неправильным галактикам до расстояний 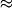
До остальных галактик фотометрич. расстояния можно определять более грубым способом по оценке интегральной звездной величины галактики. По особенностям внеш. вида спиральных галактик (толщина, длина спиральных рукавов, поверхностная яркость и т.п.) часто можно грубо оценить светимость галактики или, по крайней мере, установить, что галактика не относится к числу карликовых. В последнем случае ее абс. интегральную величину можно условно принять равной -20 m (ср. значение для галактик-гигантов) и по видимой величине грубо оценить расстояние.
На больших расстояниях (> 1000 Мпк) видимый блеск галактик и др. космич. объектов ослабляется не только в силу фотометрического закона квадрата расстояния, но также, помимо поглощения света, вследствие красного смещения — «покраснения» далеких источников излучения, отражающего расширение Вселенной, что приходится учитывать при определении фотометрич. расстояний.
Определение расстояний по красному смещению
Сравнение фотометрич. расстояний до галактик с величиной смещения z их спектр. линий к красному концу спектра показало, что величина 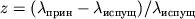
r=cz/H (Мпк). (4)
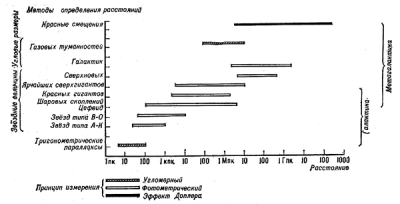 |
| Рис. 3. Методы определения расстояний до звезд и внегалактических объектов; указаны современные пределы применимости методов и основные измерительные принципы. |
В пределах систем галактик (пар, групп, скоплений) эта зависимость неприменима из-за собст. скоростей галактик в этих системах. Определение расстояний до сравнительно близких галактик по ф-ле (4) требует также учета движения нашей Галактики в Местной группе галактик и Местной группы относительно окружающих галактик (эта скорость составляет неск. сотен км/с). Проверка пропорциональности красного смещения фотометрич. расстоянию для галактик и радиогалактик, предельно доступных наблюдениям в телескопы, в основном подтвердила закон Хаббла. Однако расстояние, определенное по красному смещению (хаббловское), уже нельзя считать фотометрическим, хотя H и получена по фотометрическим расстояниям галактик.
До 500 Мпк система внегалактич. расстояний (фотометрич. и хаббловских) проверена прямыми определениями расстояний до сверхновых звезд по измерениям их поверхностных темп-р и скоростей расширения оболочек. Надежных оценок значительно больших расстояний пока нет.
На рис. 3 показаны пределы применимости расмотренных методов определения расстояний до космич. объектов.
Для галактик с z>0,5 зависимость (4) принимает более сложный вид и неодинакова для различных космологич. моделей Вселенной.
Лит.:
Струве О., Линдс Б., Пилланс Э., Элементарная астрономия, пер. с англ., М., 1967; Агекян Т.А., Звезды, галактики, метагалактика, 2 изд., М., 1970; Ефремов Ю.Н., В глубины Вселенной, 2 изд., М., 1977; Воронцов-Вельяминов Б.А., Внегалактическая астрономия, 2 изд., М., 1978.
Источник
Как измеряют расстояния во Вселенной?
Как астрономы узнают расстояния до космических объектов?
Ответ
Для определения расстояний в космосе используют около двадцати методов, сменяющих один другой по мере перехода ко всё более удалённым объектам. Мы рассмотрим основные методы.
1. Исторически самым первым способом измерения расстояний до космических тел был метод, который уже давно применялся для измерения расстояний до недоступных объектов на поверхности Земли — метод тригонометрического параллакса. Заключается он в том, что измеряется расстояние между двумя точками на земной поверхности. Полученный отрезок называется базисом. На нём, как на основании (базис), строится треугольник, третьей вершиной которого является тот недоступный объект, расстояние до которого нам нужно узнать. С помощью угломерного инструмента измеряются два угла треугольника при базисе. Если известны сторона и два прилежащих угла треугольника, то, как мы помним из школьного курса геометрии (тема «Решение треугольников»), можно найти все остальные элементы треугольника. Таким образом можно определить расстояние до недоступного объекта.
Наши два глаза при оценке расстояний работают точно так же: два луча зрения на предмет образуют угол, который тем меньше, чем дальше расположен рассматриваемый объект. При рассматривании близких объектов глаза больше скошены, а при рассматривании очень далёких объектов глаза смотрят почти параллельно. Если поочерёдно закрывать глаза, то положение рассматриваемого объекта будет смещаться на фоне более далёких объектов. Чем ближе объект, тем смещение больше, чем дальше — тем меньше. Так как расстояния до космических объектов очень большие, то угол, называемый параллаксом (угол, под которым с далёкого объекта виден базис), будет очень маленьким. Чтобы его увеличить, нужно взять базис как можно больше. Для измерения расстояний до планет Солнечной системы за базис берут радиус Земли. Угол, под которым с небесного тела виден радиус Земли, перпендикулярный лучу зрения, называется горизонтальным параллаксом. Для близких звёзд за базис берут средний радиус орбиты Земли (астрономическая единица) и параллакс называется годичным параллаксом, он составляет всего лишь доли секунды (градус делится на 60 угловых минут, а минута на 60 угловых секунд). Если годичный параллакс некоторой звезды равен 1 секунде (то есть радиус земной орбиты виден с неё под углом, равным 1 секунде), то такое расстояние называется парсеком. До ближайшей звезды Проксима Центавра чуть больше одного парсека или 4,22 светового года. Таким методом с Земли можно измерить расстояния вплоть до 100 парсеков.
С помощью внеатмосферных наблюдений со спутников (спутник HIPPARCOS/Гиппарх, запущенный в 1989 году) можно измерить углы до 0.001″, что соответствует расстоянию в 1000 парсеков. В 2013 году был запущен спутник Gaia/Гея, который способен измерять параллаксы с точностью ещё в сто раз большей, что позволит определить расстояния до миллиарда звёзд нашей галактики (0,5% всех звёзд Галактики) на расстоянии до 40000 парсеков. Для более далёких звёзд метод параллакса не работает, т. к. невозможно измерить ещё более малые параллаксы, величина их много меньше точности измерительных приборов.
2. Методы радиолокации и лазерной локации. На космический объект с помощью радиопередатчика посылается мощный узконаправленный радиосигнал в виде кратковременного импульса. После отражения космическим объектом сигнал в ослабленном виде возвращается на Землю и принимается приёмником. По величине запаздывания вычисляется расстояние до объекта. Таким методом измеряются расстояния в Солнечной системе (Меркурий, Венера, Марс, Сатурн и Юпитер со спутниками, астероиды, кометы, корона Солнца) с точностью до нескольких километров. Для дальних планет метод не работает, т. к. сигнал сильно рассеивается (энергия принятого радиоэха обратно-пропорциональна четвёртой степени расстояния), трудно получить достаточно узко направленный пучок радиоволн, нужны очень мощные передатчики, огромные антенны и сверхчувствительные приёмники. Для Луны осуществлена лазерная локация, для этого на неё были доставлены оптические отражатели. Точность лазерной локации составляет 1 см.
3. Метод стандартной свечи. Мы знаем, что освещённость, создаваемая источником света, убывает обратно пропорционально квадрату расстояния до него (если лампочку отодвинуть в два раза дальше от стены, то освещённость стены уменьшится в 4 раза, если удалить в три раза, то освещённость уменьшится в девять раз и т. д.).
Чем меньше приходит на Землю света от звезды, тем, значит, она дальше. Если известна мощность источника света (в астрономии это светимость звезды), то по величине освещённости (в астрономии — видимый блеск звезды) можно вычислить расстояние до него по закону обратных квадратов. Например, мы хорошо знаем светимость Солнца. Если мы обнаружим такую же по физическим характеристикам звезду, как наше Солнце, то по её видимой звёздной величине (освещённости, создаваемой ею на Земле) мы легко вычислим расстояние до неё — звезда во столько раз находится дальше, чем Солнце, во сколько раз в квадрате её яркость меньше яркости Солнца. За стандартную свечу, кроме Солнца, можно брать любую другую звезду, расстояние до которой ранее измерено методом тригонометрического параллакса.
3′. Метод цефеид. За стандартную свечу можно взять цефеиду — пульсирующую звезду. Светимость и, соответственно, видимый блеск цефеиды периодически меняется. Известен закон, связывающий светимость цефеиды и период её пульсаций. Период и видимый блеск цефеид легко измерить, а отсюда легко вычислить и расстояние до неё. Цефеиды называют «маяками Вселенной». Если в какой-либо галактике обнаружена цефеида, то мы, вычислив расстояние до цефеиды, тем самым находим и расстояние до этой галактики.
3». Метод сверхновых. Точно так же за стандартную свечу можно взять некоторые типы сверхновых звёзд, то есть взрывающихся звёзд. Известно, сколько энергии выделяет сверхновая при взрыве. Сравнивая видимый блеск сверхновой с её истинной светимостью, мы определяем, на каком расстоянии от нас она находится, а, соответственно, и той далёкой галактики, которой она принадлежит.
Источник