Измерить расстояние Земля-Луна с помощью лазера сложнее, чем вы думаете
Как измерить расстояние Земля-Луна? Какие результаты измерений и зачем их вообще делать? Вот ответы на эти интересные вопросы.
Одним из аргументов, используемых для опровержения теории о ложной посадке на наш естественный спутник, является информация об измерении расстояния Земля-Луна лазерным лучом. Для сторонников теории заговора нет таких свидетельств, как фотогалерея Аполлона, но научное значение измерений очень важно.
Напомним, первые геометрические попытки оценить расстояние Земля-Луна, хотя и ошибочные из-за несовершенства методов измерения, были предприняты Аристархом Самосским более 2000 лет назад.
Но вернемся в наше время. Лазерный луч излучается в специальные световозвращатели, оставленные на Луне миссиями Аполлон 11 , 14 и 15, а также Луноходами 1 и 2, установленными на советских луноходах. Благодаря этим измерениям мы знаем, например, что наш космический спутник удаляется от Земли со скоростью примерно 3,8 сантиметра в год. За это ответственны приливные силы, те же силы, которые вызывают приливы и отливы в земных морях и океанах.
Чем дальше Луна от Земли, тем длиннее наш день
За время жизни одного человека Луна удалится на 3 метра от Земли. Это немного. Когда мы начнем накапливать эти знания, они станут более важными. С началом эпохи великих географических открытий расстояние увеличилось на 20 метров. С момента появления на Земле первых гоминидов прошло 152 километра. Конечно, мы говорим о среднем расстоянии Земля-Луна, потому что из-за эллиптической орбиты мгновенное расстояние от Земли до Луны изменяется примерно на 50 000 километров в течение месяца. В настоящее время это в среднем 386 тысяч километров.
Изменение расстояния также влияет на Землю. Чем дальше находится Луна, тем медленнее Земля вращается вокруг своей оси. Продолжительность земного дня увеличивается. Конечно, в ходе человеческой жизни и даже существования нашей цивилизации изменения очень незначительны. За столетие день увеличивается всего на 2 миллисекунды. Это изменение не следует путать с расхождениями, возникающими в результате измерения времени с использованием атомных и астрономических часов — оно является результатом дополнительной секунды и не связано с замедлением скорости вращения Земли вокруг своей оси.
Мы не можем рассчитывать на 25 часов в нашей жизни. Есть модели, которые предполагают, что около 1,4 миллиарда лет назад, когда жизнь на Земле достигала уровня отдельных клеток, сутки длились 18 часов. Они также показывают, что темпы удаления изменчивы, поэтому трудно экстраполировать 3,8 сантиметра в год на геологическую шкалу времени.
Измерения расстояний и внутреннее строение Луны
Изменения продолжительности земных суток — не единственное ценное заключение, которое следует из измерений расстояний. Сегодня мы знаем, что у Луны, скорее всего, жидкое ядро. Теперь цель исследования — уточнить результаты и ответить на вопрос, является ли внутренняя часть ядра твердой, как Земля. Вся эта информация окажется бесценной для отслеживания истории лунного магнитного поля. Оно когда-то существовало и было сильным, а сегодня находится в зачаточном состоянии.
Как работает измерение расстояния Земля-Луна?
Самая большая светоотражающая панель, которую оставили позади астронавты Аполлона-15, имеет размеры 105 х 65 сантиметров. Это не плоское зеркало, а поверхность, покрытая угловыми отражателями, используемыми в лазерных измерениях (первые два имеют 100 таких отражателей, третье 300). Одиночные такие рефлекторы также размещаются на марсоходах, но они используются только для измерений с орбиты Марса.
Они работают так, что независимо от направления, с которого свет падает на панель, наблюдатели имеют гарантию, что он будет отражен обратно в направлении, параллельном направлению прихода. В случае обычного зеркала только свет, падающий прямо перед собой, мог бы вернуться к наблюдателю, и такое точное размещение объекта на поверхности Луны относительно передатчика на Земле было бы чудом.
В направлении зеркал излучается лазерный луч, который после отражения возвращается на Землю и регистрируется. Измеряется задержка, оценивается расстояние.
Почему все кажется простым, а на самом деле это не так?
В настоящее время измерения расстояния от Земли до Луны производятся с точностью до одного миллиметра. Сигнал, отправленный на Луну, отраженный от рефлектора, возвращается на Землю через 2,5 секунды. Возвращается, но не всегда! И неудивительно, ведь все это измерение расстояний очень сложно.
Первая проблема — это когерентность пучка. Относительно сфокусированный лазерный луч, который даже на Земле довольно большой, потому что он должен быть достаточно сильным, чтобы проникнуть в атмосферу Земли (дважды), на расстоянии Луны он даже 2 километра в ширину. Если его можно будет направить на отражатель, несколько фотонов в луче попадут в него, и еще меньше, вероятно, будет зарегистрировано обратно на Землю.
По данным НАСА, вероятность того, что одиночный фотон, излучаемый с Земли в направлении отражателя, оставленного Аполлоном 11. Вероятность того, что каждый из этих счастливых фотонов вернется на Землю и будет зарегистрирован, составляет 1/25 000 000, составляет 1/25 000 000. .
Поэтому, хотя измерения проводятся регулярно, это сложная задача. Есть еще одна проблема. На Земле принимается только 1/10 ожидаемого сигнала обратной связи. Предполагается, что панели каким-то образом загрязнились. Кажется, что на Луне сложно найти пыльную бурю, ведь ее атмосфера похожа на лучший вакуум, когда-либо созданный на Земле. Действительно, пыльной бури масштаба Марса не будет. Однако пыль, поднятая с поверхности, например, падающими метеороидами, даже на Луне может быть проблемой. Сделан первый шаг к прояснению трудностей измерения. Поэтому НАСА в сотрудничестве с французскими учеными решило использовать рефлектор на лунном рекоассансном орбитальном аппарате (LRO), чтобы выяснить суть проблемы. Этот отражатель размером с небольшую книгу, сам орбитальный аппарат все еще находится в движении, поэтому задача огромна. В итоге, однако, удалось зарегистрировать сигнал обратной связи после многих попыток. Чтобы повысить точность измерения, во французском центре в Грассе вместо зеленого лазерного луча использовались менее чувствительные инфракрасные и импульсные лазеры.
Сегодня известно, что что-то не так с ретрорефлекторами, отражающими лазерные лучи на Луне. И ученые прилагают максимум сил, чтобы точно определить, что на самом деле является причиной этих проблем.
Источник
Лазерная локация Луны
Содержание
Общие принципы лазерной локации
Едва только был изобретён лазер, так сразу же возникла идея попробовать его применить для цели точного измерения расстояния до Луны. [1] Для этого короткий импульс излучения лазера направляется в сторону Луны, и измеряется интервал времени между излучением лазерного пучка и приёмом отражённого сигнала, а расстояние вычисляется исходя из постоянства скорости света в вакууме и учёта задержки распространения сигнала в атмосфере [2] . Этому способствует малая расходимость лазерного пучка, обеспечивающая высокую интенсивность освещения цели, монохроматичность, позволяющая выделить слабый полезный сигнал на фоне засветки при помощи узкополосного спектрального фильтра, а также малая длительность импульса, позволяющая выполнять измерение расстояния с высокой точностью (т.е. с малой погрешностью, прямо пропорциональной длительности импульса). Советские учёные получили отражённый лазерный сигнал с Луны и измерили до неё расстояние аж в 1966 году до всех лунных похождений НАСА [3] [4]
Теоретические расчёты
Энергия одного фотона Eφ однозначно определяется его частотой ν. 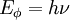
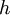
| Тип лазера | Длина волны λ(нм) | Цвет | Частота ν(ТГц) | Энергия фотона Eφ(Дж) |
|---|---|---|---|---|
| Рубин | 694,3 | красный | 299,8 | 2,86•10 -19 |
| Неодимовый | 1064 | инфракрасный | 281,8 | 1,87•10 -19 |
| Неодимовый с удвоением частоты | 532 | зелёный | 563,5 | 3,73•10 -19 |
Частота и длина волны света в вакууме однозначно связаны друг с другом и скоростью света в вакууме 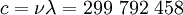
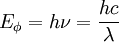
Количество фотонов Nt, испускаемых в импульсе, легко подсчитать, зная энергию импульса лазера W. 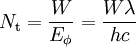
Испускаемый лазерный луч должен быть как можно лучше сколлимирован — чем меньше расходимость, тем лучше. Наилучшая реально достижимая расходимость — примерно 1 угловая секунда. Она складывается из дифракционного расширения луча, обусловленного диаметром выходного луча 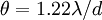
Пока луч будет преодолевать атмосферу, он частично поглотится, частично рассеется, частично пройдёт. Для обсерваторий указывается средний коэффициент прозрачности атмосферы Кα — для Крымской астрофизической обсерватории, к примеру, он равен 73%. Аналогичное поглощение и рассеяние произойдёт в атмосфере при возвращении пучка фотонов. Количество фотонов NM, которые достигнут Луны, равно 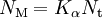
Среднее расстояние между центрами Луны и Земли R принимается равным 384 467 км, перигей 363 104 км, апогей 405 696 км.
Луч, имеющий расхождение θ 1 угловая секунда, на Луне осветит пятно диаметром D примерно 1,9 км, при большей расходимости диаметр пятна пропорционально увеличивается. При малых углах можно пользоваться приближением 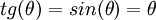
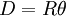
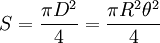
Если луч попал на УО, то основная часть фотонов, попавших на него, будет отражена назад. При этом несколько увеличится расхождение пучка, скажем, УО французского изготовления, установленные на «Луноходах», дают рассеяние пучка θ’ на 6 угловых секунд. Площадь УО S0, установленных на «Луноходах» составляет 0.064 м 2 . Площадь УО, якобы доставленных экспедициями «Аполлон-11» и «Аполлон-14» составляет 0.1134 м 2 , «Аполлон-15» — 0.34 м 2 . Количество фотонов N0, отражённых от УО, равно 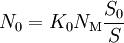
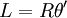
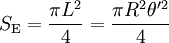
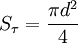
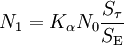
Если луч попал на грунт, то он преимущественно поглотится, а отражённая часть рассеется по закону, близкому к ламбертовскому (равномерное рассеяние во все стороны). Отличие лунного грунта от других поверхностей заключается в том, что у лунного грунта имеются ярко выраженные эффекты обратного рассеяния и оппозиционный эффект — количество света, отражаемого строго в обратном направлении, в 2-3 раза больше чем для обычной ламбертовской поверхности. [6] Поскольку нас интересует отражение только строго назад, то мы можем подсчитать как для ламбертовского рассеяния, умножив результат на коэффициент k≈2,5, включающий в себя обратное рассеяние и оппозиционный эффект. Среднее альбедо Луны A принимается равным 7%, хотя для разных участков лунной поверхности оно варьируется от 5% до 17%. [6]
Пятно на грунте, освещаемое лазером, достаточно маленькое — оно всё целиком помещается в поле зрения телескопа, которое определяется предельным увеличением, которое определяется диаметром телескопа. Скажем, для телескопа КрАО диаметром 2.64 м поле зрения составляет 15 угловых секунд [7] . Соответственно, количество фотонов, попадающих в телескоп при отражении от грунта, равно 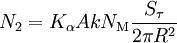
Исходя из этих расчётов можно вывести формулу для оценки эффективности применения уголкового отражателя 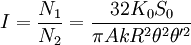
В работе [7] формула для отражения от УО дана в таком виде: 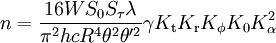
Далеко не все фотоны, попавшие в телескоп, будут зарегистрированы. Для начала они пройдут через пространственный фильтр и узкополосный спектральный фильтр. Коэффициент пропускания спектрального фильтра на рабочей длине волны равен примерно 40%.
Фотоны, прошедшие через фильтр, попадают на фотопреобразователь — либо фотоэлектронный умножитель (ФЭУ), либо фотодиод (лавинный фотодиод) или даже матрицу фотодиодов. ФЭУ-77, использовавшийся в КрАО, имел квантовый выход Кφ 0.09 [5] [7] . Современные лавинные фотодиоды имеют квантовый выход 0,3 [11] . Новейшие разработки в этой области — сверхпроводящие детекторы единичных фотонов (SSPD) имеют квантовый выход 0.67 (на длине волны 1064 нм) при очень низком джиттере (50 ps) и низком уровне собственных шумов [12] , но ещё не было публикаций об использовании детекторов такого типа при лазерной локации Луны.
Сигнал с фотопреобразователя подвергается фильтрации для снижения шума. В первых экспериментах по лазерной локации ставились 2 фотопреобразователя, выходы которых объединялись через логическую схему совпадения по «И» — сигнал засчитывался, если оба фотопреобразователя одновременно принимают фотоны. [13] В современных системах используется временной фильтр, пропускающий сигнал только во время короткого окна пропускания длительностью 500 нс. [9] [14]
Уголковые отражатели
Повышение точности измерений при помощи импульсной лазерной локации возможно в случае применения уголковых отражателей (УО). УО представляет собой три отражающие плоскости, взаимно пересекающиеся под прямым углом. В радиодиапазоне плоскости выполняются просто из металлических пластин («hollow cube», «пустой куб»). В оптическом диапазоне отражающие плоскости формируются на гранях куба, изготовленного из прозрачного материала (кварцевое стекло). Дополнительно улучшить коэффициент отражения можно путём вакуумного напыления металлического слоя (серебро, алюминий) на грани УО. Если углы между гранями выполнены с достаточно высокой точностью, то уголковый отражатель всегда отражает излучение строго в обратном направлении независимо от направления, откуда падает луч на УО, во всём рабочем диапазоне углов.
По расчётам применение УО на Луне позволяет на 1-2 порядка усилить отражённый сигнал, принимаемый на Земле, по сравнению с отражением от грунта, и сделать его компактным во времени, в отличие от сигнала, отражающегося от грунта, поэтому размазанного во времени из-за рельефа местности. [15]
Французский уголковый отражатель, установленный на «Луноходах», был составлен из триппель-призм с ребром 12 см и имел расходимость отражённого пучка примерно 6″ (для света рубинового лазера с длиной волны 694,3 нм). Грани триппель-призм были покрыты серебром, это увеличивало коэффициент отражения до 0.9, но из-за разного коэффициента теплового расширения серебра и кварца приводило к деформации призм при нагреве лунным днём и, как следствие, к ухудшению отклика. Активная площадь УО составляла 640 см 2 . Рабочий диапазон составлял ±10 градусов от нормали. [5]
Американские уголковые отражатели, якобы доставленные на Луну, были составлены из призм диаметром 3.8 см и имели расходимость отражённого пучка примерно 8,6″ (для 694,3 нм). Грани триппель-призм не были покрыты металлом, это уменьшало термические деформации, но ухудщало коэффициент отражения УО до 0.27. Активная площадь УО «Аполлон-11» и «Аполлон-14» составляла 0,1134 м 2 (100 триппель-призм), «Аполлон-15» 0,34 м 2 (300 триппель-призм). Триппель-призмы были глубоко утоплены в своих индивидуальных гнёздах, что дополнительно ухудшало видимость триппель-призм при отклонении от нормали и приводило к снижению отклика на 5% при отклонении на каждый градус от нормали. [15] [13]
Расходимость отражённого пучка зависит от точности изготовления призм уголкового отражателя и их апертуры DR, которая обусловливает дифракционную расходимость 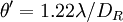
Иногда в статьях по локации используют понятие эффективной площади рассеяния (ЭПР). Она имеет размерность в м 2 , но не означает действительную площадь. Эта характеристика включает в себя не только геометрическую площадь отражателя, но и коэффициент отражения, расходимость отражённого пучка и т.д. Эффективная площадь рассеяния зависит не только от характеристик самого отражателя, но и от угла падения (отклонение вектора падающего на отражатель пучка от нормали), а также длины волны, которая влияет на дифракционное расширение отражённого пучка. Для уголкового отражателя существует предельный угол падения. При отклонении луча от нормали сверх предельного угла отражатель не может функционировать. Для «пустого куба» предельный угол составляет примерно 30º, для кварцевой призмы предельный угол составляет примерно 45º [17]
Источник
