Журнал «Все о Космосе»
Астрономическая единица
Расстояние в а.е.
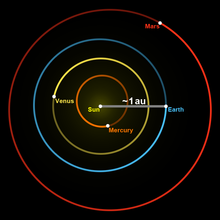
Астрономическая единица (русское обозначение: а. е.; международное: au) — исторически сложившаяся единица измерения расстояний в астрономии, приблизительно равная среднему расстоянию от Земли до Солнца.
Свет проходит это расстояние примерно за 500 секунд (8 минут 20 секунд).
Применяется в основном для измерения расстояний между объектами Солнечной системы, внесолнечных систем, а также между компонентами двойных звёзд.
В сентябре 2012 года 28-я Генеральная ассамблея Международного астрономического союза в Пекине приняла решение привязать астрономическую единицу к Международной системе единиц (СИ). Астрономическая единица по определению равна в точности 149 597 870 700 метрам. Кроме того, МАС принял решение стандартизовать международное обозначение астрономической единицы: «au». Иногда применяются также обозначения «a. u.» или «AU». Существует также международный стандарт ISO 80000-3, который рекомендует применять обозначение «ua».
В Российской Федерации астрономическая единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «астрономия». В соответствии с ГОСТ 8.417—2002, наименование и обозначение астрономической единицы не допускается применять с дольными и кратными приставками СИ.
Предыдущие определения
В соответствии с решением 10-й генеральной Ассамблеи МАС 1976 года астрономическая единица была определена как радиус круговой орбиты пробного тела в изотропных координатах, угловая скорость обращения по которой, при пренебрежении всеми телами Солнечной системы кроме Солнца, была бы точно равна 0,017 202 098 95 радиан в эфемеридные сутки. В системе постоянных IERS 2003 астрономическая единица полагалась равной 149 597 870,691 км.
История
Со времён появления гелиоцентрической системы, а особенно кеплеровской небесной механики, относительные расстояния в Солнечной системе (исключая слишком близкую Луну) стали известны с хорошей точностью. Поскольку Солнце является центральным телом системы, а обращающаяся по почти круговой орбите Земля — местоположением наблюдателей, естественно было принять радиус этой орбиты за единицу измерения. Однако не существовало способа надёжно измерить величину этой единицы, то есть сравнить её с земными масштабами. Солнце находится слишком далеко, чтобы с Земли надёжно измерить параллакс. Расстояние до Луны было известно, но исходя из известных в XVII веке данных оценить отношение расстояний до Солнца и Луны не удавалось — наблюдение за Луной не даёт требуемой точности, а отношение масс Земли и Солнца также не было известно.
В 1672 году Джованни Кассини совместно со своим сотрудником Жаном Рише измерили параллакс Марса. Поскольку параметры орбиты Земли и Марса были измерены с высокой точностью, появилась возможность оценить величину астрономической единицы — в современных единицах у них получилось примерно 140 млн км. Впоследствии проводились уточнённые измерения астрономической единицы при помощи прохождений Венеры по солнечному диску. Сближение астероида Эрос с Землёй в 1901 году и измерение его параллакса позволили получить ещё более точную оценку.
Астрономическая единица также уточнялась с помощью радиолокации планет. Локацией Венеры в 1961 году установлено, что астрономическая единица равна 149 599 300 км. Возможная ошибка не превышала 2000 км. Повторная радиолокация Венеры в 1962 году позволила уменьшить эту неопределенность и уточнить значение астрономической единицы: оно оказалось равным 149 598 100±750 км. Выяснилось, что до локации 1961 года величина а. е. была известна с точностью 0,1 %.
Многолетние измерения расстояния от Земли до Солнца зафиксировали его медленное увеличение со скоростью около 15 метров за сто лет (что на порядок превышает точность современных измерений). Одной из причин может быть потеря Солнцем массы (вследствие солнечного ветра), однако наблюдаемый эффект значительно превышает расчётные значения.
Источник
Астрономическая единица — Astronomical unit
| Астрономическая единица | |
|---|---|
 | |
| Основная информация | |
| Система единиц | Астрономическая система единиц (принята для использования с СИ) |
| Единица | длина |
| Символ | au или AU или AU |
| Конверсии | |
| 1 у.е. или AU или AU в . | . равно . |
| метрические ( СИ ) единицы | 1,495 978 707 × 10 11 м |
| имперские и американские единицы | 9.2956 × 10 7 миль |
| астрономические единицы | 4.8481 × 10 −6 шт. 1,5813 × 10 -5 LY |
Астрономическая единица (символ: АС или АС или АС ) является единицей длиной , примерно расстояние от Земли до Солнца и равна приблизительно 150 миллионов километров (93 миллиона миль) или \ 8 световых минут. Фактическое расстояние изменяется примерно на 3% по мере того, как Земля вращается вокруг Солнца, от максимума ( афелий ) до минимума ( перигелий ) и обратно один раз в год. Астрономическая единица изначально задумывалась как среднее значение афелия и перигелия Земли; однако с 2012 г. он определяется как 149 597 870 700 м .
Астрономическая единица используется в основном для измерения расстояний в Солнечной системе или вокруг других звезд. Это также фундаментальный компонент в определении другой единицы астрономической длины, парсек .
СОДЕРЖАНИЕ
История использования символа
Для обозначения астрономических единиц использовалось множество символов единиц и сокращений. В резолюции 1976 года Международный астрономический союз (МАС) использовал символ А для обозначения длины, равной астрономической единице. В астрономической литературе символ AU был (и остается) обычным явлением. В 2006 году Международное бюро мер и весов (BIPM) рекомендовало ua в качестве обозначения единицы. В ненормативном приложении C к ISO 80000-3 : 2006 (в настоящее время снято) символ астрономической единицы — «ua».
В 2012 году МАС, отметив, что «в настоящее время используются различные символы для астрономической единицы», рекомендовал использовать символ «au». В научных журналах , изданные Американского астрономического общества и Королевского астрономического общества впоследствии был принят этот символ. В Брошюре SI в редакции 2014 г. и в редакции 2019 г. BIPM использовал символ единицы измерения «au». ISO 80000-3: 2019, который заменяет ISO 80000-3: 2006, не упоминает астрономическую единицу.
Разработка определения единицы измерения
Орбита Земли вокруг Солнца представляет собой эллипс . Большая полуось этой эллиптической орбите определяется как половина прямой отрезка , соединяющего Афелий . Центр Солнца находится на этом отрезке прямой, но не в его середине. Поскольку эллипсы — это хорошо изученные формы, измерение точек их крайних точек определило точную форму математически и сделало возможными вычисления для всей орбиты, а также прогнозы, основанные на наблюдениях. Кроме того, он нанес на карту самое большое прямолинейное расстояние, которое Земля проходит в течение года, определив время и места для наблюдения самого большого параллакса (видимые сдвиги положения) у ближайших звезд. Знание смещения Земли и звезды позволило рассчитать расстояние до звезды. Но все измерения подвержены некоторой степени погрешности или неопределенности, а неопределенности в длине астрономической единицы только увеличивают неопределенности в звездных расстояниях. Повышение точности всегда было ключом к улучшению понимания астрономии. На протяжении двадцатого века, измерения становились все более точными и сложными, и все в большей степени зависит от точного наблюдения эффектов , описанных Эйнштейна «с теорией относительности и на математических инструментов он использовал.
Улучшение измерений постоянно проверялось и перекрестно проверялось посредством лучшего понимания законов небесной механики , которые управляют движением объектов в космосе. Ожидаемые положения и расстояния до объектов в установленное время вычисляются (в а.е. ) на основе этих законов и собираются в набор данных, называемый эфемеридами . НАСА «s Jet Propulsion Laboratory ГОРИЗОНТЫ Система обеспечивает один из нескольких услуг эфемерид вычислений.
В 1976 году, чтобы установить даже точную меру астрономической единицы, МАС официально принял новое определение . Хотя это определение было напрямую основано на лучших на тот момент наблюдательных измерениях, оно было переработано с точки зрения лучших на тот момент математических выводов из небесной механики и планетарных эфемерид. В нем говорилось, что «астрономической единицей длины является та длина ( A ), для которой гауссова гравитационная постоянная ( k ) принимает значение 0,017 202 098 95, когда единицами измерения являются астрономические единицы длины, массы и времени «. Эквивалентно, согласно этому определению, одна а.е. — это» радиус невозмущенной круговой ньютоновской орбиты вокруг Солнца частицы, имеющей бесконечно малую массу, движущуюся с угловой частотой от 0,017 202 098 95 радиан в сутки «; или, альтернативно, длина, для которой гелиоцентрическая гравитационная постоянная (произведение G M ☉ ) равна ( 0,017 202 098 95 ) 2 au 3 / d 2 , когда длина используется для описания положения объектов в Солнечной системе.
Последующие исследования Солнечной системы с помощью космических аппаратов позволили получить точные измерения относительного положения внутренних планет и других объектов с помощью радара и телеметрии . Как и все радиолокационные измерения, они основаны на измерении времени, необходимого для отражения фотонов от объекта. Поскольку все фотоны движутся со скоростью света в вакууме, фундаментальной постоянной Вселенной, расстояние от объекта до зонда рассчитывается как произведение скорости света и измеренного времени. Однако для точности расчетов требуется корректировка таких вещей, как движения зонда и объекта во время прохождения фотонов. Кроме того, само измерение времени должно быть переведено в стандартную шкалу, которая учитывает релятивистское замедление времени. Сравнение положений эфемерид с измерениями времени, выраженными в барицентрическом динамическом времени (TDB), приводит к значению скорости света в астрономических единицах в день (из 86 400 с ). К 2009 году IAU обновил свои стандартные меры, чтобы отразить улучшения, и рассчитал скорость света на уровне 173,144 632 6847 (69) а.е. / сут (TDB).
В 1983 году CIPM модифицировал Международную систему единиц (СИ), чтобы измерить метр как расстояние, пройденное светом в вакууме за 1 / 299 792 458 секунд. Это заменило предыдущее определение, действовавшее между 1960 и 1983 годами, которое заключалось в том, что измеритель равнялся определенному количеству длин волн определенной линии излучения криптона-86. (Причиной изменения был улучшенный метод измерения скорости света.) Тогда скорость света можно было бы точно выразить как c 0 = 299 792 458 м / с , стандарт, также принятый числовыми стандартами IERS . Исходя из этого определения и стандарта IAU 2009 года, время прохождения светом астрономической единицы составляет τ A = 499.004 783 8061 ± 0,000 000 01 с , что немного больше , чем 8 минут 19 секунд. Путем умножения лучшая оценка IAU 2009 года была A = c 0 τ A = 149 597 870 700 ± 3 м , на основе сравнения эфемерид Лаборатории реактивного движения и ИАА – РАН .
В 2006 году BIPM сообщил значение астрономической единицы как 1,495 978 706 91 (6) × 10 11 м . В редакции брошюры SI 2014 года BIPM признал, что в 2012 году МАС переопределил астрономическую единицу как 149 597 870 700 м .
Эта оценка по-прежнему была получена на основе наблюдений и измерений, подверженных ошибкам, и основывалась на методах, которые еще не стандартизировали все релятивистские эффекты и, следовательно, не были постоянными для всех наблюдателей. В 2012 году обнаружив, что одно только уравнение относительности сделает определение чрезмерно сложным, МАС просто использовал оценку 2009 года, чтобы переопределить астрономическую единицу как условную единицу длины, напрямую привязанную к метру (точно 149 597 870 700 м ). Новое определение также признает, как следствие, то, что астрономическая единица теперь должна играть меньшую роль, ограниченную в ее использовании удобством в некоторых приложениях.
| 1 астрономическая единица | знак равно 149 597 870 700 метров (точно) |
| ≈ 92 955 807 миль | |
| ≈ 499.004 783 84 световых секунды | |
| ≈ 4,848 1368 × 10 −6 парсек | |
| ≈ 1,581 2507 × 10 −5 световых лет |
Это определение определяет скорость света как 299 792 458 м / с , что в точности равно 299 792 458 × 86 400 ÷ 149 597 870 700 или около 173,144 632 674 240 австралийских единиц в день, что примерно на 60 частей на триллион меньше оценки 2009 года.
Использование и значение
С определениями , используемых до 2012 года, астрономическая единица зависела от гелиоцентрического гравитационных постоянная , то есть произведение гравитационного постоянная , G , и солнечной массы , M ☉ . Ни G, ни M ☉ не могут быть измерены с высокой точностью по отдельности, но значение их произведения очень точно известно из наблюдений за относительным положением планет ( Третий закон Кеплера, выраженный в терминах ньютоновской гравитации). Для расчета положения планет для эфемерид требуется только произведение, поэтому эфемериды рассчитываются в астрономических единицах, а не в единицах СИ.
Расчет эфемерид также требует учета эффектов общей теории относительности . В частности, временные интервалы, измеряемые на поверхности Земли ( Земное время , TT), непостоянны по сравнению с движениями планет: земная секунда (TT) кажется длиннее около января и короче около июля по сравнению с «планетарной секундой». «(условно измеряется в TDB). Это связано с тем, что расстояние между Землей и Солнцем не фиксировано (оно варьируется от 0,983 289 8912 и 1.016 710 3335 а.е. ), и, когда Земля приближается к Солнцу ( перигелий ), гравитационное поле Солнца становится сильнее, и Земля быстрее движется по своей орбитальной траектории. Поскольку метр определяется в единицах секунды, а скорость света постоянна для всех наблюдателей, земной измеритель, кажется, периодически изменяется по длине по сравнению с «планетарным измерителем».
Метр определен как единица надлежащей длины , но определение СИ не указывает метрический тензор, который будет использоваться при его определении. Действительно, Международный комитет мер и весов (CIPM) отмечает, что «его определение применяется только в пределах достаточно малого пространства, чтобы можно было игнорировать эффекты неоднородности гравитационного поля». Таким образом, измеритель не предназначен для измерения расстояний в Солнечной системе. Определение астрономической единицы в 1976 г. было неполным, потому что в нем не указывалась система отсчета, в которой должно измеряться время, но оказалось практичным для вычисления эфемерид: было предложено более полное определение, согласующееся с общей теорией относительности, и дебаты «продолжались до августа 2012 года, когда МАС принял текущее определение 1 астрономическая единица = 149 597 870 700 метров .
Астрономическая единица обычно используется для расстояний в масштабе звездной системы , таких как размер протозвездного диска или гелиоцентрическое расстояние астероида, тогда как другие единицы используются для других расстояний в астрономии . Астрономическая единица слишком мала, чтобы быть удобной для межзвездных расстояний, где широко используются парсек и световой год . Парсек (параллакс угловая секунда ) определяется в астрономических единицах, представляющих собой расстояние до объекта с параллаксом 1 ″ . Световой год часто используется в популярных работах, но он не является утвержденной единицей, не относящейся к системе СИ, и редко используется профессиональными астрономами.
При моделировании числовой модели Солнечной системы астрономическая единица обеспечивает соответствующий масштаб, который минимизирует ( переполнение , потеря значимости и усечение ) ошибки в вычислениях с плавающей запятой .
История
В книге « О размерах и расстояниях Солнца и Луны» , которую приписывают Аристарху , говорится, что расстояние до Солнца в 18-20 раз больше расстояния до Луны , тогда как истинное соотношение составляет примерно 389,174 . Последняя оценка была основана на угле между полумесяцем и Солнцем, который он оценил как 87 ° (истинное значение близко к 89,853 ° ). В зависимости от расстояния, которое, как предполагает ван Хелден, Аристарх использовал для определения расстояния до Луны, его расчетное расстояние до Солнца будет между 380 и 1520 земных радиусов.
Согласно Евсевию Кесарийскому в Praeparatio Evangelica (книга XV, глава 53), Эратосфен обнаружил, что расстояние до Солнца составляет «σταδιων μυριαδας τετρακοσιας και οκτωκισμυριας» (буквально мириады »из 400 стадий 80 000 ″ ), но с дополнительным примечанием, что в греческом тексте грамматическое согласие находится между мириадами (не стадиями ), с одной стороны, и 400 и С другой стороны, 80 000 , как и в греческом, в отличие от английского, все три (или все четыре, если включать стадию ) слова изменяются . Это было переведено как 4 080 000 стадий (1903 перевод по Edwin Hamilton Gifford ), или как 804 000 000 стадионов (издание Édourad des Places , 1974–1991). Используя греческий стадион от 185 до 190 метров, прежний перевод сводится к 754 800 км к 775 200 км , что очень мало, тогда как второй перевод составляет от 148,7 до 152,8 миллиона километров (точность в пределах 2%). Гиппарх также дал оценку расстояния от Земли до Солнца, которое, по словам Паппа, составляет 490 земных радиусов. Согласно гипотетическим реконструкциям Ноэля Свердлоу и Дж. Дж. Тумера , это было получено из его предположения о «наименее заметном» солнечном параллаксе 7 ′ .
Китайский математический трактат Zhoubi Suanjing (ок. I в. До н. Э.) Показывает, как расстояние до Солнца можно вычислить геометрически, используя различную длину полуденных теней, наблюдаемых в трех местах. На расстоянии 1000 ли и предположение, что Земля плоская.
| Расстояние до Солнца оценивается | Оценивать | В Австралии | |
|---|---|---|---|
| Солнечный параллакс | Радиусы Земли | ||
| Аристарх (3 век до н.э.) (в размерах ) | 13 ′ 24 ″ — 7 ′ 12 ″ | 256,5 — 477,8 | 0,011 — 0,020 |
| Архимед (3 век до н.э.) (в песне Reckoner ) | 21 ″ | 10 000 | 0,426 |
| Гиппарх (2 век до н.э.) | 7 ′ | 490 | 0,021 |
| Посидоний (1 век до н.э.) (цитируется ровесником Клеомедом ) | 21 ″ | 10 000 | 0,426 |
| Птолемей (2 век) | 2 ′ 50 ″ | 1,210 | 0,052 |
| Годфрой Венделин (1635) | 15 ″ | 14 000 | 0,597 |
| Иеремия Хоррокс (1639) | 15 ″ | 14 000 | 0,597 |
| Христиан Гюйгенс (1659) | 8,2 дюйма | 25 086 | 1.068 |
| Кассини и Ричер (1672) | 9,5 дюйма | 21 700 | 0,925 |
| Флемстид (1672) | 9,5 дюйма | 21 700 | 0,925 |
| Жером Лаланд (1771) | 8,6 дюйма | 24 000 | 1.023 |
| Саймон Ньюкомб (1895) | 8,80 ″ | 23 440 | 0,9994 |
| Артур Хинкс (1909) | 8,807 ″ | 23 420 | 0,9985 |
| Х. Спенсер Джонс (1941) | 8,790 ″ | 23 466 | 1.0005 |
| современная астрономия | 8,794 143 ″ | 23 455 | 1,0000 |
Во 2 веке нашей эры Птолемей оценил среднее расстояние до Солнца как 1,210 раз Земли радиус . Чтобы определить это значение, Птолемей начал с измерения параллакса Луны, обнаружив, что горизонтальный параллакс Луны составляет 1 ° 26 ′, что было слишком большим. Затем он вывел максимальное расстояние до Луны 64 + 1 / 6 Радиусы Земли. Из-за исключения ошибок в его фигуре параллакса, его теории орбиты Луны и других факторов эта цифра была приблизительно правильной. Затем он измерил видимые размеры Солнца и Луны и пришел к выводу, что видимый диаметр Солнца равен видимому диаметру Луны на наибольшем расстоянии от Луны, и на основании записей лунных затмений он оценил этот видимый диаметр как а также видимый диаметр теневого конуса Земли, пройденный Луной во время лунного затмения. Учитывая эти данные, можно тригонометрически вычислить расстояние от Солнца до Земли. 1,210 земных радиусов. Это дает отношение солнечного расстояния к лунному примерно 19, что соответствует фигуре Аристарха. Хотя процедура Птолемея теоретически работоспособна, она очень чувствительна к небольшим изменениям данных, настолько, что изменение измерения на несколько процентов может сделать расстояние до Солнца бесконечным.
После того, как греческая астрономия была передана средневековому исламскому миру, астрономы внесли некоторые изменения в космологическую модель Птолемея, но не сильно изменили его оценку расстояния Земля-Солнце. Например, во введении к астрономии Птолемея аль-Фергани дал среднее расстояние до Солнца 1170 радиусов Земли, в то время как в его Zij , аль-Баттани использовали среднее солнечное расстояние 1108 радиусов Земли. Последующие астрономы, такие как аль-Бируни , использовали аналогичные значения. Позже в Европе Коперник и Тихо Браге также использовали сопоставимые цифры ( 1,142 и 1150 радиусов Земли), и поэтому приблизительное расстояние Птолемея от Земли до Солнца сохранилось до 16 века.
Иоганн Кеплер был первым, кто понял, что оценка Птолемея должна быть значительно заниженной (по мнению Кеплера, по крайней мере, в три раза) в его таблицах Рудольфина (1627). Законы движения планет Кеплера позволили астрономам вычислить относительные расстояния планет от Солнца и возродили интерес к измерению абсолютного значения для Земли (которое затем могло быть применено к другим планетам). Изобретение телескопа позволило измерять углы гораздо точнее, чем это возможно невооруженным глазом. Фламандский астроном Годфрой Венделин повторил измерения Аристарха в 1635 году и обнаружил, что значение Птолемея было слишком низким, по крайней мере, в одиннадцать раз.
Несколько более точную оценку можно получить, наблюдая прохождение Венеры . Измеряя прохождение в двух разных местах, можно точно рассчитать параллакс Венеры и, исходя из относительного расстояния Земли и Венеры от Солнца, солнечный параллакс α (который нельзя измерить напрямую из-за яркости Солнца). Иеремия Хоррокс попытался произвести оценку на основе своих наблюдений транзита 1639 г. (опубликовано в 1662 г.), давая солнечный параллакс 15 » , похожий на фигуру Венделина. Параллакс Солнца связан с расстоянием Земля – Солнце, измеряемым в радиусах Земли соотношением
А знак равно детская кроватка α ≈ 1 радиан / α . <\ displaystyle A = \ cot \ alpha \ приблизительно 1 \, <\ textrm
Чем меньше солнечный параллакс, тем больше расстояние между Солнцем и Землей: солнечный параллакс 15 ″ эквивалентно расстоянию от Земли до Солнца 13 750 радиусов Земли.
Христиан Гюйгенс считал, что расстояние было еще больше: сравнивая видимые размеры Венеры и Марса , он оценил значение около 24 000 радиусов Земли, что эквивалентно солнечного параллакса 8,6 дюйма . Хотя оценка Гюйгенса удивительно близка к современным оценкам, историки астрономии часто не принимают ее во внимание из-за множества недоказанных (и неверных) предположений, которые он должен был сделать, чтобы его метод работал; Кажется, что точность его оценки основана больше на удаче, чем на удачном измерении, поскольку его различные ошибки взаимно нейтрализуют друг друга.
Жан Ришер и Джованни Доменико Кассини измерили параллакс Марса между Парижем и Кайенной во Французской Гвиане, когда Марс находился ближе всего к Земле в 1672 году. 9,5 ″ , что эквивалентно расстоянию от Земли до Солнца примерно 22 000 радиусов Земли. Они также были первыми астрономами, получившими доступ к точному и надежному значению радиуса Земли, который был измерен их коллегой Жаном Пикаром в 1669 году как 3 269 000 туазов . В этом же году Джон Флэмстид сделал еще одну оценку астрономической единицы , выполнив ее самостоятельно, измерив марсианский суточный параллакс . Другой коллега, Оле Рёмер , открыл конечную скорость света в 1676 году: скорость была настолько велика, что ее обычно называли временем, необходимым свету, чтобы пройти от Солнца до Земли, или «световым временем на единицу расстояния». условность, которой все еще следуют астрономы сегодня.
Лучший метод наблюдения прохождения Венеры был изобретен Джеймсом Грегори и опубликован в его « Оптике Промата» (1663). Эдмонд Галлей решительно отстаивал ее и применял к транзитам Венеры, наблюдаемым в 1761 и 1769 годах, а затем снова в 1874 и 1882 годах. Проходы Венеры происходят парами, но менее одной пары в столетие, и наблюдение транзитов в 1761 и 1769 год стал беспрецедентной международной научной операцией, включая наблюдения Джеймса Кука и Чарльза Грина с Таити. Несмотря на Семилетнюю войну , десятки астрономов были отправлены к наблюдательным точкам по всему миру с большими затратами и личной опасностью: некоторые из них погибли во время попытки. Различные результаты были сопоставлены Жеромом Лаландом, чтобы дать оценку солнечного параллакса 8,6 дюйма . Карл Рудольф Повалки оценил 8,83 дюйма в 1864 году.
| Дата | Метод | A / Gm | Неопределенность |
|---|---|---|---|
| 1895 г. | аберрация | 149,25 | 0,12 |
| 1941 г. | параллакс | 149 674 | 0,016 |
| 1964 г. | радар | 149,5981 | 0,001 |
| 1976 г. | телеметрия | 149 597 870 | 0,000 001 |
| 2009 г. | телеметрия | 149 597 870 700 | 0,000 000 003 |
Другой метод заключался в определении постоянной аберрации . Саймон Ньюкомб придавал большое значение этому методу при выводе широко признанного значения 8,80 ″ для солнечного параллакса (близко к современному значению 8,794 143 ″ ), хотя Ньюкомб также использовал данные транзитов Венеры. Ньюкомб также сотрудничал с А. А. Майкельсоном для измерения скорости света с помощью наземного оборудования; в сочетании с постоянной аберрации (которая связана со световым временем на единицу расстояния), это дало первое прямое измерение расстояния Земля – Солнце в километрах. Значение Ньюкомба для солнечного параллакса (а также для постоянной аберрации и гравитационной постоянной Гаусса) было включено в первую международную систему астрономических констант в 1896 году, которая использовалась для расчета эфемерид до 1964 года. Название «астрономическая единица» кажется, впервые был использован в 1903 году.
Открытие сближающегося с Землей астероида 433 Эрос и его прохождение около Земли в 1900–1901 годах позволило значительно улучшить измерения параллакса. Другой международный проект по измерению параллакса 433 Эроса был предпринят в 1930–1931 годах.
Прямые радиолокационные измерения расстояний до Венеры и Марса стали доступны в начале 1960-х годов. Наряду с улучшенными измерениями скорости света они показали, что значения Ньюкомба для солнечного параллакса и постоянной аберрации несовместимы друг с другом.
Разработки
Единица расстояния A (значение астрономической единицы в метрах) может быть выражена через другие астрономические константы:
А 3 знак равно грамм M ⊙ D 2 k 2 <\ displaystyle A ^ <3>= <\ frac
где G — ньютоновская гравитационная постоянная , M ☉ — масса Солнца, k — численное значение гауссовой гравитационной постоянной, а D — период времени в один день. Солнце постоянно теряет массу, излучая энергию, поэтому орбиты планет неуклонно расширяются в сторону от Солнца. Это привело к призывам отказаться от астрономической единицы как единицы измерения.
Поскольку скорость света имеет точно определенное значение в единицах СИ, а гауссова гравитационная постоянная k фиксирована в астрономической системе единиц , измерение светового времени на единицу расстояния в точности эквивалентно измерению произведения G × M ☉ в единицах СИ. Следовательно, можно построить эфемериды полностью в единицах СИ, что все больше становится нормой.
Анализ радиометрических измерений во внутренней Солнечной системе в 2004 году показал, что вековое увеличение единичного расстояния было намного больше, чем может быть объяснено солнечным излучением. 15 ± 4 метра в столетие.
Измерения вековых вариаций астрономической единицы не подтверждаются другими авторами и весьма противоречивы. Более того, с 2010 года астрономическая единица не оценивалась планетными эфемеридами.
Примеры
В следующей таблице приведены некоторые расстояния в астрономических единицах. Он включает несколько примеров с расстояниями, которые обычно не указываются в астрономических единицах, потому что они либо слишком короткие, либо слишком длинные. Расстояния обычно меняются со временем. Примеры перечислены в порядке увеличения расстояния.
Источник






