§ 12. Законы движения планет Солнечной системы
Важную роль в формировании представлений о строении Солнечной системы сыграли также законы движения планет, которые были открыты Иоганном Кеплером и стали первыми естественно-научными законами в их современном понимании. Работы Кеплера создали возможность для обобщения знаний по механике той эпохи в виде законов динамики и закона всемирного тяготения, сформулированных позднее Исааком Ньютоном. Многие учёные вплоть до начала XVII в. считали, что движение небесных тел должно быть равномерным и происходить по «самой совершенной» кривой — окружности. Лишь Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.
В своих поисках Кеплер исходил из убеждения, что «в мире правит число», высказанного ещё Пифагором. Он искал соотношения между различными величинами, характеризующими движение планет, — размеры орбит, период обращения, скорость. Кеплер действовал фактически вслепую, чисто эмпирически. Он пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон описанных и вписанных в орбиты планет многоугольников и т. д.
Кеплеру необходимо было построить орбиты планет, перейти от экваториальной системы координат, указывающих положение планеты на небесной сфере, к системе координат, указывающих её положение в плоскости орбиты. Он воспользовался при этом собственными наблюдениями планеты Марс, а также многолетними определениями координат и конфигураций этой планеты, проведёнными его учителем Тихо Браге.
Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям. Чтобы построить орбиту Марса, он применил способ, который показан на рисунке 3.5.
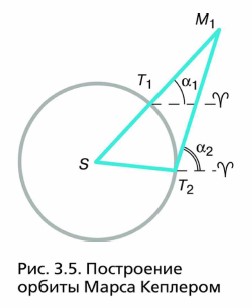
Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты — его прямое восхождение α1, которое выражается углом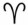 
Т1M1, где Т1 — положение Земли на орбите в этот момент, а M1 — положение Марса. Очевидно, что спустя 687 суток (таков звёздный период обращения Марса) планета придёт в ту же точку своей орбиты. Если определить прямое восхождение Марса на эту дату, то, как видно из рисунка 3.5, можно указать положение планеты в пространстве, точнее, в плоскости её орбиты. Земля в этот момент находится в точке Т2, и, следовательно, угол Т2М1 есть не что иное, как прямое восхождение Марса — α2. Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил ещё целый ряд точек и, проведя по ним плавную кривую, построил орбиту этой планеты.
Изучив расположение полученных точек, он обнаружил, что скорость движения планеты по орбите меняется, но при этом
радиус-вектор планеты за равные промежутки времени описывает равные площади.
Впоследствии эта закономерность получила название второго закона Кеплера.
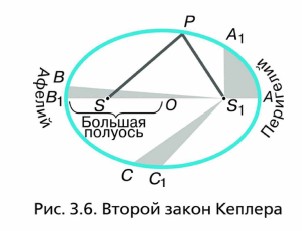
Этот закон, который часто называют законом площадей, иллюстрируется рисунком 3.6. Радиусом-вектором называют в данном случае переменный по своей величине отрезок, соединяющий Солнце и ту точку орбиты, в которой находится планета. АA1, ВВ1, и СС1 — дуги, которые проходит планета за равные промежутки времени. Площади заштрихованных фигур равны между собой.
Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной энергии. По мере приближения планеты к Солнцу возрастает её скорость — увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.
Установив закономерность изменения скорости движения планет, Кеплер задался целью определить, по какой кривой происходит их обращение вокруг Солнца. Он был поставлен перед необходимостью сделать выбор одного из двух возможных решений: 1) считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями (из-за ошибок наблюдений) на 8′; 2) считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью. Будучи уверенным в точности наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом, при этом Солнце не располагается в центре эллипса. В результате был сформулирован закон, который называется первым законом Кеплера.
Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.
Источник
§ 12. Законы движения планет Солнечной системы
Важную роль в формировании представлений о строении Солнечной системы сыграли также законы движения планет, которые были открыты Иоганном Кеплером и стали первыми естественно-научными законами в их современном понимании. Работы Кеплера создали возможность для обобщения знаний по механике той эпохи в виде законов динамики и закона всемирного тяготения, сформулированных позднее Исааком Ньютоном. Многие учёные вплоть до начала XVII в. считали, что движение небесных тел должно быть равномерным и происходить по «самой совершенной» кривой — окружности. Лишь Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.
В своих поисках Кеплер исходил из убеждения, что «в мире правит число», высказанного ещё Пифагором. Он искал соотношения между различными величинами, характеризующими движение планет, — размеры орбит, период обращения, скорость. Кеплер действовал фактически вслепую, чисто эмпирически. Он пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон описанных и вписанных в орбиты планет многоугольников и т. д.
Кеплеру необходимо было построить орбиты планет, перейти от экваториальной системы координат, указывающих положение планеты на небесной сфере, к системе координат, указывающих её положение в плоскости орбиты. Он воспользовался при этом собственными наблюдениями планеты Марс, а также многолетними определениями координат и конфигураций этой планеты, проведёнными его учителем Тихо Браге.
Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям. Чтобы построить орбиту Марса, он применил способ, который показан на рисунке 3.5.
Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты — его прямое восхождение α1, которое выражается углом 
Т1M1, где Т1 — положение Земли на орбите в этот момент, а M1 — положение Марса. Очевидно, что спустя 687 суток (таков звёздный период обращения Марса) планета придёт в ту же точку своей орбиты. Если определить прямое восхождение Марса на эту дату, то, как видно из рисунка 3.5, можно указать положение планеты в пространстве, точнее, в плоскости её орбиты. Земля в этот момент находится в точке Т2, и, следовательно, угол Т2М1 есть не что иное, как прямое восхождение Марса — α2. Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил ещё целый ряд точек и, проведя по ним плавную кривую, построил орбиту этой планеты.
Изучив расположение полученных точек, он обнаружил, что скорость движения планеты по орбите меняется, но при этом
радиус-вектор планеты за равные промежутки времени описывает равные площади.
Впоследствии эта закономерность получила название второго закона Кеплера.
Этот закон, который часто называют законом площадей, иллюстрируется рисунком 3.6. Радиусом-вектором называют в данном случае переменный по своей величине отрезок, соединяющий Солнце и ту точку орбиты, в которой находится планета. АA1, ВВ1, и СС1 — дуги, которые проходит планета за равные промежутки времени. Площади заштрихованных фигур равны между собой.
Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной энергии. По мере приближения планеты к Солнцу возрастает её скорость — увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.
Установив закономерность изменения скорости движения планет, Кеплер задался целью определить, по какой кривой происходит их обращение вокруг Солнца. Он был поставлен перед необходимостью сделать выбор одного из двух возможных решений: 1) считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями (из-за ошибок наблюдений) на 8′; 2) считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью. Будучи уверенным в точности наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом, при этом Солнце не располагается в центре эллипса. В результате был сформулирован закон, который называется первым законом Кеплера.
Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.
Источник
Законы движения планет
В начале 17 века немецкий математик и астроном Иоганн Кеплер вывел три закона движения планет в Солнечной системе. Они были выведены на основании наблюдений за небесными телами, сделанных Браге и другими исследователями космического пространства того времени.
Первый закон Кеплера
Кеплер обратил внимание, что результаты наблюдений Браге расходятся с представлениями о круговой траектории обращения планет вокруг Солнца. Особенно это касалось Марса, чья траектория движения по наблюдения датчанина никак не могла описывать идеальный круг. Браге был очень точен в своих расчетах и сомнений в их правдивости у его последователя не возникло.
Тогда немецкий математик принял орбиты за эллипсы, у каждого из которых есть два фокуса. Это условные точки, выбранные таким образом, что сумма расстояний от них до любой точки эллипса – величина постоянная. При этом для эллиптической орбиты в одном из фокусов находится Солнце.
Форма эллипса вычисляется благодаря отношению фокального расстояния к большой полуоси орбиты. Полученное значение описывает эксцентриситет орбиты. Если он равен нулю – орбита представляет собой идеальную окружность, от нуля до единицы – эллипс различной вытянутости, больше единицы – параболу.
Второй закон Кеплера
Если орбита – это эллипс, то каким образом происходит движение небесного тела по ней? В каких отрезках орбитального пути оно ускоряется и замедляется?
Немецкий ученый обнаружил, что есть взять два любых отрезка орбитального пути, которые планета Солнечной системы проходит за одинаковые промежутки времени, провести от их концов радиус-векторы к центральной звезде, то площади полученных образований будут одинаковы. Это упрощенная формулировка второго закона.
Для того, чтобы постоянство площадей сохранялось, тело должна двигаться в разных точках орбиты с разной скоростью. Так, например, Земля в наибольшем приближении к Солнцу движется быстрее, чем в максимальном удалении от него
Третий закон Кеплера
Третий постулат о движении небесных тел в Солнечной системе как раз касается понятий перигелия и афелия. Если провести между ними условную линию, получится большая ось траектории обращения планеты. Соответственно, половина этого отрезка – большая полуось.
Кеплер на основании наблюдений вывел, что отношение полных оборотов вокруг центральной звезды для двух любых планет системы, возведенных в квадрат, всегда равняется отношению больших полуосей орбитальных путей этих тел, возведенных в куб.
Трудность в доказательстве и принятии трех законов состояла в том, что он вывел их эмпирически. Но в конце 17 века Ньютоном был открыта классическая теория тяготения. Он и помог установить правильность суждений немецкого астронома и описал движение планет по эллипсу вокруг Солнца. Ньютон установил, что кроме массы объекта и его удаления от звезды никакие другие свойства не влияют на гравитационное притяжение.
Также Ньютон внес корректировки и в третий постулат Кеплера. Он открыл, что для соблюдения соотношения необходимо учитывать массу космического объекта. Данная трактовка третьего закона помогает установить массу планеты или спутника, зная величину его орбиты и период обращения.
Законы Иоганна Кеплера помогли установить форму планетарной траектории, вычислить период обращения планет, их скорость и ее изменения по мере приближения и удаления от Солнца. Ученый вывел Землю из ранга особенных астрономических объектов системы и установил, что она подчиняется всем трем законом, как и любая другая планета нашей звездной системы.
Источник