Определение экваториальной координаты солнца

Координаты Солнца

При выполнении инсоляционных расчетов необходимо знать координаты Солнца, определяющие его положение на небосводе в заданный момент времени.

Чтобы представить себе видимое «движение» Солнца по небосводу и определить его координаты, следует обратиться к «солнечному стереону», как это сделал в свое время Витрувий.

Небосвод представляет собой полусферу, опертую на горизонтальный круг, в центре которого находится рассматриваемая точка О. Через эту точку проходят полуденная линия Юг – Север (Ю – С) и линия Восток – Запад (В – З), определяющие ориентацию в данной точке (рис. 32).

Двигаясь по кругу, Солнце занимает на небосводе в данный момент определенное положение, характеризующееся двумя координатами – высотой стояния h и азимутом a (угол между полуденной линией и горизонтальной проекцией солнечного луча, направленного к рассматриваемой точке О от центра солнечного диска). Отсчитывается от Юга к Северу.

Каждый новый день траектория движения Солнца будет выше или ниже предыдущего дня, отличаясь на некоторую угловую величину d, которая называется склонением. В течение года величина склонения изменяется от –23,4 о до +23,4 о , дважды проходя через ноль. Нулевое значение склонения оказывается в те дни, когда Солнце взойдет точно на Востоке и зайдет точно на Западе. При этом день будет равен ночи по продолжительности. 21 марта имеет место день весеннего равноденствия, 23 сентября – день осеннего равноденствия.

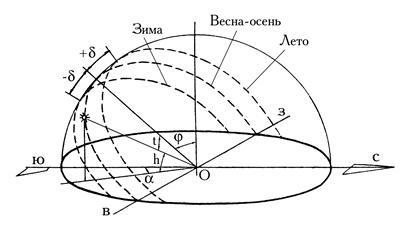
После весеннего равноденствия склонение приобретает положительное значение и достигает своего максимума в день летнего солнцестояния – 21 июня. Далее склонение уменьшается и в день осеннего равноденствия вновь становится равным нулю, после чего приобретает отрицательные значения. Своего минимума склонение достигает 21 декабря в день зимнего солнцестояния. После чего оно снова начинает возрастать и т.д.

За 24 часа Солнце «проходит» по небосводу полный круг» в 360 о . При этом 1 час будет соответствовать 15 о . При расчете координат Солнца время отсчитывают обычно в градусах от линии, образованной пересечением вертикальной плоскости, проходящей через полуденную линию, с плоскостью, в которой лежит видимый путь движения Солнца по небосводу (рис. 32).

Для данного географического пункта плоскость, в которой находится видимый путь движения Солнца по небосводу, имеет наклон относительно вертикальной линии на угол j, который называется географической широтой местности. При этом, на экваторе, где j = 0 о , плоскости видимого движения Солнца вертикальны, а на плюсах, где j = 90 о , — горизонтальны (рис. 33).

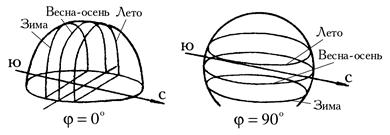
Итак, координаты Солнца на небосводе зависят от склонения, времени суток и географической широты. Взаимосвязь между этими параметрами определяется из следующих выражений:

sina ·cosh = cosd · sint; sinh = sinj ·sind + cosj ·cosd ·cost, (53)

где h – высота стояния Солнца, град;

j — географическая широта, град;

d — склонение Солнца, град;

t — время суток, выраженное в градусах (1час = 15 о );

a — азимут Солнца, град.

Данные формулы позволяют с достаточной степенью точности определить координаты Солнца.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Изменение экваториальных координат Солнца

Эклиптика.

Измерениями зенитного расстояния или высоты Солнца в полдень (т.е. в момент его верхней кульминации) на одной и той же географической широте было установлено, что склонение Солнца в течение года изменяется в пределах от +23° 27′ до —23°27′, два раза в году переходя через нуль. Из наблюдений за изменением вида ночного неба следует, что и прямое восхождение Солнца на протяжении года также постепенно изменяется от 0° до 360°, или от 0h до 24h. Действительно, в полночь в верхней кульминации находятся те звезды, прямые восхождения которых отличаются от прямого восхождения Солнца на 180° или на 12h. Наблюдения же показывают, что с каждым днем в полночь кульминируют звезды все с большим и большим прямым восхождением, следовательно, и прямое восхождение Солнца с каждым днем увеличивается.

Рассматривая непрерывное изменение обеих координат Солнца, нетрудно установить, что оно перемещается среди звезд с запада к востоку по большому кругу небесной сферы, который называется эклиптикой. Плоскость эклиптики E’’ ^ E d
(рис. 11) наклонена к плоскости небесного экватора под углом e = 23° 27′. Диаметр ПП’, перпендикулярный к плоскости эклиптики, называется осью эклиптики и пересекается с поверхностью небесной сферы в северном полюсе эклиптики П (лежащем в северном полушарии) и в южном полюсе эклиптики П’ (в южном полушарии).

Эклиптика пересекается с небесным экватором в двух точках: в точке весеннего равноденствия ^ и в точке осеннего равноденствия d. В точке весеннего равноденствия ^ Солнце пересекает небесный экватор, переходя из южного полушария небесной сферы в северное. В точке осеннего равноденствия d Солнце переходит из северного полушария в южное. Точки эклиптики, отстоящие от равноденственных на 90°, называются точкой летнего солнцестояния (в северном полушарии) и точкой зимнего солнцестояния (в южном полушарии).

Большой полукруг небесной сферы ПМП’, проходящий через полюсы эклиптики и через светило М, называется кругом широты светила.

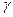
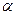
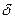
Изменение экваториальных координат Солнца при его движении по эклиптике происходит следующим образом. Когда Солнце находится в точке весеннего равноденствия (см. 2.8), его прямое восхождение и склонение равны нулю. Затем с каждым днем прямое восхождение и склонение Солнца увеличиваются, и когда Солнце придет в точку летнего солнцестояния, его прямое восхождение станет равным 90° или 6h, а склонение достигает максимального значения + 23°27′. После этого склонение Солнца начинает уменьшаться, а прямое восхождение по-прежнему растет. Когда Солнце придет в точку осеннего равноденствия, его прямое восхождение = 180° или 12h, а склонение =0°. Далее, прямое восхождение Солнца, продолжая увеличиваться, в точке зимнего солнцестояния становится равным 270° или 18h, а склонение достигает своего минимального значения — 23° 27′. После этого склонение Солнца начинает расти, и когда Солнце придет в точку весеннего равноденствия, его склонение снова становится равным нулю, а прямое восхождение, достигнув значения 360° или 24h, обращается в нуль.

Эти изменения экваториальных координат Солнца в течение года происходят неравномерно

Движение Земли вокруг Солнца происходит в том же направлении, что и вращение Земли вокруг оси, и неравномерно. При этом ось вращения Земли всегда наклонена к плоскости орбиты Земли под углом 66° 33′. Поэтому нам и кажется, что Солнце так же неравномерно перемещается по небесному своду среди звезд, так же с запада на восток, но по окружности (эклиптике), плоскость которой наклонена к плоскости небесного (и земного) экватора под углом 23°27′ =90°— 66°33′.

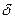
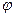
Когда Солнце находится в точке весеннего равноденствия (= 0), то оно на всех географических широтах земной поверхности восходит в точке востока Е и заходит в точке запада W (2.7). Полуденная высота Солнца в день весеннего равноденствия на данной северной широте согласно формуле (2.5)

h¤ = 90° — .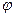

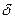
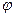
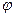
Когда Солнце находится в точке летнего солнцестояния (= +23°27′), то оно восходит на данной северной широте на северо-востоке, а заходит на северо-западе. В день летнего солнцестояния полуденная высота Солнца на данной северной широте достигает максимального значения

h_max = 90° — 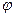+ 23° 27’

Источник

Координаты Солнца

Экваториальные координаты Солнца

Суточное изменение склонения Солнца d в течение месяца до и после дней весеннего и осеннего равноденствия равно 0,4°, в течение месяца до и после дней летнего и зимнего солнцестояний — 0,1°,в течение второго месяца после дней 21.03, 22.06, 23.09, и 22.12—0,3°.

Суточное изменение прямого восхождения Солнца a в течение всего года 1°.

Точные значения координат на любой момент выбирают из Морского астрономического ежегодника (МАЕ).

С помощью приведенных данных можно найти приближенную меридиональную высоту H Солнца на данную дату в широте судна.

Для этого рассчитываем на заданную дату d, затем находим

f — d и H = 90° — Z.

Например, 25 декабря d = 23,2° S. В широте (f = 45,5° N; Z = 45,5° — (— 23,2°) = 68,7°; H = 21,3°.

Легко найти и даты начала и конца полярного дня и ночи. Приближенно условием начала и конца полярного дня принимают d_® = 90° — (f + 1°) при d_® одноименном с f, а условием начала и конца полярной ночи f = 90°— (f—1°), при f разноименном с f.

Изменение f на 1° приближенно учитывает полудиаметр Солнца и астрономическую рефракцию.

Например, в широте 75°N полярный день наступит и закончится при d == 14° N, т. е. соответственно 1 мая и 13 августа, а полярная ночь будет длиться с 7 ноября до 5 февраля.

Источник

Определение экваториальной координаты солнца

В практике широко применяется упрощенный способ определения экваториальных координат Солнца, позволяющий определять их при отсутствии ААЕ. В основу этого способа положены

закономерности годового движения среднего Солнца и истинного, Гринвичский часовой угол истинного Солнца определяется по формуле:

Из приведенной формулы следует, что для определения гринвичского часового угла истинного Солнца необходимо найти часовой угол среднего Солнца и затем учесть поправку к полученному часовому углу на дату полета на величину уравнения времени.

Чтобы упростить указанный расчет, пользуются заранее составленной таблицей (см. приложение 13), в которой для соответствующих часов и минут московского времени указаны гринвичские часовые углы среднего Солнца. Поправки к часовым углам на дату полета определяют по специальному графику (см. рисунок в приложении 13), в котором дано также склонение Солнца. Величина склонения Солнца может быть рассчитана также по формуле

где 23,5° — максимальная величина склонения Солнца; п — количество дней, прошедших после равноденствия или предшествующих равноденствию.

Количество дней, прошедших после равноденствия, берется перед солнцестоянием, а количество дней, предшествующих равноденствию, берется после солнцестояния.

Обычно указанную формулу решают с помощью навигационной линейки. Для этого необходимо треугольный индекс шкалы 4 установить на число 23,5, взятое по шкале 5. Затем против количества дней я, взятого по шкале 3, прочитать по шкале 5 склонение Солнца. Знак склонения определяется в зависимости от положения Солнца на эклиптике.

Рассмотрим на примере порядок определения экваториальных координат Солнца упрощенным способом.

Пример. Дата полета 20 августа. Определить гринвичский часовой угол и склонение Солнца для московского времени .

Решение. 1. Определяем по таблице (см. приложение 13) гринвичский часовой угол среднего Солнца для заданного момента времени:

2. Находим по графику (см. рисунок в приложении 13) поправку к гринвичскому часовому углу на дату полета: .

3. Определяем гринвичский — часовой угол истинного Солнца:

4. Определяем склонение Солнца по графику (см. приложение 13): .

Для расчета склонения Солнца на НЛ находим количество дней, предшествующих равноденствию. От 20 августа до 23 сентября осталось 34 дня. Затем производим действия на НЛ, как это было указано выше, и получаем, что 20 августа склонение Солнца Точность расчета склонения на составляет около 0,5°.

Источник