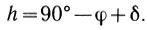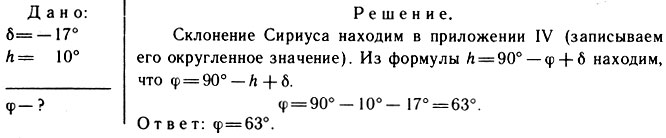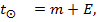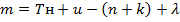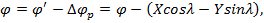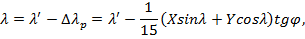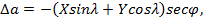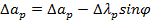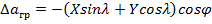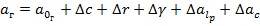Определение географической широты места солнца
Работа N 8. Определение географической широты места
I. По высоте Солнца в полдень
1. За несколько минут до наступления истинного полудня установить теодолит в плоскости меридиана (например, по азимуту земного предмета, как указано в работе N 4). Время наступления полудня вычислить заранее способом, указанным в работе N 3.
 |
| Рис. 56. Положение солнечного диска относительно окулярных нитей теодолита при измерении полуденной высоты Солнца. |
2. С наступлением момента полудня или вблизи него измерить высоту нижнего края диска (фактически верхнего, так как труба дает обратное изображение). Исправить найденную высоту на величину радиуса Солнца (16′). Положение диска относительно перекрестия доказано на рисунке 56.
3. Вычислить широту места, пользуясь зависимостью:
j = 90 – h + d
Дата наблюдения — 11 октября 1961 г.
Высота нижнего края диска по 1 нониусу 27˚58′
Радиус Солнца 16′
Высота центра Солнца 27˚42′
Склонение Солнца — 6˚57
Широта места j = 90 – h + d = 90˚ — 27˚42′ — 6˚57 = 55њ21′
II. По высоте Полярной звезды
1. Пользуясь теодолитом, эклиметром или школьным угломером, измерить высоту Полярной звезды над горизонтом. Это и будет приближенное значение широты с ошибкой около 1˚.
2. Для более точного определения широты с помощью теодолита надо в полученное значение высоты Полярной звезды ввести алгебраическую сумму поправок, учитывающую отклонение ее от полюса мира. Поправки обозначаются цифрами I, II, III и даются в Астрономическом календаре — ежегоднике в разделе «К наблюдениям Полярной».
Широта с учетом поправок вычисляется по формуле: j = h – (I + II + III)
Если учесть, что величина I изменяется в пределах от — 56′ до + 56′ , а сумма величин II + III не превышает 2′, то в измеренную величину высоты можно вводить только поправку I. При этой значение широты получится с ошибкой, не превышающей 2′, что для школьных измерений вполне достаточно (пример введения поправки приводится ниже).
I. При отсутствии теодолита высоту Солнца в полдень можно приближенно определить любым из способов, указанных в работе N 3, или (при недостатке времени) воспользоваться одним из результатов этой работы.
2. Точнее, чем по Солнцу, можно определить широту по высоте звезды в кульминации с учетом рефракции. В этой случае географическая широта определится по формуле:
j = 90 – h + d + R,
где R — астрономическая рефракция 1 .
3. Для нахождения поправок к высоте Полярной звезды необходимо знать местное звездное время в момент наблюдения. Для его определения надо по выверенный по радиосигналам часам отметить сначала декретное время, затем местное среднее время:
Здесь — номер часового пояса, — долгота места, выраженная в часовой мере.
Местное звездное время определяется по формуле 2
где — звездное время в среднюю гринвичскую полночь (оно дается в Астрономическом календаре в разделе «Эфемериды Солнца»).
Пример. Пусть требуется определить широту места в пункте с долготой l = 3ч 55м (IV пояс). Высота Полярной звезды, измеренная в 21ч 15м по декретному времени 12 октября 1964 г, оказалась равной 51˚26′ . Определим местное среднее время в момент наблюдения:
Т= 21 ч 15 м — (4 ч – 3 ч 55 м ) – 1 ч = 20 ч 10 м .
Из эфемерид Солнца находим S0:
S0= 1 ч 22 м 23 с » 1 ч 22 м
Местное звездное время, соответствующее моменту наблюдения Полярной звезды равно:
s = 1 ч 22 м + 20 ч 10 м = 21 ч 32 м .
Из Астрономического календаря величина I равна:
I= + 22′,4
Следовательно, широта
j = 51˚26′ — 22′ = 51˚04′.
1 Среднее значение рефракции вычисляется по формуле:
R= 58,2∙tgZ , если зенитное расстояние Z не превышает 70˚.
2 Здесь не учтена поправка 9˚,86∙(Т- l ), которая никогда не бывает больше 4 мин. К тому же, если не требуется особая точность измерений, то можно в эту формулу вместо Т подставлять Tg . При этом ошибка в определении звездного времени не будет превышать ± 30 мин, а ошибка в определении широты составит не более 5′ — 6′ .
Источник
Определение географической широты места солнца
4. Определение географической широты по астрономическим наблюдениям
1. Высота полюса мира над горизонтом
Обратимся к рисунку 12. Мы видим, что высота полюса мира над горизонтом hp=∠PCN, а географическая широта места φ=∠COR. Эти два угла (∠PCN и ∠COR) равны как углы со взаимно перпендикулярными сторонами: [OC] ⊥[CW], [OR] ⊥[CP]. Равенство этих углов дает простейший способ определения географической широты местности φ: угловое расстояние полюса мира от горизонта равно географической широте местности. Чтобы определить географическую широту местности, достаточно измерить высоту полюса мира над горизонтом, так как:
2. Суточное движение светил на различных широтах
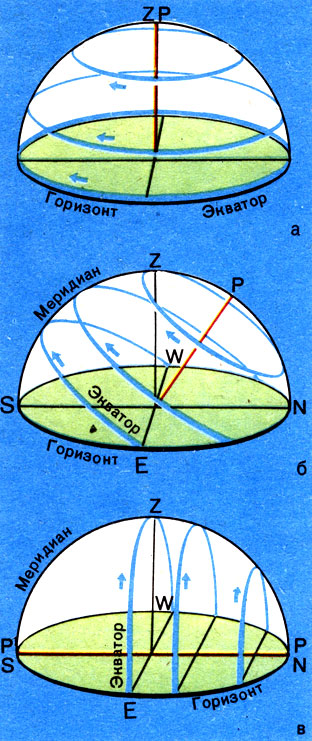
Теперь мы знаем, что с изменением географической широты места наблюдения меняется ориентация оси вращения небесной сферы относительно горизонта. Рассмотрим, какими будут видимые движения-небесных светил в районе Северного полюса, на экваторе и на средних широтах Земли.
На полюсе Земли полюс мира находится в зените, и звезды движутся по кругам, параллельным горизонту (рис. 14, а). Здесь звезды не заходят и не восходят, их высота над горизонтом неизменная.
На средних географических широтах существуют как восходящие и заходящие звезды, так и те, которые никогда не опускаются под горизонт (рис. 14, б). Например, околополярные созвездия (см. рис. 10) на географических широтах СССР никогда не заходят. Созвездия, расположенные дальше от северного полюса мира, показываются ненадолго над горизонтом. А созвездия, лежащие около южного полюса мира, являются невосходящими.
Но чем дальше продвигается наблюдатель к югу, тем больше южных созвездий он может видеть. На земном экваторе, если бы днем не мешало Солнце, за сутки можно было бы увидеть созвездия всего звездного неба (рис. 14, в).
Рис. 14. Суточные пути светил относительно горизонта для наблюдателя, находящегося: а — на полюсе Земли; б — в средних географических широтах; в — на экваторе
Для наблюдателя на экваторе все звезды восходят и заходят перпендикулярно плоскости горизонта. Каждая звезда здесь проходит над горизонтом ровно половину своего пути. Северный полюс мира для него совпадает с точкой севера, а южный полюс мира — с точкой юта. Ось мира расположена в плоскости горизонта (см. рис. 14, в).
Упражнение 2
1. Как по виду звездного неба и его вращению установить, что вы прибыли на Северный полюс Земли?
2. Как суточные пути звезд расположены относительно горизонта для наблюдателя, находящегося на экваторе Земли? Чем они отличаются от суточных путей звезд, видимых в СССР, т. е. в средних географических широтах?
Задание 2
Измерьте при помощи эклиметра географическую широту вашей местности по высоте Полярной звезды и сравните ее с отсчетом широты по географической карте.
3. Высота светил в кульминации
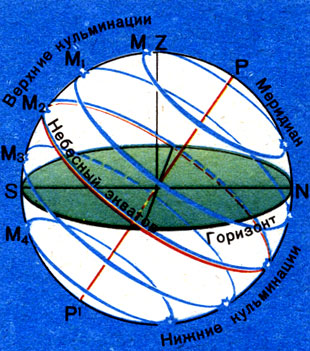
Полюс мира при кажущемся вращении неба, отражающем вращение Земли вокруг оси, занимает неизменное положение над горизонтом на данной широте (см. рис. 12). Звезды за сутки описывают над горизонтом вокруг оси мира круги, параллельные небесному экватору. При этом каждое светило за сутки дважды пересекает небесный меридиан (рис. 15).
Рис. 15. Верхние и нижние кульминации светил
Явления прохождения светил через небесный меридиан относительно горизонта для называются кульминациями. В верхней кульминации высота светила максимальна, а в нижней кульминации — минимальна. Промежуток времени между кульминациями равен половине суток.
У не заходящего на данной широте φ светила М (см. рис. 15) видны (над горизонтом) обе кульминации, у звезд, которые восходят и заходят (M1, М2, М3), нижняя кульминация происходит под горизонтом, ниже точки севера. У светила М4, находящегося далеко к югу от небесного экватора, обе кульминации могут быть невидимы (светило невосходящее).
Момент верхней кульминации центра Солнца называется истинным полднем, а момент нижней кульминации — истинной полночью.
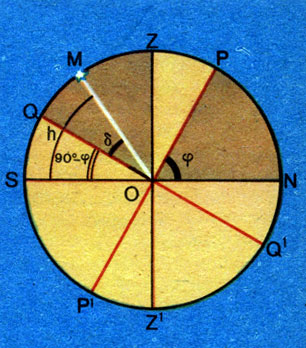
Найдем зависимость между высотой h светила М в верхней кульминации, его склонением δ и широтой местности φ. Для этого воспользуемся рисунком 16, на котором изображены отвесная линия ZZ’, ось мира РР’ и проекции небесного экватора QQ’ и линии горизонта NS на плоскость небесного меридиана (PZSP’N).
Рис. 16. Высота светила в верхней кульминации
Мы знаем, что высота полюса мира над горизонтом равна географической широте места, т. е. hp=φ. Следовательно, угол между полуденной линией NS и осью мира РР’ равен широте местности φ, т.е. ∠PON=hр=φ. Очевидно, что наклон плоскости небесного экватора к горизонту, измеряемый ∠QOS, будет равен 90°-φ, так как ∠QOZ= ∠PON как углы с взаимно перпендикулярными сторонами (см. рис. 16). Тогда звезда М со склонением δ, кульминирующая к югу от зенита, имеет в верхней кульминации высоту
Из этой формулы видно, что географическую широту можно определить, измеряя высоту любого светила с известным склонением δ в верхней кульминации. При этом следует учитывать, что если светило в момент кульминации находится к югу от экватора, то его склонение отрицательно.
Пример решения задачи
Задача. Сириус (α Б. Пса, см. приложение IV) был в верхней кульминации на высоте 10°. Чему равна широта места наблюдения?
Обратите внимание на то, чтобы чертеж точно соответствовал условию задачи.
Упражнение 3
При, решении задач географические координаты городов можно отсчитать по географической карте.
1. На какой высоте в Ленинграде бывает верхняя кульминация Антареса (α Скорпиона, см. приложение IV)?
2. Каково склонение звезд, которые в вашем городе кульминируют в зените? в точке юга?
3. Докажите, что высота светила в нижней кульминации выражается формулой h=φ+δ-90°.
4. Какому условию должно удовлетворять склонение звезды, чтобы она была не заходящей для места с географической широтой φ? невосходящей?
Источник
Вычисление широты места по меридиональной высоте Cолнца
Широту места наблюдателя легко определить, измерив высоту Cолнца в момент верхней кульминации на меридиане наблюдателя. Такая высота Cолнца называется меридиональной. Верхняя кульминация солнца на меридиане (долготе) наблюдателя происходит около полудня. Точное время для каждых суток дано в Астрономическом Ежегоднике (Nautical Almanac).
Пример: 27 ноября 2017 г. Счислимые координаты судна: широта 38° 20, 0′ N; долгота 035°15, 0′ W.
Требуется вычислить время верхней кульминации Cолнца на счислимой долготе и измерить высоту Солнца.
Вычисляем время верхней кульминации Cолнца на счислимой долготе. В Nautical Almanac на дату 27.11.2017 выбираем время верхней кульминации на Гринвиче – 11 h 47 m. Переводим счислимую долготу 035°15, 0′ W в часы и минуты = 02 ч 21 м W. Для этого можно воспользоваться таблицей на стр. 522 в Norie’s Nautical Tables – Conversion of arc to time. Вычисляем гринвичское время верхней кульминации Cолнца на счислимой долготе:
В 14 ч 08 м по Гринвичу измерили секстаном меридиональную высоту нижнего края Cолнца (L.L. – Low Limb) 30° 20, 8′.
Высота глаза наблюдателя 35,5 метров. Атмосферное давление 1018 hPa, температура воздуха + 15°С.
Инструментальная поправка секстана + 0,7′, поправка индекса секстана – 1,5′.
Из Nautical Almanac (N.A.) по дате и гринвичскому времени выбираем склонение Cолнца
Вычисляем широту места наблюдателя по измеренной меридиональной высоте Cолнца:
Источник
Определение Широты по зенитному расстоянию солнца.
Идеальные условия — Солнце необходимо наблюдать вблизи меридиана желательно так, чтобы часть наблюдения была сделана до прохождения Солнцем меридиана, часть – после. Для определения широты достаточно измерить зенитное расстояние Солнца, сопровождая измерения отсчетами по часам. В каждом полуприеме выполняются по два наведения на нижний и верхний край диска Солнца. М и К – впомогательные величины, вычисляемые по следующим формулам:
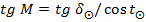
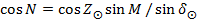
Далее вычисляется широта:
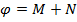
Часовой угол Солнца вычисляется по формуле:
Где
m-среднее солнечное время; u- поправка хронометра; n-номер часового пояса; к-декретный час; λ-долгота.
36.Приведение φ, λи а к среднему полюсу (международному условному началу)
Поправки широты и долготы за приведение к «среднему полюсу» — международному условному началу.
Эти формулы имеют следующий вид:
Где φ и λ – широта и долгота, редуцированные к международному условному началу (МУН), φ’ и λ’ – мгновенные значения широты и долготы, Х и У – координаты мгновенного полюса, выбираемые из бюллетеней «Всемирное время» для эпохи наблюдений. Вторая формула для редукции долготы к «среднему полюсу» получена в предположении, что всемирное время выражено в системе UT1, т.е. отнесено к МУН.
Поправка астрономического азимута за приведение к «среднему полюсу» в системе МУН вычисляется по формуле
Вывод которой дается в сферической астрономии
В этой формуле Х и У – координаты мгновенного полюса эпохи наблюдений, публикуемые в бюллетенях «Всемирное время»; φ и λ – широта и долгота пункта, долгота положительная к востоку от меридиана.
На основании уравнения лапласа поправка геодез азимута, полученного из астрономич наблюдений, за приведение к МУН будет
Подставив в это выражение значение Δа из первой формулы и Δλ получим
Т. О., окончательное значение азимута направления с учетом поправок за приведение к центрам знаков, среднему полюсу и на поверхность эллипсоида будет
Дата добавления: 2018-04-15 ; просмотров: 704 ; Мы поможем в написании вашей работы!
Источник