Пересчет экваториальных координат звезд в эклиптические
При тестировании программы пересчета экваториальных координат небесного объекта в эклиптические установлено, что при заполненной данными расчетной таблице появляется возможность пересчитывать время из представления в часах, минутах и секундах в десятичные доли часа и наоборот, а угловые величины пересчитывать из дробно-десятичного формата в градусах не только в градусы, минуты, секунды, но и в радианы.
В рамках экваториальной системы записи координат эфемериды [2] небесных светил принято представлять в форматах:
угловое расстояние от точки весеннего равноденствия до точки пересечения меридианной линии светила с линией экватора, называемое прямое восхождение α — чч мм сс,сс;
и угловое расстояние вдоль меридиана от точки его пересечения с линией экватора до светила, именуемое как склонение δ — (°) (′) (″,″).
Именно такой формат принят за основной для распознавания в позициях строчного ввода координат небесных объектов (Табл.1). В окна этих позиций вы можете внести скопированные из электронных таблиц координаты небесных объектов.
Во многих случаях будет распознана даже единая строка из двух значений координат, например, такая: 03 ч 24м 19,35c +49° 51′ 40,5″, главное, чтобы присутствовали правильные обозначения водимых угловых координат. Помимо обозначений ч — часы, м — минуты, с — секунды, программа не будет «ругаться» и на представление данных с обозначениями h — hours, m — minutes, s — seconds.
Эклиптическая система небесных координат [3] является древнейшей системой регистрации положения небесных объектов со времен Гиппарха до Байера. Сейчас эта система координат ипользуется для расчетов движения планет, а так же для разбиения небесной сферы на зодиакальные сектора. В наше время принят следующий формат записи эклиптических координат:
долгота λ — (°) (′) (″,″); широта β — (°) (′) (″,″).
Используемая здесь программа позволяет проводить расчет «на лету», реагируя на обновление данных, но пока не введены все необходимые значения .
Для начала расчета нужно ввести или обновить обе пары значений координат звездного объекта. Если необходимое значение координат 0,0000°, то лучше сначала в соответствующую позицию ввести ненулевое значение, а затем, после того как включился зеленый свет для расчетов снова установить 0 (можно просто добавить после нуля точку или запятую, главное, чтобы программа распознала, что все координаты введены осознанно).
Таблица 1: Пересчет координат небесного объекта из экваториальной системы отсчета в эклиптическую
δ — склонение
β — широта
Сближение с Солнцем
Что-то пошло не так. Прямое восхождение не может быть больше 24 часов, минуты и секунды больше 60, а склонение по абсолютной величине не должно быть больше 90°
Design by Sergey Ov for abc2home.ru
Для удобства переноса данных в другие источники предлагаются следующие форматы их вывода:
Объект: Регул
Созвездие: Leo, Лев (Leo)
Экваториальные координаты:
Стандарт — (10ч 08м 22с; 11° 58′ 12″);
Доли часа — (10,13953 ч; 11,97000° );
Градусы — (152,09300°; 11,97000°) или (152.09300, 11.97000)°;
Радианы — (2,65452 рад; 0,20892 рад) или (2.65452, 0.20892) rad
Эклиптические координаты:
Стандарт — (149° 49′ 42″; 0° 28′ 05″);
Градусы — (149,82820°; 0,46810°) или (149.82820, 0.46810)°;
Радианы — (2,61500 рад; 0,00817 рад) или (2.61500, 0.00817) rad
После того как будут введены координаты обоих объектов (планет, звезд) должен погаснуть оранжевый запрос «Данные?» или «?», включится зеленый цвет и автоматически начнется расчет углового расстояния, если это не произошло, то кликните по зеленому полю «Расчет» или «ОК» .
Расчет углового расстояния между двумя астрономическими объектами, положение которых определено во второй экваториальной системе координат
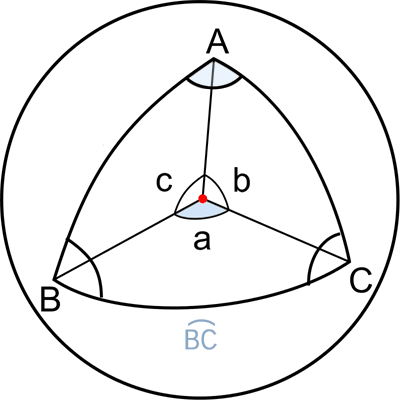
Рис. 1. Сферический треугольник
В основу построения всех уравнений сферической тригонометрии заложено замечательное свойство дуги окружности — радианная мера угла дуги окружности численно равна отношению длины дуги к радиусу этой окружности, например (Рис.1):
Таким образом, все дальнейшие операции проводятся только с угловыми величинами.
В основу выражений зависимостей угловых величин в сферической тригонометрии, так же как и в обычной заложены теоремы синусов и косинусов.
Сферическая теорема косинусов
cos(a) = cos(b)*cos(c)+ sin(b)*sin(c)*cos(A),
cos(b) = cos(c)*cos(a)+ sin(c)*sin(a)*cos(B),
cos(c) = cos(a)*cos(b)+ sin(a)*sin(b)*cos(C).
Сферическая теорема синусов
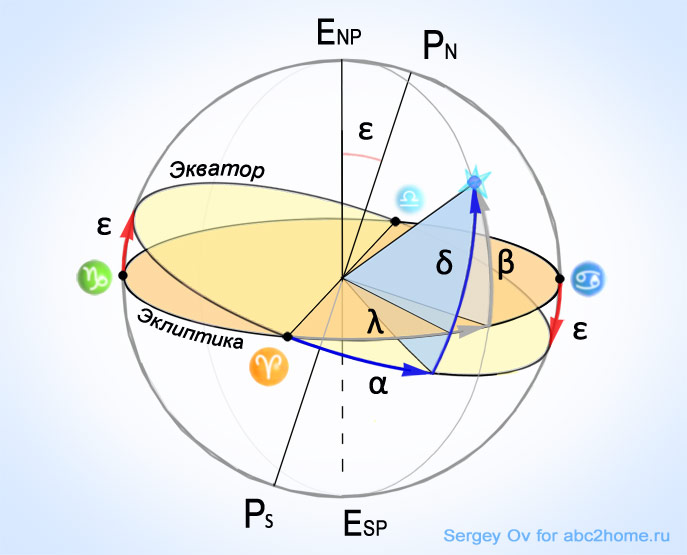
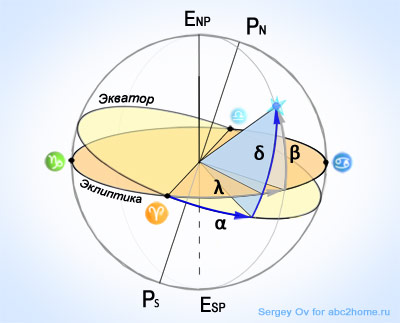
Во второй экваториальной системе координат положение объектов определяется двумя угловыми параметрами, называемыми прямое восхождение α и склонение δ, в эклиптической системе координат аналогичные угловые величины, но привязанные к эклиптике — это долгота λ и широта β (Рис.2).
Рис. 2. Небесная сфера, угловые экваториальные координаты и эклиптические координаты небесного светила (объекта)
Как видно из рисунка, α и δ — прямое восхождение и склонение, характеризующие положение объекта на небесной сфере относительно экватора, соответственно, λ и β долгота и широта, определяющие положение объекта относительно эклиптики.
Склонение определяется величиной угла от линии небесного экватора до объекта в плоскости перпендикулярной экватору.
Прямое восхождение определяется величиной угла между точкой весеннего равноденствия и точкой отсчета склонения.
Важно запомнить, что прямое восхождение отсчитывается от точки весеннего равноденствия в направлении противоположном движению часовой стрелки (в точке весеннего равноденствия Солнце вступает в знак Овна) и его величина выражается не градусах, а в часах. На нашем рисунке величина α составляет примерно 2 часа, а δ чуть-чуть превышает 45°.
Формула расчета углового расстояния выводится с помощью тригонометрических преобразований угловых параметров треугольников соединяющих точки, соответствующие положению объектов на небесной сфере, центр этой сферы и точки отсчета склонений объектов:
sin(β) = cos(ε)*sin(δ) + sin(ε)*sin(α)*cos(δ),
sin(λ)*cos(β) = sin(ε)*sin(δ) + cos(ε)*sin(α)*cos(δ),
cos(λ)*cos(β) = cos(α)*cos(δ),
где ε = 23,439281° представляет собой угол наклона земной оси к эклиптике, то есть угол, который образует плоскость земного экватора с плоскостью земной орбиты при обращении Земли вокруг Солнца.
P.S. На этой странице используется Бета версия программы расчета эклиптических координат точки небесной сферы по заданным экваториальным, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).
1. Эфемеридами называются рассчитанные наперед угловые координаты небесных тел. если подходить к современному понятию строго, то ЭФЕМЕР́ИДЫ (астрономический термин), координаты небесных светил и др. переменные астрономические величины, вычисленные для ряда последовательных моментов времени и сведенные в таблицы.
2. Прямое восхождение и склонение — названия координат во второй экваториальной системе отсчета.
Для определения положения светила s проводят через небесный экватор и Р (полюс мира) большой круг, называемый часовым кругом, или кругом склонений. Дуга этого круга от экватора до светила есть первая координата — склонение светила d (δ). Склонение отсчитывается от экватора в обе стороны от 0° до 90°, причём для светил Южном полушария d (δ) принимается отрицательным.
. Восхождение светила a (α) — дуга α1 небесного экватора (Рис.1), отсчитываемая от точки весеннего равноденствия в направлении, обратном вращению небесной сферы, до круга склонений данного светила. Она измеряет сферический угол между кругами склонений, проходящими через точку равноденствия и данное светило. Обычно ее выражается в часах, минутах и секундах времени и может иметь любое значение от 0ч до 24ч
2. Долгота и широта — названия координат в эклиптической системе отсчета.
В эклиптической системе основным кругом служит эклиптика, полюсом — полюс эклиптики EPN. Для определения положения светила s проводят через него и точку EPN большой круг, называемый кругом широты данного светила. Его дуга от эклиптики до светила называется эклиптической, небесной или астрономической, широтой b (β), является первой координатой. Отсчитывается широта b (β) от эклиптики в направлении к её Северному и Южному полюсам; в последнем случае её считают отрицательной. Вторая координата — эклиптическая, небесная или астрономическая, долгота l (λ) — дуга от /точки весеннего равноденствия/ эклиптики до круга широты данного светила, отсчитываемая в направлении годичного движения Солнца. Она может иметь любое значение от 0 до 360.
4. Астеризм — группа звезд, образующая характерный рисунок и имеющая самостоятельное название. Астеризм может быть как частью созвездия, например, Трон, так и объединять несколько созвездий, например, Зимний Треугольник.
Большой российский энциклопедический словарь. 2012
Источник
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Человек, который никогда не ошибался, никогда не пробовал сделать что-нибудь новое.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля

Урок 02. Звезды и созвездия. Небесные координаты и звездные карты.
2.1.3. Небесные координаты и звездные карты
Чтобы отыскать на небе светило, надо указать, в какой стороне горизонта и как высоко над ним оно находится. С этой целью используется система горизонтальных координат – азимут и высота. Для наблюдателя, находящегося в любой точке Земли, нетрудно определить вертикальное и горизонтальное направления.
Первое из них определяется с помощью отвеса и изображается на чертеже (рис. 1.3) отвесной линией ZZ’, проходящей через центр сферы (точку О).
Точка Z, расположенная прямо над головой наблюдателя, называется зенитом.
Плоскость, которая проходит через центр сферы перпендикулярно отвесной линии, образует при пересечении со сферой окружность – истинный, или математический, горизонт.
Высота светила отсчитывается по окружности, проходящей через зенит и светило, и выражается длиной дуги этой окружности от горизонта до светила. Эту дугу и соответствующий ей угол принято обозначать буквой h.
Высота светила, которое находится в зените, равна 90°, на горизонте – 0°.
Положение светила относительно сторон горизонта указывает его вторая координата – азимут, обозначаемый буквой А. Азимут отсчитывается от точки юга в направлении движения часовой стрелки, так что азимут точки юга равен 0°, точки запада – 90° и т. д.
Горизонтальные координаты светил непрерывно меняются с течением времени и зависят от положения наблюдателя на Земле, потому что по отношению к мировому пространству плоскость горизонта в данном пункте Земли вращается вместе с ней.
Горизонтальные координаты светил измеряют для определения времени или географических координат различных пунктов на Земле. На практике, например в геодезии, высоту и азимут измеряют специальными угломерными оптическими приборами – теодолитами.
Чтобы создать звездную карту, изображающую созвездия на плоскости, надо знать координаты звезд. Для этого нужно выбрать такую систему координат, которая вращалась бы вместе со звездным небом. Для указания положения светил на небе используют систему координат, аналогичную той, которая используется в географии, — систему экваториальных координат.
Система экваториальных координат сходна с системой географических координат на земном шаре. Как известно, положение любого пункта на земном шаре можно указать с помощью географических координат — широты и долготы.
Географическая широта — это угловое расстояние пункта от земного экватора. Географическая широта (φ) отсчитывается по меридианам от экватора к полюсам Земли.
Долгота — угол между плоскостью меридиана данного пункта и плоскостью начального меридиана. Географическая долгота (λ) отсчитывается вдоль экватора от начального (Гринвичского) меридиана.
Так, например, Москва имеет следующие координаты: 37°30′ восточной долготы и 55°45′ северной широты.
Введем систему экваториальных координат, которая указывает положение светил на небесной сфере относительно друг друга.
Проведем через центр небесной сферы (рис. 2.4) линию, параллельную оси вращения Земли, — ось мира. Она пересечет небесную сферу в двух диаметрально противоположных точках, которые называются полюсами мира — Р и Р΄. Северным полюсом мира называют тот, вблизи которого находится Полярная звезда. Плоскость, проходящая через центр сферы параллельно плоскости экватора Земли, в сечении со сферой образует окружность, называемую небесным экватором. Небесный экватор (подобно земному) делит небесную сферу на два полушария: Северное и Южное. Угловое расстояние светила от небесного экватора называется склонением. Склонение отсчитывается по кругу, проведенному через светило и полюса мира, оно аналогично географической широте.
Склонение — угловое расстояние светил от небесного экватора. Склонение обозначают буквой δ. В северном полушарии склонения считают положительными, в южном — отрицательными.
Вторая координата, которая указывает положение светила на небе, аналогична географической долготе. Эта координата называется прямым восхождением. Прямое восхождение отсчитывается по небесному экватору от точки весеннего равноденствия γ, в которой Солнце ежегодно бывает 21 марта (в день весеннего равноденствия). Оно отсчитывается от точки весеннего равноденствия γ против часовой стрелки, т. е. навстречу суточному вращению неба. Поэтому светила восходят (и заходят) в порядке возрастания их прямого восхождения.
Прямое восхождение — угол между плоскостью полукруга, проведенного из полюса мира через светило (круга склонения), и плоскостью полукруга, проведенного из полюса мира через лежащую на экваторе точку весеннего равноденствия (начального круга склонений). Прямое восхождение обозначается буквой α
Склонение и прямое восхождение (δ, α) называют экваториальными координатами.
Склонение и прямое восхождение удобно выражать не в градусах, а в единицах времени. Учитывая, что Земля делает один оборот за 24 ч, получаем:
360° — 24 ч, 1 ° — 4 мин;
15° — 1 ч, 15′ —1 мин, 15″ — 1 с.
Следовательно, прямое восхождение, равное, например, 12 ч, составляет 180°, а 7 ч 40 мин соответствует 115°.
Если не нужна особая точность, то небесные координаты для звезд можно считать неизменными. При суточном вращении звездного неба вращается и точка весеннего равноденствия. Поэтому положения звезд относительно экватора и точки весеннего равноденствия не зависят ни от времени суток, ни от положения наблюдателя на Земле.
Экваториальная система координат изображена на подвижной карте звездного неба.
Принцип создания карты звездного неба весьма прост. Спроектируем сначала все звезды на глобус: там, где луч, направленный на звезду, пересечет поверхность глобуса, будет находиться изображение этой звезды. Обычно на звездном глобусе изображаются не только звезды, но и сетка экваториальных координат. По сути дела, звездным глобусом является модель небесной сферы, которая используется на уроках астрономии в школе. На этой модели нет изображений звезд, но зато представлены ось мира, небесный экватор и другие круги небесной сферы.
Пользоваться звездным глобусом не всегда удобно, поэтому в астрономии (как и в географии) широкое распространение получили карты и атласы.
Атлас звездного неба начинающего наблюдателя
Карту земной поверхности можно получить, если все точки глобуса Земли спроектировать на плоскость (поверхность цилиндра или конуса). Проведя ту же операцию со звездным глобусом, можно получить карту звездного неба.
Познакомимся с простейшей звездной картой, помещенной в Школьном астрономическом календаре.
Расположим плоскость, на которой мы хотим получить карту, так, чтобы она касалась поверхности глобуса в точке, где находится северный полюс мира. Теперь надо спроектировать все звезды и сетку координат с глобуса на эту плоскость. Получим карту, подобную географическим картам Арктики или Антарктики, на которых в центре располагается один из полюсов Земли. В центре нашей звездной карты будет располагаться северный полюс мира, рядом с ним Полярная звезда, чуть дальше остальные звезды Малой Медведицы, а также звезды Большой Медведицы и других созвездий, которые находятся неподалеку от полюса мира. Сетка экваториальных координат представлена на карте радиально расходящимися от центра лучами и концентрическими окружностями. На краю карты против каждого луча написаны числа, обозначающие прямое восхождение (от 0 до 23 ч). Луч, от которого начинается отсчет прямого восхождения, проходит через точку весеннего равноденствия, обозначенную γ. Склонение отсчитывается по этим лучам от окружности, которая изображает небесный экватор и имеет обозначение 0°. Остальные окружности также имеют оцифровку, которая показывает, какое склонение имеет объект, расположенный на этой окружности.
В зависимости от звездной величины звезды изображают на карте кружками различного диаметра. Те из них, которые образуют характерные фигуры созвездий, соединены сплошными линиями. Границы созвездий обозначены пунктиром.
Источник