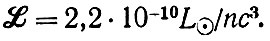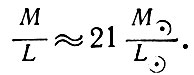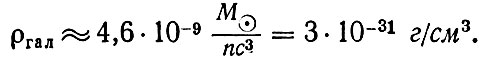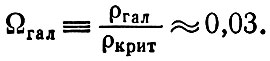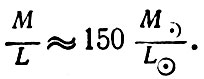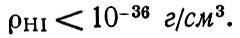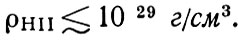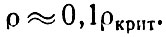Определение средней плотности вещества во вселенной

Определение средней плотности вещества во вселенной

§ 9. Средняя плотность вещества во Вселенной и проблема «скрытой» массы

Вернемся теперь к проблеме средней плотности вещества во Вселенной. Как уже отмечалось, сравнительно несложно учесть «легко наблюдаемое вещество», т. е. вещество, входящее в видимые галактики. Достаточно надежное определение этой величины было сделано в 1958 г. голландским астрономом Оортом. Практическое определение усредненной плотности вещества, входящего в галактики, производится в два приема.

Прежде всего подсчитывается число галактик разных светимостей, приходящихся на единицу объема, и вычисляется средняя светимость единицы объема Вселенной. Согласно Оорту она оказывается равной

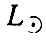
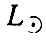
Здесь , обозначает светимость Солнца, равную = 4*10 33 эрг /_сек.

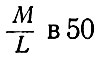
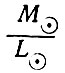
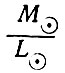
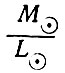
После этого для всех типов галактик вычисляется отношение их массы М к светимости L. Так, для эллиптических галактик отношение раз превышает отношение массы Солнца к его светимости .Для спиральных галактик это отношение M /_L меняется от нескольких единиц до примерно 20 . С учетом процентного содержания разных типов галактик среднее значение M /_L оказывается равным

Произведение (16) и (17) дают усредненную плотность вещества, входящего в галактики,

Эта величина заметно меньше критической плотности (16). Их отношение, обозначаемое обычно буквой Ω, равно

Если во Вселенной нет заметных количеств другой материи, усредненная плотность которой много больше ρ_гал, то Вселенная всегда будет расширяться.

Однако есть серьезные основания подозревать, что в пространстве между галактиками может быть много трудно наблюдаемых форм материи, получивших название «скрытой массы».

Одним из поводов для такого подозрения являются результаты измерений масс скоплений галактик. Измерения проводятся следующим образом.

Правильные скопления имеют симметричную форму, плотность галактик в них плавно спадает от центра к краю и поэтому есть все основания считать, что скопления находятся в равновесном состоянии, когда кинетическая энергия движений галактик уравновешена силой взаимного тяготения всех масс, входящих в скопление.

В этом случае справедлива теорема вириала, утверждающая, что кинетическая энергия всех членов скопления равна по абсолютной величине половине потенциальной энергии тяготения масс скопления (включая, конечно, и невидимые массы). Эта теорема позволяет вычислить полную массу скопления, если известны относительные скорости галактик в скоплении и размер скопления. Относительная скорость галактик в скоплении вычисляется по разности их красных смещений, а размер определяется по угловому размеру скопления на небе и расстоянию от нас. Такое определение, выполненное для уже упоминавшегося нами скопления Coma, приводит к массе порядка 2*10 15 M, что соответствует отношению масса — светимость M /_L для всего скопления (по данным Эйбла)

Полученное отношение во много раз больше, чем M /_L, даже для эллиптических галактик, у которых M /_L наибольшее (сейчас данные пересматриваются). Если эти выводы правильны, то масса скопления много больше суммы масс галактик, в нее входящих. Такие же результаты получаются при рассмотрении других скоплений и групп галактик. Так возникла проблема «скрытой массы». Сразу же оговоримся, что проблема определения массы скоплений с помощью теоремы вириала — сложная задача и здесь возможны ошибки. Основной источник ошибок связан с тем, что скорости галактик измеряются с погрешностями, а это ведет к завышению дисперсии скоростей и, следовательно, к завышению массы скопления. Кроме того, возможна случайная проекция «чужих» галактик на скопление. Учет их также ведет к завышению массы. Однако тщательный анализ показывает, что «свалить» всю вину за получение парадоксально большой массы в скоплениях на подобные ошибки крайне трудно. Полученные выводы заставляют со всей серьезностью отнестись к поискам «скрытой массы», причем не только в скоплениях галактик, но и между скоплениями. В какой форме может существовать скрытая масса? Может быть, это межгалактический газ? * . Ведь объем пространства между галактиками гораздо больше объема пространства, приходящегося на галактики. Поэтому межгалактический газ, концентрация которого хотя и много меньше, чем у газа внутри галактик, может в результате все же давать гигантские массы.

* ( Анализом наблюдений, связанным с поисками межгалактического газа, занимались многие астрофизики. Мы отметим здесь работы советских ученых В. Л. Гинзбурга, Я. Б. Зельдовича, И. С. Шкловского, А. Г. Дорошкевича, В. Г. Курта, Л. М. Озерного, Р. А. Сюняева и др.)

Прежде всего напомним, что газ во Вселенной в основном состоит из водорода. Следовательно, чтобы установить наличие газа в межгалактическом пространстве, в первую очередь надо искать водород. В зависимости от физических условий газ может быть в нейтральном и ионизованном состояниях.

Начнем с оценки возможного количества нейтрального водорода.

Если свет от далекого источника идет через газ с нейтральными атомами водорода, то происходит поглощение (говоря точнее, резонансное рассеяние) излучения атомами в спектральной линии L_α с длиной волны λ = 1215 Å. Это ведет к ослаблению света от источника на данной длине волны. В качестве источников используются далекие квазары. Атомы водорода расположены на всем огромном пути от квазара и имеют поэтому разную скорость удаления от нас вследствие расширения Вселенной по закону Хаббла (v = HR). Разные скорости поглощающих атомов ведут к тому, что из-за эффекта Доплера линия поглощения в спектре растягивается в полосу. Тщательные поиски этого эффекта в спектрах квазаров с z > 2 не привели к успеху, полосы поглощения не обнаружено. Отсюда делается вывод, что средняя плотность числа нейтральных атомов в межгалактическом газе ничтожна: n_HI -11 см 3 , а соответствующая плотность вещества

Аналогичные соображений применимы и для молекулярного водорода (поглощение в лаймановской полосе молекулярного водорода). Наблюдения приводят к выводу, что и плотность молекулярного водорода в межгалактическом газе пренебрежимо мала.

Таким образом, межгалактический газ, если он и есть, должен быть ионизованным, а значит, и сильно нагретым. Как показывает анализ, для этого необходимы температуры больше миллиона градусов. Не следует удивляться, что несмотря на такую температуру этот газ практически невидим. Дело в том, что плотность его очень мала, газ прозрачен, излучает мало видимого света. Но все же эта ионизованная высокотемпературная плазма испускает достаточно много ультрафиолетового излучения и мягких рентгеновских лучей.

Горячий газ можно искать по ультрафиолетовому излучению. Однако этот метод оказался не очень чувствительным.

Интересный метод был предложен советским астрофизиком Р. А. Сюняевым. Он основан на следующих соображениях. Ультрафиолетовый поток излучения от горячего межгалактического газа должен ионизовать водород на периферии галактик. Но радиоастрономические способы наблюдений позволили обнаружить нейтральный водород на окраинах нашей и других галактик. Расчет показывает, что если бы плотность горячего межгалактического газа равнялась критической ρ_{H И} = 10 -29 г /_{см 3} , то поток ультрафиолетового излучения от него полностью бы ионизовал водород на периферии галактик, в противоречии с наблюдениями. Следовательно,

Эта величина много больше ргал. Таким образом, к сожалению, рассматриваемый метод все же недостаточно чувствителен, чтобы исключить возможность существования большого количества горячего межгалактического газа. Вопрос о количестве такого газа, о том, больше ли его усредненная плотность, чем усредненная плотность вещества, входящего в галактики, остается открытым.

Обратимся теперь к газу в скоплениях галактик. Радионаблюдения показывают, что нейтрального водорода в скоплениях ничтожно мало. Однако с помощью рентгеновских телескопов, установленных на спутниках, был обнаружен горячий ионизованный газ в богатых скоплениях галактик. Оказалось, что этот газ нагрет до Т ≈ 10 8 К. Его полная масса может доходить до 10 13 М. Цифра внушительная, но мы видели выше, что полная масса скопления Coma, определенная по теореме вириала, гораздо больше — превышает 10 15 M д. Таким образом, наличие горячего газа в скоплениях никак не исчерпывает проблемы скрытой массы.

Несколько лет назад у этой пресловутой проблемы выявился еще один аспект.

В последнее время появляется все больше сторонников идеи о том, что галактики могут быть окружены огромными массивными коронами слабо светящихся объектов, которые по их свечению обнаружить крайне трудно. Это могут быть, например, звезды низкой светимости. Масса этих звезд в коронах не влияет заметно на динамику внутренних частей галактик * , которые хорошо наблюдаются, и поэтому наблюдения этих внутренних частей дают только их массу и ничего не говорят о массах корон. Но масса короны должна влиять на движение карликовых галактик — спутников основной галактики. Именно по этому влиянию и пытаются обнаружить в настоящее время короны галактик. Возможно, что учет этих корон существенно изменит оценку масс галактик в скоплениях и решит проблему «скрытой массы». Однако в настоящее время вопрос о коронах галактик еще не решен.

* ( Вспомним, что сферическая оболочка не создает гравитационного поля во внутренней полости (см. § 2 гл. 1).)

Нам остается еще разобрать вопрос об экзотических кандидатах на роль скрытой массы, таких как космические лучи, нейтрино, гравитационные волны, а также и другие виды физической материи.

Наблюдения показывают, что плотность массы, соответствующая космическим лучам, не более 10 -35 г /_{см 3} , т. е. очень мала.

Что касается нейтрино и гравитационных волн, то тут дело обстоит сложнее. Взаимодействие этих видов физической материи с обычным веществом крайне слабое и поэтому, если бы Вселенная была заполнена нейтрино или гравитационными волнами с плотностью массы (соответствующей плотности энергии по формуле Эйнштейна е = ρс 2 ) даже больше ρ_крит, то все равно прямые физические методы не позволили бы их обнаружить. Есть косвенные соображения о малой вероятности большого количества этих экзотических форм материи. С некоторыми соображениями мы познакомимся в дальнейшем.

Итак, подытоживая сказанное, мы видим, что вопрос о среднем значении плотности вещества р во Вселенной пока не решен. В § 4 гл. 2 мы еще раз вернемся к этому вопросу и рассмотрим способ определения ρ, не зависящий от конкретной природы физической материи, а использующий тот факт, что любая масса создает поле тяготения. Правда, и этот универсальный метод не привел пока к успеху.

Здесь же в заключение приведем мнение большинства специалистов о наиболее вероятном значении средней плотности всех видов материи во Вселенной, полученном на основе всех способов наблюдений.

Это наиболее вероятное значение есть

Истина в науке не устанавливается подсчетом большинства голосов специалистов, но читателю полезно знать, что по мнению этих самых специалистов плотность материи во Вселенной не превышает критического значения и Вселенной предстоит неограниченное расширение.

Источник

Определение средней плотности вещества во вселенной

§ 4. Средняя плотность вещества во Вселенной и наблюдательное исследование кривизны пространства

Кривизну трехмерного пространства можно определить вычислением, зная постоянную Хаббла и плотность вещества. Но, к сожалению, плотность вещества; как мы видели выше, известна столь плохо, что не определен даже знак кривизны пространства — положительна она или отрицательна.

А нельзя ли обратить задачу? Нельзя ли измерить кривизну пространства и уже по кривизне вычислить плотность ρ? При этом автоматически будет определено р с учетом видов вещества — и трудно наблюдаемого и легко наблюдаемого. Один путь исследования кривизны — это наблюдение зависимости m ÷ z для очень далеких галактик (или квазаров). Вычисления по формулам релятивистской космологии показывают, что для далеких объектов зависимость m ÷ z должна отклоняться от прямолинейной зависимости, которая была нами описана в гл. 1 в рамках классической механики и электродинамики. Отклонение от прямой линии зависит от кривизны пространства. На рис. 20 а нанесены разные кривые, соответствующие разной кривизне и, следовательно, разной плотности ρ. Из рисунка видно, что данные наблюдений не позволяют пока определить, больше ли ρ, чем ρ_крит или нет? Другой способ определения кривизны пространства состоит в подсчетах галактик (или радиоисточников) до данной видимой звездной величины. Эта зависимость должна быть разная для пространств с разной кривизной. При этом истинная яркость галактик считается известной, или хотя бы постоянной для разных объектов. На пути таких исследований имеется много технических трудностей. Но помимо трудностей технических, существует принципиальная трудность. От далеких источников мы наблюдаем свет, испущенный давно, т. е. это свет, испущенный объектами, находящимися на более ранней стадии развития по сравнению с близкими объектами. Поэтому прежде чем определять ρ из графиков типа риc. 20а, надо учесть эволюцию галактик — изменение их светимости, спектра и т. п. Как эволюционируют галактики, практически совсем не известно, и выводы о значении ρ остаются очень неопределенными.

_крит; 2) ρ = 5 ρ_крит; 3) ρ = 2 ρ_крит; 4) кривая, соответствующая теории стационарной Вселенной; см. § 5 гл. 5″>
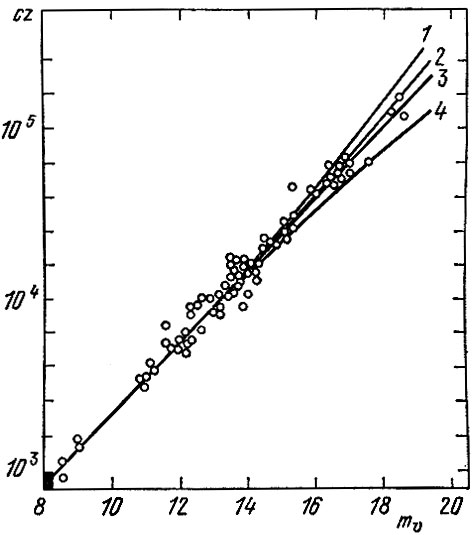
Рис. 20 а. Зависимость m ÷ z с теоретическими кривыми для разной плотности 1) ρ = 10 ρ_крит; 2) ρ = 5 ρ_крит; 3) ρ = 2 ρ_крит; 4) кривая, соответствующая теории стационарной Вселенной; см. § 5 гл. 5

Большие надежды в космологии возлагались на радиоастрономию. Чувствительность радиотелескопов огромна. Однако оказалось, что радиоизлучение галактик меняется со временем еще сильнее, чем оптическое излучение, и радиоастрономия также не дала решения проблемы кривизны пространства. Этот вопрос продолжает стоять на повестке дня науки.

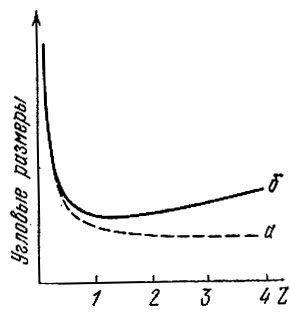
Отметим любопытное явление, которое должно наблюдаться в однородной Вселенной. Пусть мы наблюдаем в обычном пустом плоском пространстве объекты одинакового линейного размера (например, одинаковые галактики), находящиеся на разных расстояниях. Чем дальше объект, тем меньше угол, под которым мы видим объект (рис. 20 б). Угловой размер объекта будет обратно пропорционален расстоянию.

Рис. 20 б. Зависимость углового размера объекта от красного смещения: а) когда в конусе лучей нет вещества; б) когда в конусе лучей есть вещество

Иная картина должна наблюдаться в пространстве в среднем равномерно заполненном прозрачным веществом, например, прозрачным газом или перекрывающимися коронами галактик. Из общей теории относительности известно, что лучи света, проходящие вблизи тяготеющих масс, отклоняются ими, притягиваются. Таково знаменитое отклонение на 1″,75 лучей света звезд, когда лучи проходят вблизи поверхности Солнца. Поэтому газ, находящийся в конусе лучей от далеких галактик, будет изгибать их, как схематически показано на рис. 20 б. Чем дальше объект, тем большая масса содержится в конусе лучей, тем больше отклонение. Это приводит к тому, что, начиная с некоторого расстояния, более далекий объект имеет уже не меньшие угловые размеры, а большие, чем более близкий! Разумеется, этот эффект будет иметь место только тогда, когда в конусе лучей есть газ (или другая материя). Если же вещество сосредоточено только в галактиках, межгалактическое пространство пусто и в конусе лучей совсем нет вещества, то даже несмотря на высокую среднюю плотность галактик, в пространстве для пустого конуса лучей этот эффект отсутствует. На это обстоятельство обратил внимание Я. Б. Зельдович.

Источник