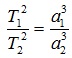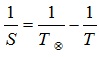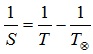Определить массу солнца используя расстояние от солнца до земли

Как измерить массу Земли и массу Солнца?

Простая и надежная методика измерения массы космических тел — как узнать сколько весит Солнце, зная лишь силу притяжения между космическими телами

Как можно измерить вес (точнее, массу) Солнца, если даже реальный размер нашей “домашней звезды” настолько велик, что просто не укладывается в голове? Наверняка тут должен быть какой-то секрет… И подумав так, вы будете правы и не правы одновременно.

На первый взгляд, идея измерить массу Солнца, кажется фантастикой. На самом деле для этого не понадобится ничего, кроме простейших вычислений

С одной стороны, никакого секрета в деле измерения массы любого небесного тела сколько угодно большого размера, конечно же нет. С другой стороны, без определенных хитростей тут, конечно, не обойтись.

Давайте сразу условимся – говоря, что “нам нужно определить массу Солнца”, мы имеем ввиду “определить количество вещества входящего в состав Солнца”.

Для начала измерим массу Земли

Переформулировав задачу таким образом, мы сразу же получим зацепки ведущие к решению. Первым делом нам нужно определить величину силы притяжения возникающей между любыми двумя массами.

Принцип этого определения следующий:

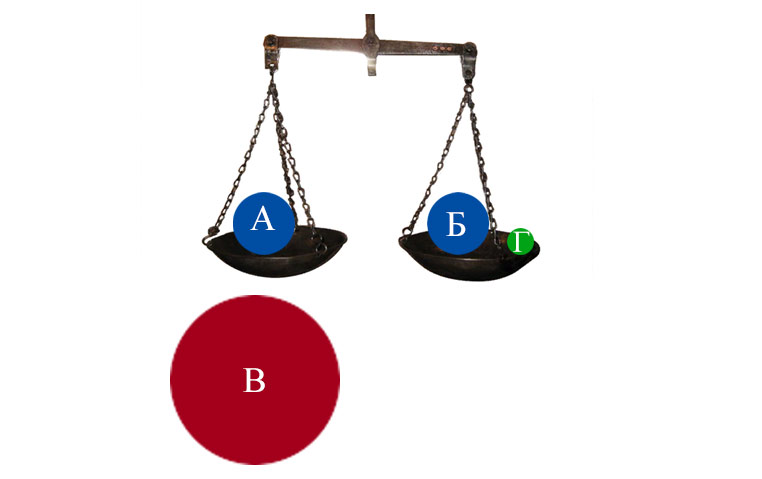
Представьте себе очень при очень чувствительные равноплечие весы с двумя чашками. В каждой чашке (А и Б) пускай лежит некий груз имеющий совершенно одинаковую массу. Весы в таком случае, будут прибывать в полном равновесии.

Теперь мы берем третье тело (В) масса которого нам также известна, и помещаем его под тело А. Взаимное притяжение между А и В, ожидаемо заставляет чашку весов А опуститься вниз. Для сохранения равновесия нам срочно необходимо добавить к массе Б очень небольшую, но опять же вполне измеримую массу Г.

Как вычислить массу планеты Земля, не выходя из дома?

Вас может заинтересовать

А вот теперь самое интересное: поскольку сила, с которой вся Земля притягивает тело Г, равна взаимному притяжению между А и В, можно без труда определить массу Земли, которая оказывается равной 6,59 х 10 21 тонн.

А теперь измерим массу Солнца!

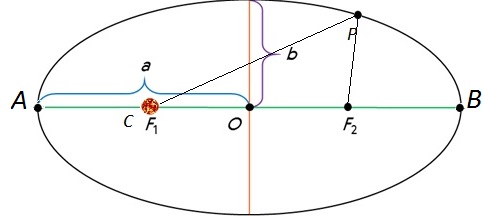
Земля по своей орбите движется примерно так, как если бы невидимая нить соединяла ее с Солнцем. Действительно, гравитационное притяжение подобно натяжению нити, так что Земля все время движется к Солнцу, вместо того чтобы «улететь» по прямой линии, что будет, если эта “нить” вдруг оборвется. Можно сказать, что, двигаясь вокруг Солнца, Земля все время «падает» на него.

Этому “падению” соответствует отклонение ее орбиты от прямой линии, составляющее около 3 мм в секунду. Еще со времен Галилея известно, что на поверхности Земли в первую секунду своего падения всякое тело проходит 4,9 м. Расстояния 3 мм и 4,9 м прямо пропорциональны соответствующим гравитационным ускорениям, т. е. силам, действующим на единичную
массу со стороны Солнца на расстоянии Земли и Земли на ее поверхности.

Отсюда, зная, что гравитационное ускорение прямо пропорционально массе и обратно пропорционально квадрату расстояния от центра тела, можно легко вычислить, что масса Солнца в 329 390 раз больше массы Земли.

Воспользовавшись значением массы Земли, полученным выше, находим, что масса Солнца составляет 2.24 х 10 27 тонн. Полностью это немыслимое число можно записать, как 2 240 000 000 000 000 000 000 000 000 тонн.

Влияние силы тяготения на движение Земли. Путь А-С представляет собой путь пройденный Землей по орбите за 1 секунду (30 км), при этом отклонение от прямой линии B-C составит всего 3 миллиметра

Читайте также: Кроткое солнце это какое

Теперь уже можно вычислить и среднюю плотность Солнца, т. е. его массу, поделенную на массу воды, занимающей тот же объем.

Поскольку один кубический сантиметр воды весит один грамм, мы просто должны разделить массу Солнца (в граммах) на его объем (в кубических сантиметрах). Получим в результате число 1,42.

Иными словами, в среднем некоторый объем солнечного вещества должен весить приблизительно столько же, сколько ком битумного угля, занимающего такой же объем.

Естественно, “среднее значение” на то и среднее, чтоб представлять некую золотую середину между солнечным ядром (где плотность вещества в 10 раз превышает плотность стали) и веществом солнечной короны (где плотность падает почти до величины космического вакуума). Тем не менее, в общем и целом данная методика расчетов абсолютно верна и может с успехом применяться при расчете массы любого небесного тела – хоть астероида, хоть звезды.

Источник

ИНФОФИЗ — мой мир.

Весь мир в твоих руках — все будет так, как ты захочешь

Как сказал.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»

Тема: Законы Кеплера. Определение масс небесных тел

Цель занятия: Освоить методику решения задач, используя законы движения планет.

Теоретические сведения

При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.

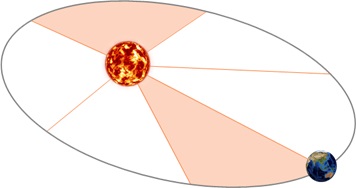
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.

Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:

Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:

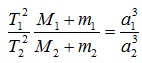
где М₁ и М₂ -массы каких-либо небесных тел, а m₁ и m₂ — соответственно массы их спутников.

Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:

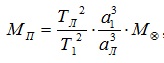
где Т_л и α _л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.

Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,

а) для внешней планеты формула имеет вид:

б) для внутренней планеты:

Выполнение работы

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.

Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.

Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.

Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?

Примеры решения задач 1-4

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Источник

Солнечная масса — Solar mass

Основная информация Система единиц астрономия Единица масса Символ M _☉ В базовых единицах СИ (1,988 47 ± 0,000 07 ) × 10 30 кг

Масса Солнца ( M _☉ ) — стандартная единица массы в астрономии , приблизительно равная 2 × 10 30 кг . Он часто используется для обозначения массы других звезд , а также звездных скоплений , туманностей , галактик и черных дыр . Это примерно равно массе Солнца . Это равно примерно двум нониллионам (короткая шкала) или двум квинтиллионам ( длинная шкала ) килограмм:

M _☉ = (1,988 47 ± 0,000 07 ) × 10 30 кг

Солнечная масса около 333 000 раз больше массы Земли ( M _⊕ ), или 1047 раз больше массы Юпитера ( M _J ).

СОДЕРЖАНИЕ

История измерений

Значение гравитационной постоянной было впервые получено из измерений, которые были выполнены Генри Кавендишем в 1798 году с помощью торсионных весов . Полученное им значение всего на 1% отличается от современного значения, но не так точно. Суточный параллакс Солнца был точно измерен во время транзитов Венеры в 1761 и 1769, что дает значение 9 ″ (9 угловых секунд по сравнению с текущим значением 8,794 148 ″ ). По величине суточного параллакса можно определить расстояние до Солнца, исходя из геометрии Земли.

Первая известная оценка солнечной массы была сделана Исааком Ньютоном . В своей работе « Начала» (1687) он подсчитал, что отношение массы Земли к Солнцу составляет около 1 ⁄ 28700 . Позже он определил, что его значение было основано на неверном значении солнечного параллакса, которое он использовал для оценки расстояния до Солнца. Он исправил свое оценочное отношение к 1 / 169282 в третьем издании Principia . Текущее значение солнечного параллакса меньше , тем не менее, с получением , по оценкам , массовое соотношение 1 / 332946 .

В качестве единицы измерения масса Солнца вошла в употребление до того, как были точно измерены а.е. и гравитационная постоянная. Это связано с тем, что относительная масса другой планеты в Солнечной системе или объединенная масса двух двойных звезд может быть рассчитана в единицах солнечной массы непосредственно из радиуса орбиты и периода обращения планеты или звезд с использованием третьего закона Кеплера.

Расчет

Масса Солнца не может быть измерена напрямую, и вместо этого рассчитывается из других измеримых факторов, используя уравнение для периода обращения небольшого тела, вращающегося вокруг центральной массы. В зависимости от длины года, расстояния от Земли до Солнца ( астрономическая единица или а.е.) и гравитационной постоянной ( G ) масса Солнца определяется путем решения третьего закона Кеплера :

M ⊙ знак равно 4 π 2 × ( 1 А U ) 3 грамм × ( 1 у р ) 2 <\ Displaystyle M _ <\ odot>= <\ frac <4 \ pi ^ <2>\ times (1 \, \ mathrm ) ^ <3>> ) ) ^ <2>>>>

Значение G трудно измерить, и оно известно только с ограниченной точностью ( см. Эксперимент Кавендиша ). Значение G, умноженное на массу объекта, называемое стандартным гравитационным параметром , известно для Солнца и нескольких планет с гораздо большей точностью, чем для одного G. В результате масса Солнца используется как стандартная масса в астрономической системе единиц .

Вариация

Солнце теряет массу из-за реакций синтеза, происходящих в его ядре, ведущих к излучению электромагнитной энергии , а также из-за выброса вещества с солнечным ветром . Это изгнание о (2-3) × 10 -14 M _☉ в год. Скорость потери массы увеличится, когда Солнце войдет в стадию красного гиганта , поднявшись на (7–9) × 10 −14 M _☉ y −1, когда он достигает вершины ветви красных гигантов . Это будет расти до 10 — 6 М _☉ у -1 на асимптотической ветви гигантов до пика со скоростью 10 -5 до 10 -4 М _☉ у -1 , как Солнце генерирует планетарную туманность . К тому времени, когда Солнце станет вырожденным белым карликом , оно потеряет 46% своей начальной массы.

Масса Солнца уменьшалась с момента его образования. Это происходит с помощью двух процессов в почти равных количествах. Во-первых, в ядре Солнца водород превращается в гелий посредством ядерного синтеза , в частности p – p-цепи , и эта реакция преобразует некоторую массу в энергию в виде гамма- квантов. Большая часть этой энергии в конечном итоге излучается от Солнца. Во-вторых, протоны и электроны высоких энергий в атмосфере Солнца выбрасываются непосредственно в космическое пространство в виде выбросов солнечного ветра и корональной массы .

Первоначальная масса Солнца в то время, когда оно достигло главной последовательности, остается неопределенной. Раннее Солнце имело гораздо более высокие темпы потери массы, чем в настоящее время, и оно могло потерять где-то от 1 до 7% своей натальной массы за время своей жизни на главной последовательности. Солнце приобретает очень небольшую массу из-за удара астероидов и комет . Однако, поскольку Солнце уже содержит 99,86% общей массы Солнечной системы, эти удары не могут компенсировать потерю массы из-за излучения и выброса.

Связанные единицы

Одна солнечная масса, M _☉ , может быть преобразована в соответствующие единицы:

В общей теории относительности также часто бывает полезно выражать массу в единицах длины или времени.

Параметр солнечной массы ( G · M _☉ ), указанный Рабочей группой IAU Division I, имеет следующие оценки:

1,327 124 420 99 (10) × 10 20 м 3 с −2 ( совместимость с TCG )
1,327 124 400 41 (10) × 10 20 м 3 с −2 ( TDB- совместимый)

Источник