Решебник по астрономии 11 класс на урок №19 (рабочая тетрадь) — Солнце как звезда
вкл. 28 Ноябрь 2016 .
Решебник по астрономии 11 класс на урок №19 (рабочая тетрадь) — Солнце как звезда
1. Руководствуясь схемой строения Солнца, укажите названия внутренних областей и слоёв атмосферы Солнца.
| 1 | Зона ядерных реакций | 4 | Фотосфера |
| 2 | Зона переноса лучистой энергии | 5 | Хромосфера |
| 3 | Зона конвекции | 6 | Корона |
| (4, 5, 6) | Атмосфера | 7 | Солнечный ветер |
2. Заполните таблицу с основными характеристиками Солнца.
| Параметры | Величины |
| Среднее расстояние от Земли | 1 а. е. |
| Линейный диаметр | 109 D |
| Видимый угловой диаметр | 32′ |
| Масса | 330000 M |
| Солнечная постоянная | 1.37 кВт/м 2 |
| Светимость | 3,85 ⋅ 10 26 Вт |
| Температура видимого внешнего слоя | 5800 К |
| Химический состав внешних слоёв | -73% — H, — 25% — He, -2% — др. |
| Период вращения | 25 сут — у экватора, 30 сут — у полюса |
| Температура в центре Солнца | -15 000 000 К |
| Абсолютная звёздная величина | -48 |
| Возраст | -4,57 млрд лет |
| Средняя плотность | 1,41 ⋅ 10^3 кг/м 3 |
3. Определите линейный радиус Солнца (в радиусах Земли и километрах). Угловой радиус фотосферы и расстояние от Земли до Солнца Считайте известными.
4. Определите массу Солнца, если Земля обращается вокруг Солнца на расстоянии 1 а. е. с периодом один год. Орбиту Земли считайте круговой.
5. Звезда Ригель из созвездия Орион излучает света примерно в 60 тыс. раз больше нашего Солнца. Объясните почему же тогда Солнце выглядит ярче, чем Ригель?
Решение: Солнце — ближайшая к нам звезда, и она в 23 млн раз ближе, чем Ригель.
6. Определите светимость Солнца, если солнечная постоянная равна 1370 Вт/м, а расстояние от Земли до Солнца — 1 а. е.
7. Определите температуру фотосферы, если светимость Солнца равна 3,85 ⋅ 10 26 и радиус Солнца — 696 тыс. км.
Источник
Урок 10
Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а. е.), которая равна среднему расстоянию от Земли до Солнца.
1 а.е. = 149 600 000 км
Расстояние до объекта по времени прохождения радиолокационного сигнала можно определить по формуле , где S = 1/2·ct, где S — расстояние до объекта, c — скорость света, t — время прохождения светила.
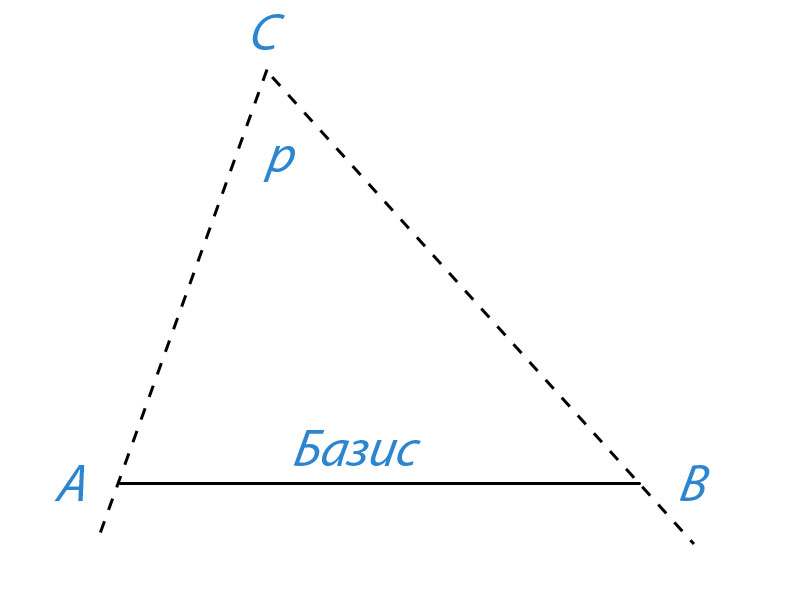
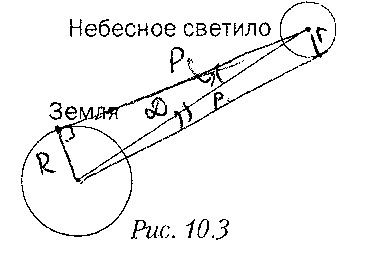
Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом.
Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B.
По величине базиса и прилегающим к нему углам треугольника ABC найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.
r = D · sin(ρ); R = D · sin(ρ)/sin(p) · R; r = ρ/p · R.
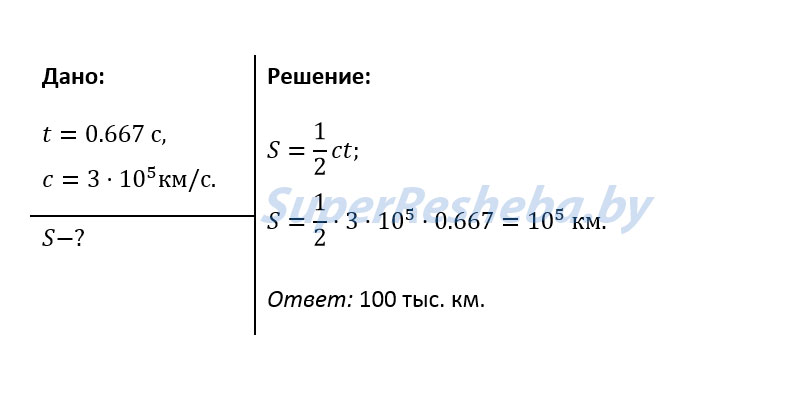
1. Радиолокатор зафиксировал отраженный сигнал от пролетающего вблизи Земли астероида через t — 0,667 с. На каком расстоянии от Земли находился в это время астероид?
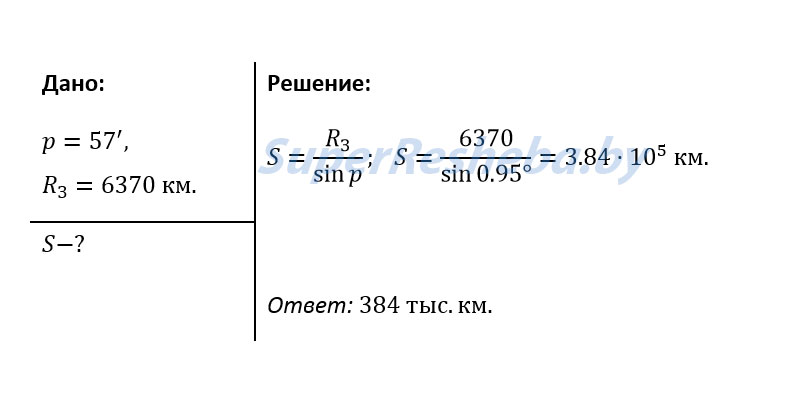
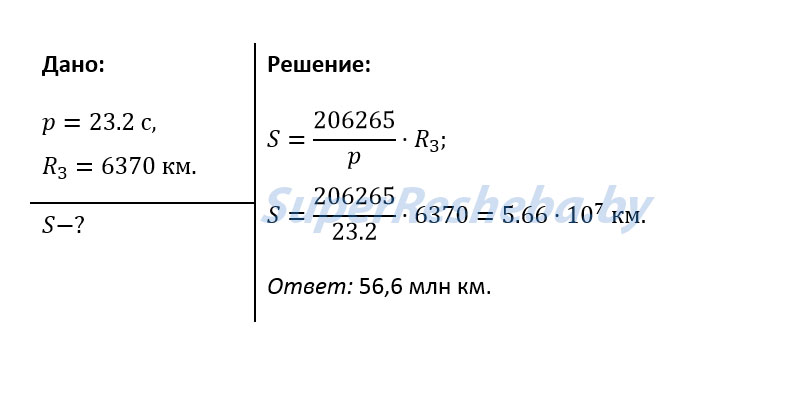
2. Определите расстояние от Земли до Марса во время великого противостояния, когда его горизонтальный параллакс p = 23,2″.
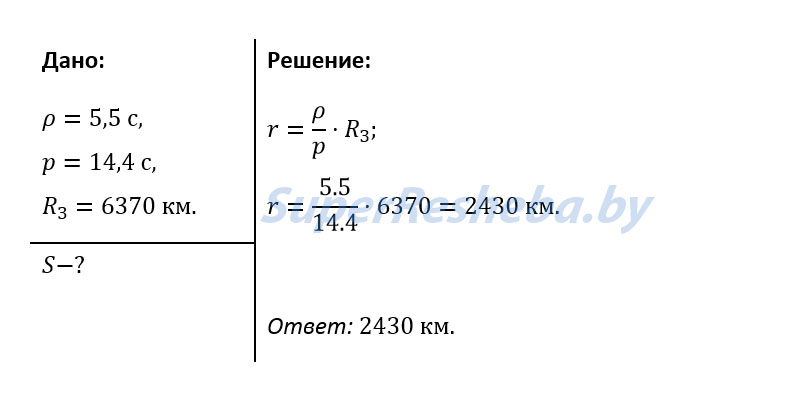
3. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус p = 5,5″, а горизонтальный параллакс p = 14,4″. Определите линейный радиус Меркурия.
1. Сигнал, посланный радиолокатором к Венере, возвратился назад через t — 4 мин 36 с. На каком расстоянии в это время находилась Венера в своем нижнем соединении?
Ответ: 41 млн км.
2. На какое расстояние к Земле подлетал астероид Икар, если его горизонтальный параллакс в это время был p = 18,0″?
Ответ: 1,22 млн км.
3. С помощью наблюдений определили, что угловой радиус Марса p = 9,0″, а горизонтальный параллакс p = 16,9″. Определите линейный радиус Марса.
Источник
Определите линейный радиус солнца если его угловой радиус 16
Работа N 7. Определение угловых и линейных размеров Солнца (или Луны)
I. С помощью теодолита.
1. Установив прибор и вставив светофильтр в окуляр трубы, совместить нуль алидады с нулем горизонтального лимба. Закрепить алидаду и при открепленном лимбе навести трубу на Солнце так, чтобы вертикальная нить касалась правого края диска Солнца (это достигается с помощью микрометрического винта лимба). Затем быстрым вращением микрометрического винта алидады перевести вертикальную нить на левый край изображения Солнца. Сняв показания с горизонтального лимба, и получают угловой диаметр Солнца.
2. Вычислить радиус Солнца по формуле:
R = D ∙ sin r
где r — угловой радиус Солнца, D — расстояние до Солнца.
3. Для вычисления линейных размеров Солнца можно воспользоваться и другой формулой. Известно, что радиусы Солнца и Земли связаны с расстоянием до Солнца соотношением:
R = D ∙ sin r ,
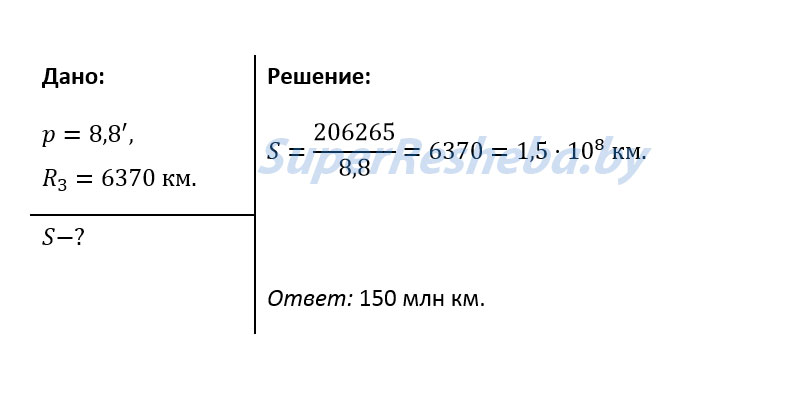
R0 = D ∙ sin p,
где r — угловой радиус Солнца, а p — его параллакс.
Поделив почленно эти равенства, получим:
Ввиду малости углов, отношение синусов можно заменить отношением аргументов.
Тогда 
Значения параллакса р и радиуса Земли берутся из таблиц.
| R0= 6378 км, |  |
| r = 16′ | |
| p = 8″,8 |
Отношение 
Аналогично определяются и размеры Луны.
II. По времени прохождения диска светила через вертикальную нить оптической трубы
Если смотреть на Солнце (или Луну) в неподвижный телескоп, то вследствие суточного вращения Земли светило будет постоянно уходить из поля зрения телескопа. Для определения углового диаметра Солнца, с помощью секундомера измеряют время прохождения его диска через вертикальную нить окуляра и найденное время умножают на cos d , где d — склонение светила 1 . Затем время переводят в угловые единицы, помня, что за 1 мин Земля поворачивается на 15′, а за 1 сек. — на 15″. Линейный диаметр D определяется из соотношения:

где R — расстояние до светила, a — его угловой диаметр, выраженный в градусах.
Если использовать угловой диаметр, выраженный в единицах времени (например, в секундах), то
где t — время прохождения диска через вертикальную нить, выраженное в секундах.
Дата наблюдения — 28 октября 1959 г.
Время прохождения диска через нить окуляра t = 131 сек.
Склонение Солнца на 28 октября d = — 13њ.
Угловой диаметр Солнца a = 131∙ cos 13њ = 131∙0,9744 = 128 сек. или в угловых единицах a = 32 = 0,533њ.
| Линейный диаметр Солнца |  |
1. Из двух способов второй более доступен. Он проще по технике выполнения и не требует какой-либо предварительной тренировки.
2. Проводя такие измерения, интересно отметить разницу в величине видимого диаметра Солнца, когда оно бывает в перигее и апогее. Разница эта составляет около 1′ или по времени — 4 сек.
В значительно больших пределах изменяется видимый диаметр Луны (от 33′,4 до 29′,4). Это хорошо видно из рис. 55. Здесь уже разница во времени — около 16 сек.

Рис. 55. Наибольший и наименьший видимые размеры диска Луны, расположенные концентрически (слева) эксцентрически (справа).
Такие наблюдения будут воочию убеждать учащихся в том, что орбиты Земли и Луны не круговые, а эллиптические (иллюстрация к законам Кеплера).
3. Пользуясь вторым способом, можно определять размеры некоторых лунных образований, длину теней от гор и др.
Источник
Примеры решения расчетных задач
Задача 1. Как часто повторяются противостояния Марса, сидерический период S которого 1,9 года?
Очевидно, нужно найти синодический период этой (верхней) планеты. Для этого воспользуемся формулой:

где TЗ – сидерический период Земли, T – сидерический период Марса.
Тогда 
Ответ: S = 2,1 года.
Задача 2. Вычислите массу Юпитера, зная, что один из его спутников (Ио) обращается вокруг планеты с периодом 1,77 сут. на расстоянии 422 000 км. (Сравните движение Ио вокруг Юпитера с движением Луны вокруг Земли. Период обращения Луны вокруг Земли 27,32 сут., среднее расстояние от Земли составляет 384 000 км).
Решение:
Для решения задачи необходимо воспользоваться третьим уточненным законом Кеплера:

Принимая за первую пару Юпитер с Ио ( M1 – масса Юпитера, m1 – масса Ио, a1 – большая полуось орбиты Ио), а за вторую – Землю с Луной ( M2 – масса Земли, m2 – масса Луны, a2 – большая полуось орбиты Луны), а также пренебрегая массой спутников по сравнению с массой планет, получим:

Задача 3. Во сколько раз линейный радиус Солнца превышает радиус Земли, если угловой радиус Солнца равен 16′?
Решение:
Воспользуемся формулами п. 5.4, гл. 5 пособия.
Обозначим 



Ответ: 
Задача 4. Флаг корабля привязан к мачте на высоте 30 метров над уровнем моря. На каком расстоянии l он будет виден на горизонте?
Решение:
Выполним рисунок (рис. 2).
Здесь h – высота флага над уровнем моря, R – радиус Земли. Ясно, что (R + h) 2 = R 2 + l 2 . Тогда

если принять за R, например, средний экваториальный радиус Земли.
Ответ: l ≈ 19,56 км.
Дата добавления: 2014-11-24 ; просмотров: 7 | Нарушение авторских прав
Источник
Определите линейный радиус солнца если его угловой радиус 16
Экзаменационные билеты по астрономии
1. Солнце как типичная звезда. Основные характеристики.
2. Определение условий видимости планеты Марс по данным «Школьного астрономического календаря». скачать
1. Важнейшие проявления Солнечной активности. Их связь с географическими явлениями.
2. Определение условий видимости планеты Юпитер по данным «Школьного астрономического календаря». скачать
1. Способы определения расстояний до звёзд. Единицы расстояний и связь между ними.
2. Определение условий видимости планеты Луны по данным «Школьного астрономического календаря». скачать
1. Основные физические характеристики звёзд и их взаимосвязь. Условия равновесий звезд.
2. Вычисление линейных размеров светила по известным угловым размерам и расстоянию.
Пример: С Земли с помощью своего телескопа наблюдатель различает на Луне объекты протяженностью 1 км. Определите объекты какого размера можно разглядеть в телескоп на Марсе. Расстояние от Земли до Луны 3,8 × 10 5 км, до Марса 1,0 × 10 8 км. скачать
1. Физический смысл закона Стефана-Больцмана и его применение для определения физических характеристик звёзд.
2. Определение географической широты места наблюдения по заданной высоте светила в кульминации и его склонению.
П ример: Какова географическая широта места наблюдения, если звезда Регул наблюдалась в верхней кульминации на высоте 57°? скачать
1. Переменные и нестационарные звёзды. Их значение для изучения природы звёзд.
2. Вычисление склонения светила по данным о его высоте в кульминации на определенной географической широте.
Пример: Наблюдатель увидел яркую звезду на высоте 49 о над горизонтом. Что за звезду видит человек, если известно, что он проводит свое наблюдение в г. Бобруйске. скачать
1. Двойные звёзды и их роль в определении физических характеристик звёзд.
2. Вычисление высоты светила в кульминации по известному склонению для данной географической широты.
Пример: Какой наибольшей высоты достигает Вега ( h = +38 о 42 / ) в Бобруйске ( j = 53 о )? скачать
1. Эволюция звёзд, её этапы и конечные стадии.
2. Наблюдение и зарисовка положения солнечных пятен с помощью телескопа (на экране). скачать
1. Состав, структура и размер нашей Галактики.
2. Вычисление радиуса звезды по данным о ее светимости и температуре.
Пример: Определите радиус звезды в радиусах солнца, если известно, что ее температура в два раза превышает солнечную, а светимость в 100 раз. скачать
1. Звёздные скопления, физическое состояние межзвёздной среды.
2. Вычисление угловых размеров Солнца для наблюдателя, находящегося на другой планете.
Пример: Во сколько раз линейный радиус Солнца превышает радиус Земли, если угловой радиус Солнца 16 / ? Горизонтальный параллакс Солнца 8,8 // .
Пример: Каков угловой диаметр Солнца, рассматриваемого с Нептуна? скачать
1. Основные типы галактик и их отличительные особенности.
2. Определение условий видимости планеты Сатурн по данным «Школьного астрономического календаря». скачать
1. Основы современных представлений о строении и эволюции Вселенной.
2. Вычисление расстояния до звезд по известному параллаксу.
П ример: Параллакс Альтаира 0,20 // . Чему равно расстояние до этой звезды в парсеках? в световых годах? скачать
Смотрите новый сайт В. Грабцевича по физике, а также шутки про школу.
Источник