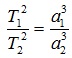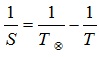Урок 8
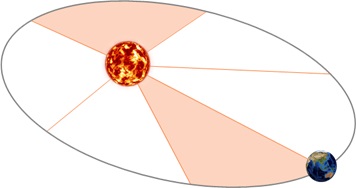
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
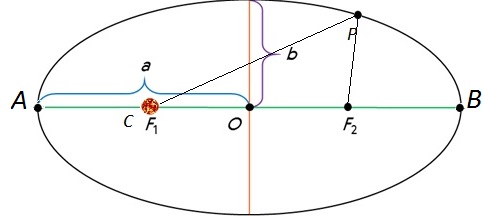
Перигелийное расстояние $ПС = q$; афелийное расстояние $СА = Q$. $АП = 2a$; $ПО = ОА = a$. Тогда: $q = ОП — СО$; $e = \dfrac<СО><ОП>$; $СО = e · a$; $Q = ОА + СО$; $q = a — ea = a(1 — e)$; $Q = a + ea = a(1 + e)$.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
- а) скорость планеты максимальна;
- б) потенциальная энергия максимальна;
- в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
- а) скорость планеты минимальна;
- б) потенциальная энергия минимальна;
- в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
вкл. 27 Ноябрь 2016 .
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
1. Сформулируйте законы Кеплера.
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
2. На рисунке 8.1 укажите точки афелия и перигелия.
3. Выведите формулы для вычисления перигелийного и афелийного расстояний по известным эксцентриситету и значению большой полуоси.
Перигелийное расстояние ПС = q; афелийное расстояние СА = Q. АП = 2a; ПО = ОА = a. Тогда: q = ОП — СО; e = СО/ОП; СО = e · a; Q = ОА + СО; q = a — ea = a(1 — e); Q = a + ea = a(1 + e).
4. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а = 2,88 а. е., а эксцентриситете = 0,24.
5. Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а = 160 млн км, а эксцентриситет е = 0,83.
6. Выполните задание.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
а) скорость планеты максимальна;
б) потенциальная энергия максимальна;
в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
а) скорость планеты минимальна;
б) потенциальная энергия минимальна;
в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
7. Решите задачи.
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник
Урок 8
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
Перигелийное расстояние $ПС = q$; афелийное расстояние $СА = Q$. $АП = 2a$; $ПО = ОА = a$. Тогда: $q = ОП — СО$; $e = \dfrac<СО><ОП>$; $СО = e · a$; $Q = ОА + СО$; $q = a — ea = a(1 — e)$; $Q = a + ea = a(1 + e)$.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
- а) скорость планеты максимальна;
- б) потенциальная энергия максимальна;
- в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
- а) скорость планеты минимальна;
- б) потенциальная энергия минимальна;
- в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник
Законы движения планет Солнечной системы
Описание презентации по отдельным слайдам:
Законы движения планет Солнечной системы Урок астрономии в 11 классе .
Интеллектуальная разминка 1. Измеренное секстантом угловое расстояние планеты от Солнца оказалось равным 60°. Определите, какая это планета — верхняя или нижняя. 2. Можно ли наблюдать Венеру утром на западе, а вечером на востоке? Почему? Возможно ли подобное наблюдение для Меркурия; Марса? 3. Сидерический период обращения Марса вокруг Солнца составляет 686,97 сут. Определите, через какой промежуток времени Земля видна с Марса как утреннее светило Меркурий Венера Земля Марс
Прокомментируйте: «…Коперник впервые создал научную картину мира, заложив тем самым, по словам академика Амбарцумяна, «первый камень в фундамент современного естествознания»… «…Человек, несомненно, достигнет других планет и, может быть, других миров, когда физикой будут открыты новые, еще более эффективные источники энергии. Как бы ни были велики дальнейшие успехи науки, имя гениального сына польского народа Николая Коперника будет вечно сиять, как ярчайшая звезда» Ф. М. Дягилев «Из истории физики и жизни ее творцов» М. В. Келдыш «Николай Коперник»
«…явление, которое отличает научную мысль и результаты от просто утверждений, — общеобязательность и бесспорность» Тема урока: Законы движения планет Солнечной системы В. И. Вернадский
С древнейших времен считалось, что небесные тела движутся по «идеальным кривым» — окружностям. Клавдий Птолемей (ок. 90 – ок. 160) Геоцентрическая система Птолемея
В теории Николая Коперника, создателя гелиоцентрической системы мира, круговое движение также не подвергалось сомнению. Гелиоцентрическая система мира Коперника Николай Коперник (1473–1543)
Иоганн Кеплер (1571–1630 ) Тихо Браге (1546-1601) В XVII веке Иоганн Кеплер, изучая движение Марса по результатам многолетних наблюдений датского астронома Тихо Браге, обнаружил, что орбита Марса не окружность, а имеет вытянутую форму эллипса.
Логика рассуждений И. Кеплера И. Кеплер пришел к формулировке законов эмпирическим путем, базируясь на гелиоцентрическом устройстве Солнечной системы и убежденности в том, что, согласно Пифагору, «миром правят числа»
Важнейшие точки и линии эллипса F, F’-фокусы орбиты а – длина большой полуоси е –эксцентриситет (сжатие) е = ОF/ ОA
Первый закон Кеплера Иллюстрация первого закона Кеплера на примере движения спутников Земли Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.
Большая полуось орбиты планеты – это ее среднее расстояние от Солнца. Среднее расстояние Земли от Солнца принято в астрономии за единицу расстояния и называется астрономической единицей: 1 а.е. = 149 600 000 км. Ближайшую к Солнцу точку орбиты называют перигелием (греч. пери – возле, около; Гелиос – Солнце), а наиболее удаленную – афелием (греч. апо – вдали).
Второй закон Кеплера (закон площадей) Радиус-вектор планеты за равные промежутки времени описывает равные площади. Иллюстрация второго закона Кеплера на примере движения спутника Земли
Перигелий Афелий М1 М2 М3 М4 Планеты движутся вокруг Солнца неравномерно: линейная скорость планет вблизи перигелия больше, чем вблизи афелия. У Марса вблизи перигелия скорость равна 26,5 км/с, а около афелия — 22 км/с. У некоторых комет орбиты настолько вытянуты, что вблизи Солнца их скорость доходит до 500 км/с, а в афелии снижается до 1 см/с. Перигелий Афелий
Третий закон Кеплера Квадраты сидерических периодов обращений двух планет относятся как кубы больших полуосей их орбит:
Пример решения задачи
Задачи 1. Вычислите период обращения Нептуна вокруг Солнца, если среднее расстояние от Солнца составляет 30 а. е. 2. Определите величину большой полуоси орбиты Сатурна, если его синодический период обращения равен 378 сут. 3. Период обращения вокруг Солнца одного из крупнейших тел главного пояса астероидов — Весты — составляет 3,6 года. Во сколько раз среднее расстояние от Весты до Солнца больше, чем среднее расстояние от Солнца до Земли?
Ответьте на вопросы Какое расстояние называется астрономической единицей? Чему равна 1 а. е.? Что такое эллипс? Назовите важнейшие точки и линии эллипса Сформулируйте законы Кеплера Сформулируйте значение данных законов
Рефлексия сегодня я узнал… было интересно… было трудно… я выполнял задания… я понял, что… теперь я могу… я почувствовал, что… я приобрел… я научился… у меня получилось … я смог… я попробую… меня удивило… урок дал мне для жизни… мне захотелось…
Источник
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Все знают, что это невозможно. Но вот приходит невежда, которому это неизвестно — он-то и делает открытие.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
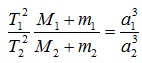
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
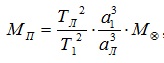
где Тл и α л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Источник