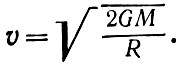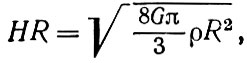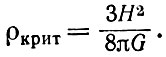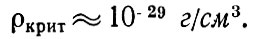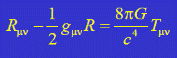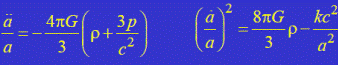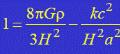Определите значение критической плотности для модели расширяющейся вселенной

§ 30. Расширяющаяся Вселенная

1. Опишите пространственное распределение галактик во Вселенной.

Галактики образуют группы, скопления и большие системы галактик. Из 40 ближайших галактик наиболее массивная — Местная группа галактик. В эту группу входят наша Галактика и туманность Андромеды. Они образуют систему галактик, размер которых достигает нескольких сотен килопарсек.

Системы галактик могут объединять до тысячи галактик, а их размеры достигают нескольких мегапарсек. Ближайшее такое крупное объединение находится в направлении созвездия Девы на расстоянии около 20 Мпк., имеет размер примерно в 5 Мпк.

Комплексы скоплений галактик содержат десятки скоплений и имеют размеры 30-60 Мпк. Такие комплексы называют сверхскоплениями галактик. Наша Местная группа галактик входит в скопление в созвездии Девы разером 60 Мпк, которое объединяет около 2000 галактик. Всего известно около 50 сверхскоплений.

2. Как объясняется красное смещение и о чём оно свидетельствует?

Красное смещение в спектрах галактик свидетельствует о постоянном расширении Вселенной, «разлёту» скоплений галактик.

3. В чём состоит сущность теории расширяющейся Вселенной?

Сущность теории состоит в том, что Вселенная не может быть стационарна — она должна либо расширяться, либо сжиматься. Расширение Вселенной обнаружил Э. Хаббл, когда зафиксировал разбегание галактик.

4. К каким выводам о стационарности Вселенной пришёл А. А. Фридман?

Из расчётов Фридмана вытекали три возможных следствия: Вселенная и её пространство расширяются с течением времени; Вселенная через определённое время начнёт сжиматься; во Вселенной чередуются через большие промежутки времени циклы сжатия и расширения.

5. Что такое критическая плотность Вселенной? В какой взаимосвязи критическая плотность находится с расширением или сжатием Вселенной?

Существует значение критической плотности $ρ_<кр>$ Вселенной, определяемое по формуле:

где $G$ — гравитационная постоянная, $Н$ — постоянная Хаббла. Расчёты по данной формуле дают, что $ρ_ <кр>= 10-26\, кг/м^3.$

Критическая плотность — это максимальная плотность вещества Вселенной, которой она якобы может достичь. При достижении максимальной плотности (критической) Вселенная должна перестать расширяться и начать сжиматься. Если плотность меньше критической, то Вселенная продолжит расширяться. По последним оценкам, плотность Вселенной близка к критической (либо немного меньше, либо больше).

6. Опишите модель горячей Вселенной.

Согласно модели, которую выдвинули Ж. Леметр и Г. А. Гамов, на ранних стадиях развития Вселенная имела очень высокую плотность вещества и высокую температуру. Эта гипотеза получила название Большого взрыва.

Суть теории заключается в том, что вселенная возникла в результате взрыва: материя с очень высокой плотностью и огромной энергией начала своё расширение. Такое состояние материи получило название сингулярность — точечный объём с бесконечной плотностью. По мере расширение температура будущей Вселенной постепенно снижалась, что способствовало образованию звёзд и галактик. Хотя процесс образования Вселенной нельзя рассматривать как расширение в окружающее пространство, т.к. его вовсе не было. Вселенная — это всё существующее.

7. Что понимается под закрытой и открытой моделями Вселенной?

Существуют две теоретические модели будущего Вселенной — закрытая и открытая.

Закрытая. Вселенная может быть закрытой системой, которая испытывает множество эволюционных циклов. После цикла расширения Вселенная начнёт процесс сжатия, пока не вернётся в первоначальное состояние — сингулярное — затем снова будет взрыв. Длительность полного цикла составляет 100 млрд лет. Начиная каждый новый цикл, Вселенная теряет «память» и может «родиться» с совершенно новым набором физических констант.

Открытая. Эта модель рассматривает варианты «тепловой смерти» Вселенной. Звёзды в системе постепенно будут остывать и через $10^14$ лет многие их них пропадут, что приведёт к отрыву планет от своих звёзд. Планеты покинут галактики. Сами галактики прекратят своё существование, превратившись в чёрные дыры.

Источник

КРИТИ́ЧЕСКАЯ ПЛО́ТНОСТЬ ВСЕЛЕ́ННОЙ

В книжной версии

Том 16. Москва, 2010, стр. 66

Скопировать библиографическую ссылку:

• 
• 
• 
• 
• 

КРИТИ́ЧЕСКАЯ ПЛО́ТНОСТЬ ВСЕЛЕ́Н­НОЙ, один из осн. па­ра­мет­ров в ре­ше­нии урав­не­ний Фрид­ма­на; зна­че­ние плот­но­сти ве­ще­ст­ва, оп­ре­де­ляе­мое вы­ра­же­ни­ем $ρ_c=3H^2/(8πG)$ , где $H$ – по­сто­ян­ная Хабб­ла, $G$ – гра­ви­тац. по­сто­ян­ная. То­по­ло­гич. свой­ст­ва од­но­род­ной и изо­троп­ной Все­лен­ной с рав­ной ну­лю кос­мо­ло­гич. по­сто­ян­ной за­ви­сят от от­но­ше­ния ср. плот­но­сти Все­лен­ной $ρ$ к К. п. В. Ес­ли $ρ/ρ_c=1$ (ср. плот­ность Все­лен­ной рав­на К. п. В.), то трёх­мер­ное про­стран­ст­во яв­ля­ет­ся евк­ли­до­вым (пло­ским). Ес­ли $ρ/ρ_c (ср. плот­ность Все­лен­ной мень­ше К. п. В.), то трёх­мер­ное про­стран­ство об­ла­да­ет гео­мет­ри­ей Ло­ба­чев­ско­го и ха­рак­те­ри­зу­ет­ся от­ри­ца­тель­ной кри­виз­ной и бес­ко­неч­ным объ­ё­мом. В обо­их слу­ча­ях Все­лен­ная рас­ши­ря­ет­ся бес­ко­неч­но. Ес­ли $ρ/ρ_c>1$ (ср. плот­ность Все­лен­ной боль­ше К. п. В.), то трёх­мер­ное про­стран­ст­во име­ет по­ло­жи­тель­ную кри­виз­ну, яв­ля­ет­ся замк­ну­тым и его объ­ём ог­ра­ни­чен. В та­кой мо­де­ли рас­ши­ряю­щая­ся Все­лен­ная дос­ти­га­ет не­ко­то­ро­го макс. ра­диу­са, а за­тем её рас­ши­ре­ние сме­ня­ет­ся сжа­ти­ем. Ди­на­ми­ка Все­лен­ной, час­тич­но за­пол­нен­ной тём­ной энер­ги­ей (т. е. в слу­чае, ко­гда кос­мо­ло­гич. по­сто­ян­ная не рав­на ну­лю), опи­сы­ва­ет­ся бо­лее ши­ро­ким клас­сом ре­ше­ний. Совр. ис­сле­до­ва­ния по­ка­зы­ва­ют, что зна­че­ние ср. плот­но­сти Все­лен­ной рав­но К. п. В. в пре­де­лах ошиб­ки из­ме­ре­ний.

Источник

Определите значение критической плотности для модели расширяющейся вселенной

§ 7. Будущее расширяющейся Вселенной. Критическая плотность

Расширение Вселенной протекает с замедлением, и для будущего есть две возможности.

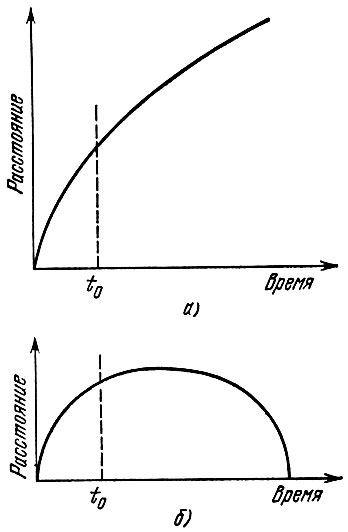
Замедление, как мы видели в § 6, пропорционально плотности вещества во Вселенной. С расширением плотность падает, уменьшается замедление. Возможна ситуация, когда при сегодняшней скорости расширения плотность вещества достаточно мала и замедление мало. Тогда расширение будет протекать неограниченно. На рис. 9,а показан такой случай. Расстояние между любой парой галактик неограниченно возрастает.

Рис. 9. а) Зависимость расстояния между галактиками от времени для плотности вещества во Вселенной меньше критической. Вселенная расширяется неограниченно, б) Такая же зависимость для плотности вещества больше критической Расширение Вселенной сменяется сжатием

Но возможно, что плотность достаточно велика, а значит, велико замедление расширения. В результате расширение прекращается и сменяется сжатием. Изменение расстояния между галактиками в этом случае показано на рис. 9, б.

Ситуация здесь полностью аналогична той, когда ракета, разогнанная до определенной скорости, должна покинуть небесное гело. Так, скорость в 12 км /_сек достаточна, чтобы покинуть Землю и улететь в космос, ибо эта скорость больше «второй космической» скорости для Земли. Однако эта скорость недостаточна для тою, чтобы покинуть поверхность Юпитера, где «вторая космическая» скорость 61 км/сек. На поверхности Юпитера тело, брошенное со скоростью 12 км /_сек вверх, после подъема снова упадет на Юпитер.

Рассмотрим теперь галактику А на границе сферы на рис. 2. Скорость, с которой галактика удаляется от центра О, определяется законом Хаббла v = HR. Если эта скорость больше второй космической для шара радиуса R, то галактика будет неограниченно удаляться от О, Вселенная будет неограниченно расширяться (рис. 9, а), если v меньше второй космической, то расширение сменится сжатием (рис. 9, б). Скорость v = HR определена законом Хаббла и какой случай — 9, а или 9, б — будет иметь место, определяется массой шара, т. е. зависит от плотности ρ.

Итак, для Вселенной при нынешней скорости расширения (сегодняшней постоянной Хаббла 75 км /_сек*Мnс) и при малой плотности характерно неограниченное расширение, при большой плотности — расширение, сменяющееся сжатием. Существует критическое значение плотности вещества ρ_крит отделяющее один случай от другого.

Несложно определить это критическое значение плотности. Действительно, известно, что вторая космическая скорость для шара массы М записывается следующим образом:

Подставляя в (13) выражения для массы 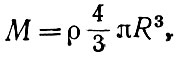, а вместо скорости v = HR, находим

или, выражая отсюда плотность ρ,

Итак, критическое значение средней плотности во Вселенной зависит от постоянной Хаббла Н. При постоянной Хаббла Н = 75 км /_сек*Мnс для ρ_крит получаем

Мы видим, что от величины фактической средней плотности всех видов материи во Вселенной зависит будущая история Вселенной.

Мы уже упоминали кратко в § 6, что для вещества, входящего в галактики, устредненная плотность составляет около ρ_гал = 3*10 -31 г /_{см 3} , т. е. много меньше критического значения ρ_крит. Но, возможно, имеется много трудно наблюдаемого вещества между галактиками. Вопрос этот чрезвычайно важен. В следующих параграфах мы несколько ближе познакомимся с основными структурными единицами Вселенной — галактиками и их скоплениями, — и с проблемой межгалактической материи.

Источник

Космологический принцип. Космологические модели. Масштабный фактор. Критическая плотность Вселенной.

• Космология занимается изучением физических свойств и эволюции Вселенной как целого.

• Современные космологические модели основаны на принципах общей теории относительности, дополненных т. н. космологическим принципом, который для расширяющейся Вселенной гласит: Вселенная однородна и изотропна в каждый момент времени, прошедший после Большого Взрыва.

• Наша Галактика не является избранной, центральной во Вселенной, точно так же, как не являются избранными другие галактики.

• Однородная и изотропная Вселенная не может находиться в стационарном состоянии, из-за наличия сил тяготения, т. е. Такая Вселенная должна или сжиматься или расширяться.

• Однородный шар массы M = Vρ = (4/3)πr3ρ под действием силы гравитации будет сжиматься к центру с ускорением

• Т. о., даже если бы в начальный момент времени некоторая галактика А была неподвижной, то она стала бы двигаться внутрь шара. То же самое касается и других галактик. Поскольку Вселенная однородна и изотропна, такова же будет судьба любого мысленно выделенного объёма, независимо от его размера и местоположения.

• Из-за наличия сил тяготения Вселенная, не обладающая ни центром, ни осью вращения (т. е. однородная и изотропная) не может вечно находиться в одном и том же состоянии, она неизбежно должна эволюционировать.

• При разных начальных условиях эта эволюция может быть разной: Вселенная будет либо расширяться (возможно, с замедлением или ускорением), либо сжиматься (возможно, с ускорением или замедлением).

• Нестационарность Вселенной в принципе могла быть предсказана уже триста лет назад, сразу после открытия закона всемирного тяготения. Этому помешали предубежденность в вечности и неизменности Вселенной.

• В настоящее время Вселенная расширяется, при этом в силу космологического принципа каждая точка пространства Вселенной удаляется от всех остальных её точек.

• Космологические модели, описывающие состояние и эволюцию Вселенной, основаны на решении уравнений тяготения Эйнштейна (по одинаковым верхним и нижним индексам производится суммирование):

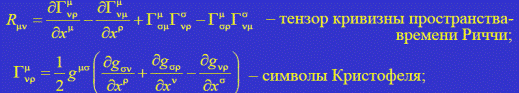
• gμν – метрический тензор; • R = Rνρgνρ – скалярная кривизна (след тензора Риччи); • Tμν – тензор энергии-импульса материи; • μ, ν = 0, 1, 2, 3, где x1, x2, x3 – произвольные пространственные координаты, x0 = ct – временная координата.

• Компоненты метрического тензора gμν определяют квадрат четырёхмерного «расстояния» в пространстве-времени (интервала) ds между двумя бесконечно близкими событиями: ds2 g dxμdxν

• В сферической системе координат интервал имеет вид:

• Параметр k определяет кривизну пространства (–1, 0, +1).

• Тензор энергии-импульса в приближении идеальной жидкости:

где uν—4-вектор скорости жидкости; p—давление жидкости;

ρ— плотность энергии (материи).

• Уравнения Эйнштейна – это система нелинейных дифференциальных уравнений в частных производных

относительно метрического тензора.

• Зная gμν как функции четырёх координат, можно определить все геометрические свойства пространства-

• С помощью метрического тензора вычисляется темп течения времени в различных точках системы отсчёта и

расстояния между точками в трёхмерном пространстве.

• Уравнения тяготения Эйнштейна связывают компоненты метрического тензора gμν с величинами,

характеризующими материю, создающую поле: плотностью, потоками импульса и т.п.

• Первое (стационарное) решение уравнений тяготения было найдено самим Эйнштейном. Впоследствии выяснилось, что такое решение неустойчиво относительно малых возмущений.

• В 1922 году А. Фридман нашёл нестационарное решение уравнений тяготения: А. Фридман. О кривизне пространства, 1922. А. Фридман. О возможности мира с постоянной отрицательной кривизной пространства, 1924.

• Решение Фридмана (в совокупности с современными наблюдательными фактами) утверждает, что в настоящее время Вселенная расширяется.

• Т.о., в прошлом Вселенная была более плотной (более того, бесконечно плотной!). Сценарий будущего Вселенной не настолько однозначен.

• При ограничениях, накладываемых космологическим принципом, уравнения Эйнштейна сводятся к уравнениям Фридмана относительно масштабного фактора:

• Т.к. , то после деления второго уравнения на H2:

• Величина называется параметром плотности.

• При Ω 1 кривизна пространства положительна (k = +1 м–2). • При Ω = 1 кривизна пространства равна нулю (k = 0).

• Значение плотности энергии, при котором Ω = 1 называется критической плотностью:

Критическая плотность Вселенной

• Выводы из теории Фридмана относительно будущего существенно зависят от соотношения между сегодняшними значениями постоянной Хаббла и средней плотности вещества во Вселенной.

• Существует определённая критическая величина плотности, которая и будет определять дальнейший сценарий эволюции.

• Эта плотность определяется величиной скорости убегания uII (второй космической скорости) с поверхности однородного шара:

• Если при этом исходная скорость объекта (галактики) v = uII, то на бесконечности эта скорость стремится к нулю, а если v > uII, то — к некоторой ненулевой величине.

Сценарий будущего и параметры Вселенной при ρ uII),

то тяготение не сможет остановить расширение.

• Хотя расширение и будет замедляться, но оно не сменится сжатием.

• При этом пространство бесконечно, а при однородной плотности бесконечно и общее количество

вещества во Вселенной.

• Геометрия пространства неевклидова, а кривизна отрицательна.

Сценарий будущего и параметры Вселенной при ρ = ρ_c

• При средней плотности, равной критической ρ = ρc (т. е. v = uII), скорость расширения стремится к нулю (происходит замедление расширения), кривизна пространства равна нулю, и

пространство в среднем обладает евклидовой геометрией.

Сценарий будущего и параметры Вселенной при ρ > ρ_c

• Если же плотность больше критической ρс: ρ > ρc (т. е. v

Источник