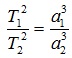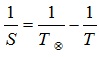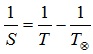ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Все мы гении. Но если вы будете судить рыбу по её способности взбираться на дерево, она проживёт всю жизнь, считая себя дурой.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
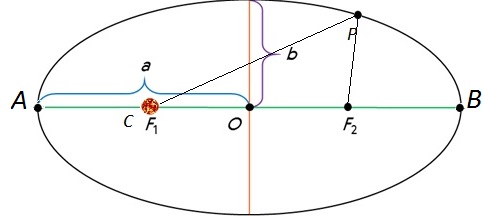
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
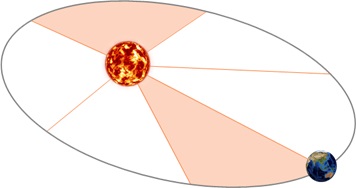
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
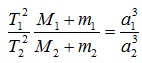
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
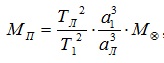
где Тл и α л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Источник
Урок 8
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
Перигелийное расстояние $ПС = q$; афелийное расстояние $СА = Q$. $АП = 2a$; $ПО = ОА = a$. Тогда: $q = ОП — СО$; $e = \dfrac<СО><ОП>$; $СО = e · a$; $Q = ОА + СО$; $q = a — ea = a(1 — e)$; $Q = a + ea = a(1 + e)$.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
- а) скорость планеты максимальна;
- б) потенциальная энергия максимальна;
- в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
- а) скорость планеты минимальна;
- б) потенциальная энергия минимальна;
- в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник
Определить период обращения Юпитера вокруг Солнца
3. Согласно 3-му закону Кеплера между периодами вращения
Т, их массами m и большими полу-орбитами a существует такое
coотношение: T1^2(M+m1) / T2^2(M+m2) = a1^3 / a2^3
Здесь М — масса Солнца. Земля
вращается вокруг Солнца на расстоянии а1 = 150 000 000 км (1 астрономическая единица), её период вращения Т1 = 1 год, а отношение
массы Земли к массе Солнца m1/M = 3,02 * 10^-6. Юпитер, у которого m2/M =9,55 * 10^-4, вращается на расстоянии а2 = 5.2 астр. ед. Определить период
обращения Юпитера вокруг Солнца в годах и расстояние а2 в км. Работать с
числами в формате плавающей точки.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Создать модель движения Солнца вокруг орбиты, Земли вокруг Солнца, Луны вокруг земли
Вот есть набросок, что дальше? :help: Const pi = 3.14 Dim intRev As Single Private Sub.
Найти период обращения звезд вокруг общего центра масс
3) Звездная система состоит из двух одинаковых звезд, находящихся на расстоянии r=5*10^11 м друг от.
определить период обращения шарика
Шарик, подвешенный на невесомой нерастяжимой нити, равномерно движется по окружности, расположенной.
Определить период обращения электрона.
Электрон движется в однородном магнитном поле с индукцией В= 9 мТл по винтовой линии, радиус.
Вращение планеты вокруг солнца, и вокруг своей оси
У меня есть Солнце, которое находиться в координатах(0.0.0), и нужно вращать планеты, как по.

2) Разработайте динамическую модель Земли, которая вращается вокруг Солнца и вокруг которой.

надо в паскале написать программу которая графически изобразит движение Луны вокруг Земли а .
Сделать анимацию вращения Земли вокруг Солнца одновременно с анимацией вращения Луны вокруг Земли
помогите сделать анимацию вращения земли вокруг солнца одновременно с анимацией вращения луны.

Помогите пожалуйста написать код Создать графическую анимацию с пейзажем. -Полнота анимированной.
Светящийся эффект вокруг солнца
Как сделать эффект свечения, на directx 9
Источник
Астрономия. Решение задач. Тема: Законы Кеплера
Из опыта работы
Тема : Законы Кеплера
Звездный период обращения Юпитера вокруг Солнца составляет около 12 лет. Каково среднее расстояние Юпитера от Солнца?
Среднее расстояние планеты от Солнца равно большой полуоси эллиптической орбиты a. Из третьего закона Кеплера


для определения среднего расстояния планеты от Солнца в астрономических единицах по известному звездному (сидерическому) периоду обращения, выраженному в годах. Подставив численные значения окончательно найдем:

Ответ: около 5 а.е.
Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а=2,88 а. е., а эксцентриситете =0,24
а=2,88 а.е
е=0,24
_________________________
Радиус перигелия рассчитывается по формуле: r=(1-e)а, где: a — большая полуось; е — эксцентриситет орбиты.
Афелий орбиты рассчитывается по формуле r =(1+е)а, где a — большая полуось; е — эксцентриситет орбиты.
r=2.88(1 +0,24)=3.57 а.е
Ответ: 3.57 а.е
Период обращения малой планеты Шагал вокруг Солнца Т=5,6 года. Определите большую полуось ее орбиты.

а1=Т1 2
а1=3√5,6 2 =3.2 а.е
Ответ: 3.2 а.е
Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а=160 млн км, а эксцентриситет е=0,83.
а = 160 млн. км
е = 0,83
_________________________
r=?
r=(1-e)а
r=1,6*10 8 (1-0,83)=2,72*10 7 км
Ответ: 2,72*10 7 км
просмотров всего 64,022 , просмотров сегодня 28
Источник
Период обращения юпитера вокруг солнца задача
Рассмотрите таблицу, содержащую некоторые характеристики планет Солнечной системы. Размеры и параметры орбит даны в сравнении с планетой Земля.
| Имя | Диаметр | Масса | Орбитальный (земных суток) | ||
|---|---|---|---|---|---|
| Нептун | 3,9 | 17,2 | 30,1 | 165 | 0,67 |
| Уран | 4 | 14,6 | 19,2 | 84 | 0,72 |
| Сатурн | 9,5 | 95,2 | 9,5 | 29,5 | 0,43 |
| Юпитер | 11,2 | 318 | 5,2 | 11,9 | 0,41 |
| Марс | 0,53 | 0,11 | 1,5 | 1,9 | 1 |
| Земля | 1 | 1 | 1 | 1 | 1 |
| Венера | 0,95 | 0,82 | 0,72 | 0,62 | 243 |
| Меркурий | 0,38 | 0,06 | 0,39 | 0,24 | 58,6 |
Выберите два утверждения, которые соответствуют характеристикам планет.
1) Средняя плотность Венеры меньше средней плотности Земли.
2) Центростремительное ускорение Юпитера при его вращении вокруг Солнца больше центростремительного ускорения Марса.
3) Первая космическая скорость для Нептуна меньше, чем для Урана.
4) Ускорение свободного падения на Меркурии составляет примерно 4 м/с 2 .
5) Сила притяжения Сатурна к Солнцу больше, чем у Юпитера.
1) Средняя плотность планеты Отношение средней плотности Венеры к средней плотности Земли
меньше единицы. Значит, средняя плотность Венеры меньше средней плотности Земли.
Утверждение 1 верно.
2) Центростремительное ускорение планеты Юпитер расположен дальше от Солнца, чем Марс, поэтому центростремительное ускорение Юпитера при его вращении вокруг Солнца меньше центростремительного ускорения Марса.
Утверждение 2 неверно.
3) Первая космическая скорость Масса Нептуна больше массы Урана, а радиус Нептуна меньше радиуса Урана, значит, первая космическая скорость для Нептуна больше, чем для Урана.
Утверждение 3 неверно.
4) Ускорение свободного падения на планете Ускорение свободного падения на Меркурии по отношению к земному
И, значит,
Утверждение 4 верно.
5) Сила притяжения планеты к Солнцу Масса Сатурна меньше массы Юпитера и Сатурн расположен дальше от Солнца, чем Юпитер, поэтому сила притяжения Сатурна к Солнцу меньше, чем у Юпитера.
Источник