Дж. Дарвин создает теорию приливной эволюции системы Земля — Луна
Явление приливов, понятое и объясненное уже Ньютоном (см. здесь с. 75), очень сложно в силу существования материков и островов разных очертаний, разной глубины океанов, имеющих сложный рельеф дна, и многих других причин. Да и вызывающие приливы Луна и Солнце занимают разное положение по отношению к Земле, вследствие чего они действуют то в одном направлении, усиливая приливы, то в противоположном, ослабляя их. Важно иметь в виду то обстоятельство, что в то время как силы притяжения меняются обратно пропорционально квадрату расстояния между небесными телами, приливная сила, т.е. разность притяжений к светилу и центру Земли, в первом приближении меняется обратно пропорционально кубу расстояния между телами.
Приливы происходят и в теле самой Земли, недра которой — горячая магма, раскаленное ядро и даже земная кора — обладают некоторой вязкостью. Сейсмографы обнаруживают приливы в Земле, хотя и с меньшей амплитудой, чем у приливов в океанах. Между водой океана и его дном есть трение. Оно вызывает запаздывание приливов (по сравнению с предсказаниями имевшейся теории приливов), доходящее до 6 часов, при промежутке между приливами около 12 часов.
Дж. Дарвин (сын великого биолога Ч. Дарвина) показал в конце 80-х годов XIX в., что вследствие приливного трения Луна от нас удаляется, одновременно замедляя свое вращение вокруг оси (но этой причине она и обращена теперь к Земле одной стороной). Но замедляется и вращение Земли. Это будет продолжаться до тех пор, пока и на Земле сутки, наконец, не сравняются по своей длине с месяцем (т. е. с периодом обращения Луны), который тоже удлиняется, но гораздо медленнее. Конечно, это происходит при условии, что посторонние силы не вмешиваются в приливную эволюцию системы. Месяц и сутки, по расчетам, станут оба равны 1400 часам или, по другим данным, 11 240 часам (в зависимости от величины трения солнечного прилива). Тогда будет достигнуто положение «приливного равновесия» системы Земля — Луна.
Действительно, удлинение суток подтвердилось при сравнении моментов затмений Солнца, отмеченных в старинных хрониках, с найденными путем современных вычислений их «назад». Кроме того, современные точнейшие часы — кварцевые и атомные — обнаруживают даже кратковременные, более мелкие, колебания скорости вращения Земли, также связанные отчасти с приливным трением. Дарвин рассмотрел эту историю, дойдя до момента, когда Луна обращалась вокруг Земли за время от 2 до 4 часов, при этом почти касаясь Земли, имевшей сутки такой же длительности.
Но такое положение равновесия, при котором не действуют приливные силы, не могло быть устойчивым. Малейшее возмущение и изменение скорости орбитального движения Луны должно было вызвать ряд перемен: Луна либо упала бы на Землю, либо стала отдаляться от нее. Из наблюдаемой ныне картины ясно, что случилось второе. Дарвин не давал в своей строгой математической теории определенного ответа на вопрос о том, как именно произошла Луна. Вместе с тем он подсчитал, что взаимное удаление Земли и Луны должно было начаться 54·10 6 лет тому назад или несколько ранее.
Вслед за Дж. Дарвином большой вклад в построение теории вращения одиночного симметричного жидкого тела внесли русский механик А.М. Ляпунов, французский математик и небесный механик А. Пуанкаре и особенно английский физик и астрофизик Дж. Джинс, приложивший эту теорию к различным космическим объектам. Они изучали условия равновесия однородных и неоднородных симметричных фигур и установили возможность превращения их в грушевидные (Дарвин), в подобие гантелей и даже в фигуры с двумя перехватами (Джинс).

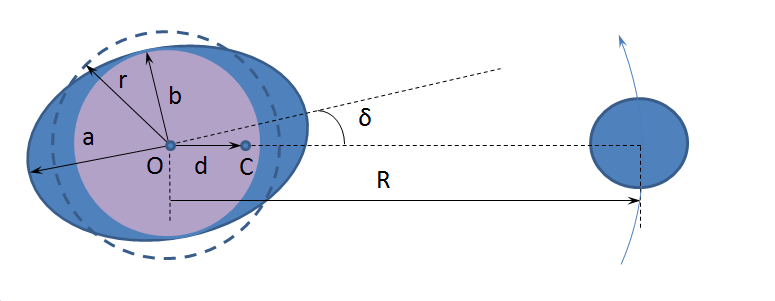
Рис. 11. Эволюция системы Земля — Луна по Дж. Дарвину
Все они приходили к выводу, что при дальнейшем увеличении угловой скорости вращения этих, например грушевидных, фигур перемычка утончается и такие тела могут распасться. Конечно, вывод о возможности распада такого тела еще не означает, что двойная система Земля — Луна возникла именно при таком катастрофическом распаде, хотя некоторые до сих пор думают, что громадная впадина Тихого океана и есть то место, где произошел разрыв системы. Вместе с тем, обнаруженное отклонение формы Луны от шара (некоторые находят сходство ее с яйцом), причем ее вытянутость направлена «острием» к Земле, есть, несомненно, следствие приливов: «острие», или горб Луны, и есть «застывший прилив».
Вскоре выяснилось, что вращение и приливное трение недостаточны для описания эволюции Солнечной системы. Почему-то у Венеры и Меркурия спутников нет, хотя расстояние Венеры от Солнца, ее масса, размер, наличие плотной атмосферы, казалось, делали ее очень сходной с Землей. Марс имеет два крохотных спутника, приливное воздействие которых на планету ничтожно мало.
Новый интерес к идее приливной эволюции возник в наши дни. Открытый недавно (в 1978 г.) спутник Плутона (Харон) столь близок к нему (и сравним с ним по размерам), что фаза приливной эволюции этой системы, вероятно, критическая. В истории этой пары приливное трение должно было играть большую роль. Но никаких расчетов по этому поводу автор в литературе до сих пор не встречал. По новым данным, Харон, открытый через полвека после открытия самой планеты, отстоит от нее на 20000 км, имеет диаметр около 1300 км, а Плутон имеет диаметр немногим более 3000 км. Значит, промежуток между поверхностями планет составляет около 18000 км, т. е. эта система существенно более тесная, чем в случае Земли и Луны.
До сих пор наша планета со своим спутником резко выделялась в Солнечной системе тем, что ни у одной другой планеты не было такого большого спутника в сравнении с ней. Масса Луны всего в 81 раз меньше земной массы, а диаметр меньше земного только в 4 раза, расстояние же между ними равно 60 радиусам Земли. Теперь же эта исключительность утрачена.
Период обращения Харона около 6,4 земных суток и, видимо, равен периоду вращения Плутона. Следовательно, Харон «висит» всегда над одной и той же точкой поверхности Плутона — положение, которое теория Дарвина предсказывала раньше для начальной фазы истории Земли и Луны вскоре после рождения последней. Итак, новые открытия показывают применимость теории Дарвина не только к системе Земля — Луна. Открылась возможность лучшего соспоставления теории Дарвина с наблюдениями. По аналогии с теоретической историей Земли и Луны можно было бы думать, что в космической шкале времени Харон лишь недавно отделился от Плутона.
В отношении внутренних планет, Меркурия и Венеры, их крайне медленное осевое вращение, несомненно, обусловлено приливами, которые в них вызывало Солнце. Ведь у Меркурия период его осевого вращения, 58 суток (что было установлено лишь в 1965 г. радиоастрономическими методами), составляет ровно 2/3 от периода его обращения вокруг Солнца (88 суток). Так что за 176 земных суток Меркурий делает три оборота по отношению к звездам, два витка по орбите и только один оборот относительно Солнца. Солнечные приливы там в 15 раз более сильные, чем для Земли, и именно они затормозили вращение Меркурия вокруг оси, доведя его солнечные сутки до 176 земных.
На Венере же солнечные сутки равны 584 земным. Поэтому приливная волна на Венере перемещается сейчас крайне медленно и за миллионы лет затормозила ее вращение еще сильнее, чем на Меркурии. А то обстоятельство, что Венера, по-видимому, обращена к Земле всегда одной и той же стороной, вызвано, может быть, земными приливами на Венере, хотя расстояние между этими двумя планетами составляет 30 млн. км при наибольшем их сближении.
Влияние же приливов на планеты-гиганты даже со стороны крупнейших спутников из-за сравнительной малости масс последних очень незначительно. Оно и очень сложно, потому что крупных спутников несколько и расположение их относительно планеты и друг друга все время меняется. Иногда приливные действия их взаимно противоположны.
На ближайшем к Юпитеру (из галилеевых) спутнике Ио, как уже упоминалось, пролетающие космические аппараты зафиксировали с полдюжины действующих вулканов. По одной из гипотез, причиной их активности могут быть приливы в разогретой магнитными процессами магме.
Источник
Приливное трение эволюция системы земля луна
Приливная эволюция системы Земля-Луна, происходит по причине передачи момента импульса быстро вращающейся Земли орбитальному движению Луны посредством гравитационно-приливного взаимодействия. Приливный горб, деформирующий поверхность Земли оседает не сразу, выходя из подлунной точки, а некоторое время тянет Луну за собой, разгоняя ее на орбите и притормаживая вращение Земли.
Рассчитаем момент импульса системы Земля-Луна (СЗЛ), полагая, что оба тела движутся по круговым орбитам, ось вращения Земли перпендикулярна плоскости ее орбиты. Луне принадлежит часть момента импульса:
$L_m=M_m (R-d)^2 \Omega$, (1)
где $M_m$ — масса Луны, $R$- расстояние между центрами Земли и Луны, $d$ — расстояние от центра Земли до барицентра СЗЛ, равное
$\Omega$ — угловая скорость вращения СЗЛ вокруг ее барицентра, которая равна
где $M_e$ — масса Земли, $G$ — гравитационная постоянная.
В итоге, момент импульса Луны в ее движении по орбите равен:
Поскольку суммарный момент импульса СЗЛ сохраняется, изменение момента импульса Луны зависит от приливного момента, действующего на Землю, взятого с обратным знаком:
В работе [1] было показано, что приливный момент, тормозит вращение Земли:
где $m$ — точечная масса, сосредоточенная в вершине приливного горба, создающая момент, равный реально действующему, $r$ — радиус Земли, $ \delta $ — смещение приливного горба относительно подлунной точки.
В результате приливного взаимодействия уровенная поверхность Земли принимает форму эллипсоида вращения[2], полуоси которого равны:
Результирующий приливный момент определяется массой, находящейся за пределами сферы радиуса $b$. Масса приливного горба, таким образом, равна
где $\rho$ — плотность вещества приливного горба, $\Delta V$ — разность объемов приливного эллипсоида и сферы радиуса $b$.
Точечная масса, сосредоточенная в вершине приливного горба, создающая момент, равный реально действующему, очевидно меньше массы всего приливного горба и равна:
где $k_m Войдите на сайт для отправки комментариев
Источник
Будущее системы Земля — Луна
В эпоху своего возникновения Луна находилась в несколько раз ближе к Земле, чем теперь, и гораздо быстрее вращалась вокруг своей оси. Гравитационное притяжение соседней Земли вызывало па расплавленной поверхности лунного шара сильные приливы. Под их воздействием Луна приняла несколько вытянутую форму, а когда она затвердела, форма ее так и осталась вытянутой.
Приливное трение постепенно замедляло скорость вращения Луны. Это происходило до тех пор, пока период вращения Луны вокруг оси не стал равен периоду ее обращения по орбите вокруг Земли. И теперь нам видна только одна сторона Луны.
Поскольку масса Земли в 81 раз больше массы Луны, то приливная сила, оказываемая Землей на Луну, гораздо больше, чем приливная сила, оказываемая Луной на Землю. Как известно, волны лунных приливов, надвигаясь каждый раз на восточные берега земных материков, создают силу приливного трения водных масс о твердое тело нашей планеты. В результате Земля замедляет свое вращение, а продолжительность суток постепенно возрастает. При сохранении скорости увеличения длины суток на 1,5 секунды за 100 тыс. лет уже в текущем геологическом периоде (через 10 млн лет) в земном году будет на одни сутки меньше.
Приливное взаимодействие в системе Земля—Луна приводит еще к тому, что наш спутник отходит от Земли все дальше и дальше. Вычисления показали, что это будет происходить до тех пор, пока продолжительность лунного месяца и земных суток не сравняются и не достигнут примерно 50—55 теперешних суток. Луна будет тогда находиться от Земли раза в полтора дальше, чем теперь, то есть примерно па расстоянии 600 тыс. км.
Приливная эволюция системы Земля—Луна совершается также под влиянием притяжения Солнца, но гораздо медленнее. Так, в результате приливного воздействия центрального светила период вращения нашей Земли должен увеличиваться до тех пор, пока он не станет равным годичному периоду обращения Земли. В таком положении, возможно, окажется планета Меркурий.
Постепенное удлинение земных суток вследствие солнечных приливов нарушит установившееся относительное равновесие в системе Земля—Луна. Луна станет приближаться к Земле. Расчеты показывают, что через многие миллиарды лет это сближение должно завершиться катастрофой.
Можно подумать, что Лупа упадет на Землю, но до этого дело, видимо, не дойдет. Просто, когда Луна приблизится к Земле на запретное расстояние — достигнет так называемого предела Роша, ближе которого она не может сохранить устойчивую форму, наш естественный спутник будет разорван на части мощными земными приливными силами. Из множества лунных фрагментов вокруг Земли возникнет кольцо, похожее на кольцо Сатурна. Разрыв Луны произойдет примерно тогда, когда расстояние между центрами двух небесных тел (Земли и Луны) сократится до 18 тыс. км.
Восстановление эволюционного пути Луны проливает свет па ряд спорных моментов в прошлом и позволяет заглянуть в будущее Земли.
Источник
Начала физики. 20. Приливные силы и эволюция системы Земля-Луна.
Приливные силы — это разность гравитационных сил притягивающего тела на «концах» притягиваемого тела. Они растягивают оба тела вдоль прямой, соединяющей центры масс этих тел. Земля растягивает Луну, а Луна, в свою очередь, растягивает Землю. Этот эффект на Земле мы наблюдаем в виде дважды в сутки набегающих на берега океанов приливов и последующих отливов.
1. Приливные силы.
Получить закон приливного тяготения просто. Рассмотрим систему планета-спутник с планетой массы М и радиуса R 0 и спутником массы m и радиуса R 1 , обращающемся вокруг планеты. Для простоты рассуждений будем считать планету Землей, а спутник — Луной. Если расстояние между центрами планеты и спутника есть r, то действующая со стороны планеты на спутник приливная сила есть
F зл = GmM/(r — R 1 ) ² — GmM/(r + R 1 ) ², (1)
а действующая со стороны спутника на планету приливная сила есть
F лз = GmM/(r — R 0 ) ² — GmM/(r + R 0 ) ². (2)
Мы видим, что эти выражения отличаются только размером (радиусом) притягиваемого тела.
Заметим, в случае системы Земля-Луна r >> R 0 и r >> R 1 . Будем считать эти соотношения стандартом, то есть не будем рассматривать слишком близкие друг к другу планету и спутник. Тогда выражения (1) и (2) можно разложить в ряд Тэйлора по малым параметрам r/ R 0 и r/ R 1 и в первом приближении по этим малым параметрам отношений радиусов планеты и спутника к расстоянию между их центрами выражения (1) и (2) можно заменить на:
F зл ≈ 4GMm R 1 /r ³, (3)
F лз ≈ 4GMm R 0 /r ³, (4)
Откуда видно, что приливные силы обратно пропорциональны кубу расстояния между небесными телами и пропорциональны размеру притягиваемого тела.
2. Что творят эти приливные силы?
Поскольку небесные тела не абсолютно тверды, то приливные силы растягивают их вдоль линии, соединяющие их центры. А поскольку они не абсолютно упруги, то деформация растяжения приводит к диссипации энергии в их недрах. Вдобавок, если эти тела вращаются вокруг своих осей и периоды таких вращений не совпадают с их орбитальными периодами (как ныне у Луны), то их растяжение бежит по недрам и поверхности тел с угловой скоростью, равной разности угловых скоростей орбитального и собственного (вокруг своей оси) вращений. В результате деформация растяжения сменяется деформацией сжатия тела с частотой, равной разности угловых скоростей орбитального и собственного вращений. Что приводит к непрерывной диссипации энергии вращения небесного тела.
Эта диссиппация энергии уменьшает момент импульса вращения небесного тела вокруг своей оси. В случае достаточно малых тел (спутники планет) этот процесс завершается синхронизацией орбитального периода с периодом вращения вокруг своей оси за достаточно малое по космологическим меркам времени. Именно это произошло с Луной, Галилеевыми спутниками Юпитера и еще рядом спутников планет солнечной системы. И факт завершения этого процесса называют приливным захватом спутника. В этом случае приливной горб на спутнике, ориентированный по линии, соединяющей планету и спутник, стоит на месте, деформация спутника стационарна и диссипация энергии прекращена.
Приливные силы взаимны. Поэтому Луна растягивает Землю в направлении на себя. Но Земля вращается вокруг своей оси гораздо быстрее, чем Луна вокруг нее. И поэтому деформация растяжения (приливной горб) бежит по Земле и совершает оборот примерно за сутки (приливных горба — два, один на стороне Луны, другой — на противоположной стороне). Периодическая деформация тела Земли из-за диссипации ее энергии замедляет вращение Земли вокруг своей оси. Но из-за существенной разницы в массах Земли и Луны этот процесс идет чрезвычайно медленно. Насколько?
По последним геологическим данным примерно 1,4 миллиарда лет назад длительность земных суток составляла 18,7 нынешних земных часов, а не 24 часа, как сейчас. Другими словами — длительность земных суток убывает на один час примерно за 265 миллионов лет. А поскольку история Земли как небесного тела насчитывает примерно 4,5 млрд. лет, то в начале своей истории (оценка по грубой линейной аппроксимации) длительность земных суток составляла около 7 нынешних земных часов.
Вдумчивый студент сразу заметит — «Простите, момент импульса вращения Луны вокруг своей оси уменьшился до некоей минимальной величины, момент импульса вращения Земли вокруг своей оси продолжает уменьшаться, но система Земля-Луна является замкнутой в том смысле, что в окружающем эту систему пространстве нет тормозящих ее вращение сил. Значит, и момент импульса этой системы должен сохраняться! Куда же он девается?«
Задав такой вопрос этот студент неявно на него и ответил. Момент импульса системы Земля-Луна должен сохраняться. Но убыль момента импульса из вращательных движений Земли и Луны вокруг их осей должна полностью компенсироваться прибылью момента импульса в орбитальном движении Луны вокруг Земли. Другими словами, радиус орбиты Луны должен непрерывно увеличиваться. И астрономические наблюдения последних лет полностью подтверждают этот вывод — радиус орбиты Луны увеличивается темпом в 3,9 сантиметра в год. А полный момент импульса системы Земля-Луна, действительно, сохраняется.
Есть еще один вопрос. А каковы действующие на Землю приливные силы от Солнца и какова их роль? Да, Солнце почти в 27 млн. раз массивней Луны, но зато почти в 400 раз дальше Луны. И если масса входит в выражение приливной силы линейно, то расстояние — в третьей степени. Надо, очевидно, посчитать. Расчет для средних расстояний Солнца и Луны от Земли показывает, что действующие на Землю приливные силы от Солнца оказываются чуть меньше половины приливных сил от Луны. Поэтому приливы в земных океанах, когда Солнце, Земля и Луна выстраиваются вдоль одной прямой, оказываются максимальными.
Источник