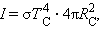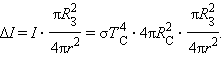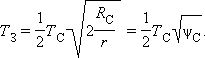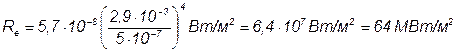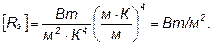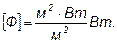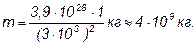Солнечная постоянная $C$, по определению, есть величина, равная:

где $W$ — энергия, излучаемая Солнцем за время $t$; $S = 4 \pi r^<2>$ — площадь сферической поверхности, радиуса $r$ который равен среднему расстоянию Земли от Солнца.
Энергию, излучаемую Солнцем за время $t$ выразим следующим образом

где $R_$ — излучательность Солнца, т.е. энергия, которую оно излучает в единицу времени единицей поверхности; $S_<0>$ — площадь поверхности Солнца.
Подставляя выражение (2) в формулу (1) получаем

Выразим площадь поверхности Солнца $S_<0>$ через диаметр $d$ по формуле: $S_ <0>= \pi d^<2>$. Тогда,

Обратимся к рисунку. Так как угол $\theta$ мал, то можно записать, что $d = r \theta$, где угол $\theta$ выражаем в радианах. С учетом этого формула (3) принимает вид:

Отсюда определяем излучательность Солнца

Температуру поверхности Солнца определим воспользовавшись законом Стефана- Больцмана, полагая, что Солнце излучает как абсолютно черное тело.
Согласно закону Стефана — Больцмана излучательность абсолютно черного тела

где $\sigma$ — постоянная Стефана — Больцмана ($\sigma = 5,67 \cdot 10^ <-8>\frac<Вт> <м^<2>\cdot К^ <4>>$ ). Отсюда

Подставляя в это выражение значение $\sigma$ и найденное выше значение $R_$ и произведем вычисления, получим:

Источник

Принимая что солнце излучает как абсолютно черное тело вычислить его энергетическую светимость

Задача 539. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

Пример 2. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Мe Солнца; 2) поток энергии Фe, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.

Задачи для самостоятельного решения:

1. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость ослабла в 16 раз.

2. Температура внутренней поверхности муфельной печи при при открытом отверстии площадью равна Т. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая мощность составляет Р.

3. Определить, как и во сколько раз изменится излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с л1 до л2

4. Площадь, ограниченная графиком спектральной плотности энергетической светимости r(л,Т) черного тела, при переходе от термодинамической температуры Т1 к температуре Т2 увеличилась в 5 раз. Определить, как изменится при этом длина волны лmax, соответствующая максимуму спектральной плотности энергетической светимости черного тела.

5. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилось с л1, до л2. Определить, во сколько раз увеличилась: 1). энергетическая светимость тела; 2). максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает по закону (r(л,Т))max=СТ^5, где С извесная постоянная величина.

6. Определить, какая длина волны соответствует максимальной спектральной плотност энергетической светимости (r(л,Т))max (С – постояннай в законе, связывающем максимальную спектральную плостность энергетической чветимости черного тела с термодинамической температурой и равна 1,3*10^(-5) Вт(м^3*K^5). 7. Считая никель черным телом, определите мощность, необходимую для поддержания температуры расплавленного никеля t неизменной, если площадь его поверхности равна S. Потерями пренебречь

8. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответстует длина волны л, определить: 1). температуру поверхности Солнца; 2). энергию, излучаемую Солнцем в виде электромагнитных волн за время t; 3) массу, теряемую Солнцем за это время за счёт излучения.

9. Определить темепратуру тела, при которой оно при температуре окружающей среды t0 излучало энергии в n раз больше чем поглощало.

10. Считая, что тепловые потери обусловлены только излучением, опеределите, какую мощность необходимо подводить к медному шарику диаметром d, чтобы при температуре окружающей среды t0 поддерживать его температуру равной t. Примите поглощательную способность меди Аr.

11. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d, температура которой в вакууме поддердивается постоянной и равной t. Поверхность проволоки считать серой с поглощательной способностью Ar. Удельное сопротивление проволоки при данной температуре ро. Температура окружающей проволоку среды t0

12. Используя формулу Планка, определите спектральную плотность потока излучения еденицы поверхности черного тела, приходящегося на узкий интервал длин волн дл около максимума спектральной плотности энергетической светимости, если температура черного тела T.

13. Для вольфрамовой нити при температуре T поглощательная способность Ar. Определить радиационную температуру нити.

14. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0.

Источник

Задачи с решениями

Принимая, что Солнце излучает как абсолютно черное тело с температурой поверхности , оцените среднюю температуру земной поверхности в предположении, что Земля также является абсолютно черным телом, а роль тепловых процессов внутри Земли пренебрежимо мала. Угловой диаметр Солнца, видимый с Земли, примите равным .

В пренебрежении процессами, идущими в недрах Земли, тепловой баланс Земли определяется поглощением энергии солнечного излучения и собственным излучением в пространство. Полный поток энергии , излучаемой Солнцем по всем направлениям, в соответствии с законом Стефана–Больцмана равен

где – постоянная Стефана–Больцмана, – радиус Солнца. Часть полного потока падает на поверхность Земли и поглощается:

Здесь – радиус Земли, – расстояние от Земли до Солнца.

Такой же поток энергии Земля должна излучать в пространство, иначе ее температура не будет оставаться постоянной. Приравнивая поток излучаемой Землей энергии 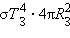и поглощаемый ею поток энергии , получим:

Из этого выражения видно, что для определения нужно знать только температуру поверхности Солнца и его угловой диаметр 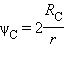. Числовой расчет дает значение . Этот результат весьма близок к реальному значению средней температуры поверхности Земли.

Источник

Пример 31

Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны l » 5000 ангстрем. Принимая Солнце за абсолютно черное тело, определить: 1) энергетическую светимость Солнца; 2) поток энергии, излучаемой Солнцем; 3) массу электромагнитных волн (всех длин), излучаемых Солнцем за одну секунду.

Дано: Решение

l » 5 . 10 -7 м 1. Энергетическая светимость R_э абсолютно черного

Ф,R_э, m = ? тела выражается формулой Стефана-Больцмана:

где s — постоянная Стефана-Больцмана; Т – абсолютная температура излучающей поверхности.

Температура может быть определена из закона смещения Вина:

где l₀ — длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела; b – постоянная Вина.

Выразив из закона смещения Вина температуру Т и подставив ее в формулу (1), получим:

(2)

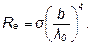
Подставив числовые значения в выражение (2) и произведя вычисления, получим:

2. Поток энергии Ф, излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности:

где r – радиус Солнца.

Подставив числовые значения в формулу (3), найдем:

Ф = 4 . 3,14 . (7 . 10 8 ) 2. ×6,4 . 10 7 Вт = 3,9×10 26 Вт.

3. Массу электромагнитных волн (всех длин), излучаемых Солнцем за 1 с определим, применив закон пропорциональности массы и энергии:

Энергия электромагнитных волн, излучаемых за время t, равна произведению потока энергии (мощности излучения) на время

Следовательно, Фt = mc 2 , откуда m = Фt/c 2 .

Сделав подстановку числовых значений величин, найдем:

.

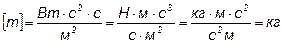
Источник

Принимая что солнце излучает как абсолютно черное тело вычислить его энергетическую светимость

Средняя энергетическая светимость R поверхности Земли равна 0,54 Дж/(см 2 •мин). Какова должна быть температура T поверхности Земли, если условно считать, что она излучает как серое тело с коэффициентом черноты a_T = 0,25?

Металлическая поверхность площадью S = 15 см 2 , нагретая до температуры T = 3 кК, излучает в одну минуту 100 кДж. Определите: 1> энергию, излучаемую этой поверхностью, считая ее черной; 2) отношение энергетических светимостей этой поверхности и черного тела при данной температуре.

Показать с помощью формулы Вина, что: а) наиболее вероятная частота излучения ω_вер

T; б) максимальная спектральная плотность теплового излучения (u_ω)_макс

Т 3 ; в) энергетическая светимость М_э

Поверхность тела нагрелась до температуры 1000 К. Затем одну половину этой поверхности нагрели на 100 К, другую охладили на 100 К. Во сколько раз изменилась энергетическая светимость поверхности этого тела?

Какое количество энергии излучает 1 см 2 затвердевающего свинца в 1 с? Отношение энергетических светимостей поверхности свинца и абсолютно черного тела для этой температуры считать равным 0,6

Какую энергетическую светимость R’_э имеет затвердевающий свинец? Отношение энергетических светимостей свинца и абсолютно черного тела для данной температуры k = 0,6.

Мощность излучения раскаленной металлической поверхности N’ = 0,67 кВт. Температура поверхности T = 2500 К, ее площадь S = 10 см 2 . Какую мощность излучения N имела бы эта поверхность, если бы она была абсолютно черной? Найти отношение k энергетических светимостей этой поверхности и абсолютно черного тела при данной температуре.

Диаметр вольфрамовой спирали в электрической лампочке d = 0,3 мм, длина спирали l = 5 см. При включении лампочки в сеть напряжением U = 127 В через лампочку течет ток I = 0,31 А. Найти температуру T спирали. Считать, что по установлении равновесия все выделяющееся в нити тепло теряется в результате излучения. Отношение энергетических светимостей вольфрама и абсолютно черного тела для данной температуры k = 0,31.

Определить температуру Т, при которой энергетическая светимость M_e черного тела равна 10 кВт/м 2 .

Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела λ₀ = 0,58 мкм. Определить энергетическую светимость (излучательность) R_e поверхности тела.

Температура тела при нагревании изменилась от температуры Т₁ = 1000 К до Т₂ = 3000 К. Во сколько раз увеличилась при этом энергетическая светимость тела? На сколько изменилась длина волна, на которую приходится максимум излучения?

Принимая, что Солнце излучает как черное тело, вычислить его энергетическую светимость M_e и температуру Т его поверхности. Солнечный диск виден с Земли под углом θ = 32′. Солнечная постоянная С = 1,4 кДж/(м 2 ·с).

Во сколько раз отличаются термодинамические температуры и энергетические светимости участков тела человека, имеющие температуру 32,5°С и 34,5°С.

Во сколько раз надо увеличить термодинамическую температуру черного тела, чтобы его энергетическая светимость возросла в 2 раза?

Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела, равна 0,6 мкм. Определить температуру тела и энергетическую светимость.

Определить спектральную плотность r_λ, энергетической светимости (излучательности), рассчитанную на 1 нм для λ в спектре излучения абсолютно черного тела. Температура тела Т = 1 К.

Вследствие изменения температуры тела максимум его спектральной энергетической светимости переместился с λ₁ = 2,5 мкм до λ₂ = 0,125 мкм. Тело абсолютно черное. Во сколько раз изменилась: а) температура тела; б) интегральная энергетическая светимость?

Металлическая поверхность площадью S = 15 см 2 , нагретая до температуры Т = 3 кК, излучает в одну минуту 100 кДж. Определить отношение энергетических светимостей этой поверхности и черного тела при данной температуре.

Металлический шар радиусом R = 1 см и теплоемкостью С = 14 Дж/К при температуре T₁ = 1200 К выброшен в межпланетное пространство. Через сколько времени температура шара уменьшится вдвое? При расчете принять, что отношение энергетических светимостей шара и АЧТ α = 0,4.

Определить энергетическую светимость тела человека при температуре t = 36 °C, принимая его за серое тело с коэффициентом поглощения k = 0,9. На какую длину волны приходится максимум излучения?

Можно условно принять, что Земля излучает как серое тело, находящееся при температуре Т = 280 К. Определить коэффициент поглощения а_T, если энергетическая светимость ее поверхности равна R_э = 325 кДж/м 2 ·ч.

Принимая коэффициент теплового излучения а_T угля при температуре Т = 600 К равным 0,8, определить: 1) энергетическую светимость угля; 2) энергию W, излучаемую с поверхности угля с площадью S = 5 см 2 за время t = 10 мин.

Диаметр вольфрамовой спирали в электрической лампочке равен 0,3 мм. длина спирали 5 см. При включении лампочки в сеть с напряжением 127 В протекает ток 0,3 А. Найти длину волны, на которую приходится максимум излучательной способности лампочки. Считать, что в равновесии все тепло теряется вследствие излучения. Отношение энергетических светимостей вольфрама и абсолютно черного тела принять равным 0,4. Ответ выразить в мкм.

Какую энергию излучает в течение суток каменное оштукатуренное здание с поверхностью общей площадью 1000 м 2 , если температура излучающей поверхности 0°С? Отношение энергетической светимости каменного оштукатуренного здания и абсолютно черного тела для данной температуры равно 0,8.

Диаметр вольфрамовой спирали в электрической лампочке d = 0,25 мм, длина спирали l = 2 см. При включении лампочки в сеть напряжением U = 127 В через лампочку течет ток I = 0,37 А. Найти температуру Т спирали. Считать, что при установлении равновесия все выделяющееся в нити тепло теряется в результате излучения. Отношение энергетической светимостей вольфрама и абсолютно черного тела данной температуры k = 0,3.

Звезда Вега имеет радиус 2,1·10 9 м, а максимум ее энергетической светимости приходится на длину волны 0,305 мкм. На каком расстоянии от этой звезды должна вращаться планета, чтобы падающий на нее поток излучения был таким же, как для Земли в солнечной системе (1,4 кВт/м 2 )? Во сколько раз это расстояние больше, чем расстояние от Солнца до Земли?

При нагревании тела длина волны, на которую приходится максимум излучательной способности, изменилась от 1,2 до 1,5 мкм. На сколько изменилась максимальная излучательная способность тела? На сколько изменилась энергетическая светимость тела?

Исследование спектра излучения Солнца показывает, что максимум энергетической светимости соответствует длине волны примерно 500 нм. Определите температуру излучающей поверхности Солнца.

Принимая Солнце за черное тело и учитывая, что максимум его энергетической светимости приходится на длину волны 500 нм, определить: 1) температуру поверхности солнца; 2) энергию, излучаемую солнцем за 1 с; 3) массу, теряемую солнцем за счет излучения за это время.

Отверстие в стенке мартеновской печи площадью 20 см 2 излучает так, что максимум его энергетической светимости приходится на длину волны 1,45 мкм. Какой тепловой поток создает это отверстие на расстоянии 1,5 м?

Раскаленная металлическая поверхность площадью 10 см 2 излучает в 1 мин 4 10 4 Дж. Температура поверхности 2500 К. Найдите: 1) Излучение этой поверхности, если бы она была абсолютно черной. 2) Отношение энергетической светимости этой поверхности и абсолютно черного тела при данной температуре.

Источник