Радиус Шварцшильда — Schwarzschild radius
Радиус Шварцшильда (иногда исторически называют гравитационным радиусом ) является физическим параметром , который появляется в решении Шварцшильда для уравнений Эйнштейна , соответствующей радиусу , определяющего горизонт событий шварцшильдовской черной дыры . Это характерный радиус, связанный с любым количеством массы. Радиус Шварцшильда был назван в честь немецкого астронома Карла Шварцшильда , который рассчитал это точное решение для общей теории относительности в 1916 году.
Радиус Шварцшильда задается как
р s знак равно 2 грамм M c 2 , <\ displaystyle r_ = <\ frac <2GM>
СОДЕРЖАНИЕ
История
В 1916 году Карл Шварцшильд получил точное решение уравнений поля Эйнштейна для гравитационного поля вне невращающегося сферически-симметричного тела с массой (см. Метрику Шварцшильда ). Решение содержало члены вида и , которые становятся сингулярными при и соответственно. Это стало известно как радиус Шварцшильда . Физическое значение этих особенностей обсуждалось десятилетиями. Было обнаружено, что точка в точке является координатной сингулярностью, что означает, что она является артефактом конкретной системы координат, которая использовалась; в то время как тот, что находится в физическом состоянии, и не может быть удален. Радиус Шварцшильда, тем не менее, является физически значимой величиной, как отмечалось выше и ниже. M <\ displaystyle M> 1 — р s / р <\ displaystyle 1- 1 1 — р s / р <\ displaystyle <\ frac <1><1- р знак равно 0 <\ displaystyle r = 0> р знак равно р s <\ displaystyle r = r_ > р s <\ displaystyle r_ > р знак равно р s <\ displaystyle r = r_ > р знак равно 0 <\ displaystyle r = 0>
Это выражение ранее вычислялось с использованием механики Ньютона как радиус сферически симметричного тела, при котором убегающая скорость равнялась скорости света. Он был обнаружен в 18 веке Джоном Мичеллом и Пьером-Симоном Лапласом .
Параметры
Радиус Шварцшильда объекта пропорционален массе. Соответственно, у Солнца есть радиус Шварцшильда приблизительно 3,0 км (1,9 мили), тогда как у Земли всего около 9 мм (0,35 дюйма ), а у Луны — около 0,1 мм (0,0039 дюйма). Масса наблюдаемой Вселенной имеет радиус Шварцшильда приблизительно 13,7 миллиарда световых лет.
| Объект | Масса, M <\ textstyle M> | Радиус Шварцшильда, 2 грамм M c 2 <\ textstyle <\ frac <2GM> | Фактический радиус, р <\ textstyle r> | Плотность Шварцшильда, или 3 c 6 32 π грамм 3 M 2 <\ textstyle <\ frac <3c ^ <6>> <32 \ pi G ^ <3>M ^ <2>>>> 3 c 2 8 π грамм р 2 <\ textstyle <\ frac <3c ^ <2>> <8 \ pi Gr ^ <2>>>> |
|---|---|---|---|---|
| Наблюдаемая Вселенная | 8,8 × 10 52 кг | 1,3 × 10 26 м (13,7 млрд св. Лет ) | 4,4 × 10 26 м (46,5 млрд св. Лет ) | 9,5 × 10 — 27 кг / м 3 |
| Млечный Путь | 1,6 × 10 42 кг | 2,4 × 10 15 м (0,25 св. Лет ) | 5 × 10 20 м (52,9 тыс. Св. Лет ) | 0,000029 кг / м 3 |
| TON 618 (самая большая из известных черных дыр ) | 1,3 × 10 41 кг | 1,9 × 10 14 м ( 1300 а.е. ) | 0,0045 кг / м 3 | |
| SMBH в NGC 4889 | 4,2 × 10 40 кг | 6,2 × 10 13 м | 0,042 кг / м 3 | |
| SMBH в Мессье 87 | 1,3 × 10 40 кг | 1,9 × 10 13 м | 0,44 кг / м 3 | |
| СМЧД в галактике Андромеды | 3,4 × 10 38 кг | 5,0 × 10 11 м | 640 кг / м 3 | |
| Стрелец А * (SMBH в Млечном Пути) | 8,2 × 10 36 кг | 1,2 × 10 10 м | 1,1 × 10 6 кг / м 3 | |
| солнце | 1,99 × 10 30 кг | 2,95 × 10 3 м | 7,0 × 10 8 м | 1,84 × 10 19 кг / м 3 |
| Юпитер | 1,90 × 10 27 кг | 2,82 м | 7,0 × 10 7 м | 2,02 × 10 25 кг / м 3 |
| земля | 5,97 × 10 24 кг | 8,87 × 10 — 3 м | 6.37 × 10 6 м | 2,04 × 10 30 кг / м 3 |
| Луна | 7,35 × 10 22 кг | 1,09 × 10 — 4 м | 1,74 × 10 6 м | 1,35 × 10 34 кг / м 3 |
| Сатурн | 5,683 × 10 26 кг | 8,42 × 10 — 1 м | 6,03 × 10 7 м | 2,27 × 10 26 кг / м 3 |
| Уран | 8,681 × 10 25 кг | 1,29 × 10 — 1 м | 2,56 × 10 7 м | 9,68 × 10 27 кг / м 3 |
| Нептун | 1.024 × 10 26 кг | 1,52 × 10 — 1 м | 2,47 × 10 7 м | 6,97 × 10 27 кг / м 3 |
| Меркурий | 3,285 × 10 23 кг | 4,87 × 10 — 4 м | 2,44 × 10 6 м | 6,79 × 10 32 кг / м 3 |
| Венера | 4,867 × 10 24 кг | 7,21 × 10 — 3 м | 6,05 × 10 6 м | 3,10 × 10 30 кг / м 3 |
| Марс | 6,39 × 10 23 кг | 9,47 × 10 — 4 м | 3,39 × 10 6 м | 1,80 × 10 32 кг / м 3 |
| Человек | 70 кг | 1,04 × 10 — 25 м | 1,49 × 10 76 кг / м 3 | |
| Планковская масса | 2,18 × 10 — 8 кг | 3,23 × 10 — 35 м | (вдвое больше планковской длины ) | 1,54 × 10 95 кг / м 3 |
Вывод
Классификация черных дыр по радиусу Шварцшильда
| Класс | Прибл. масса | Прибл. радиус |
|---|---|---|
| Сверхмассивная черная дыра | 10 5 –10 10 м вс | 0,001–400 а.е. |
| Черная дыра средней массы | 10 3 Пн вс | 10 3 км ≈ R Земля |
| Звездная черная дыра | 10 Пн вс | 30 км |
| Микро черная дыра | до M Moon | до 0,1 мм |
Любой объект, радиус которого меньше его радиуса Шварцшильда, называется черной дырой . Поверхность в радиусе Шварцшильда действует как горизонт событий в невращающемся теле ( вращающаяся черная дыра действует несколько иначе). Ни свет, ни частицы не могут выйти через эту поверхность из области внутри, отсюда и название «черная дыра».
Черные дыры можно классифицировать на основе их радиуса Шварцшильда или, что эквивалентно, по их плотности, где плотность определяется как масса черной дыры, деленная на объем ее сферы Шварцшильда. Поскольку радиус Шварцшильда линейно связан с массой, а замкнутый объем соответствует третьей степени радиуса, поэтому маленькие черные дыры намного плотнее больших. Объем, заключенный в горизонте событий наиболее массивных черных дыр, имеет среднюю плотность ниже, чем у звезд главной последовательности.
Сверхмассивная черная дыра
Сверхмассивная черная дыра (SMBH) является крупнейшим типа черной дыры, хотя есть несколько официальных критериев относительно того, как такой объект считается так, порядка сотен тысяч до миллиардов солнечных масс. ( Были обнаружены сверхмассивные черные дыры размером до 21 миллиарда (2,1 × 10 10 ) M ☉ , такие как NGC 4889 ). В отличие от черных дыр звездной массы , сверхмассивные черные дыры имеют сравнительно низкую среднюю плотность. (Обратите внимание, что (невращающаяся) черная дыра — это сферическая область в пространстве, которая окружает сингулярность в ее центре; это не сама сингулярность.) С учетом этого средняя плотность сверхмассивной черной дыры может быть меньше, чем плотность воды.
Радиус Шварцшильда тела пропорционален его массе и, следовательно, его объему, если предположить, что тело имеет постоянную плотность массы. Напротив, физический радиус тела пропорционален кубическому корню из его объема. Следовательно, поскольку тело накапливает материю с заданной фиксированной плотностью (в данном примере 997 кг / м 3 , плотность воды), его радиус Шварцшильда будет увеличиваться быстрее, чем его физический радиус. Когда тело такой плотности вырастет до примерно 136 миллионов солнечных масс (1,36 × 10 8 ) M ☉ , его физический радиус превзойдет его радиус Шварцшильда, и, таким образом, оно образует сверхмассивную черную дыру.
Считается, что подобные сверхмассивные черные дыры не образуются сразу в результате сингулярного коллапса звездного скопления. Вместо этого они могут начать жизнь в виде меньших черных дыр звездных размеров и расти за счет аккреции материи или даже других черных дыр.
Радиус Шварцшильда сверхмассивной черной дыры в Центре Галактики составляет примерно 12 миллионов километров.
Звездная черная дыра
Звездные черные дыры имеют гораздо большую среднюю плотность, чем сверхмассивные черные дыры. Если накапливать вещество с ядерной плотностью (плотность ядра атома около 10 18 кг / м 3 ; нейтронные звезды также достигают этой плотности), такое накопление будет находиться в пределах его собственного радиуса Шварцшильда около 3 M ☉ и, следовательно, будет звездной черной дырой .
Изначальная черная дыра
Небольшая масса имеет чрезвычайно малый радиус Шварцшильда. Масса, подобная Эвересту, имеет радиус Шварцшильда намного меньше нанометра . Его средняя плотность при таком размере будет настолько высока, что ни один известный механизм не сможет формировать такие чрезвычайно компактные объекты. Такие черные дыры могли образоваться на ранней стадии эволюции Вселенной, сразу после Большого взрыва , когда плотности были чрезвычайно высоки. Поэтому эти гипотетические миниатюрные черные дыры называют первичными черными дырами .
Другое использование
В гравитационном замедлении времени
Гравитационное замедление времени вблизи большого, медленно вращающегося, почти сферического тела, такого как Земля или Солнце, может быть разумно следующим:
т р т знак равно 1 — р s р <\ displaystyle <\ frac
t r — время, прошедшее для наблюдателя при радиальной координате r в гравитационном поле; t — время, прошедшее для наблюдателя, удаленного от массивного объекта (и, следовательно, вне гравитационного поля); r — радиальная координата наблюдателя (аналогична классическому расстоянию от центра объекта); r s — радиус Шварцшильда.
Радиус Шварцшильда для массы Планка
Для массы Планка радиус Шварцшильда и длина волны Комптона того же порядка, что и длина Планка . м п знак равно ℏ c / грамм <\ Displaystyle м _ <\ rm
> = <\ sqrt <\ hbar c / G>>> р S знак равно 2 ℓ п <\ Displaystyle г _ <\ rm > = 2 \ ell _ <\ rm
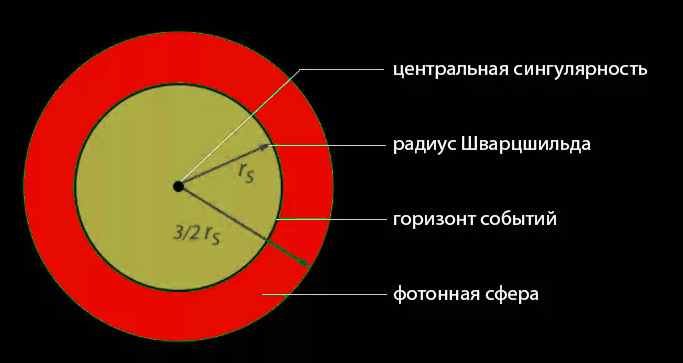
>> >> > = <\ sqrt <\ hbar G / c ^ <3>>>> Классификация черных дыр по типу: Классификация черных дыр по массе: Источник Радиус Шварцшильда и Сингулярность — Горизонт событий черной дыры — Как проходит процесс появления черной дыры? Известно, что черные дыры образуются тогда, когда на материю воздействует запредельная по силе гравитация, что может случится, например, при “схлопывании” (коллапсе) звезды, массой в пару десятков раз превышающей Солнце. Где находится тот самый предел, до которого сжатая материя все ещё остается вполне ощутимым физическим объектом, а после которого – “проваливается сама в себя”, образуя черную дыру? Такой предел существует и в самом деле – черная дыра образуется, только тогда, когда определенное количество вещества сжато в сферу, с радиусом, равным радиусу Шварцшильда. Сам же радиус Шварцшильда представляет собой величину, которую можно определить для любого тела обладающего массой, и на которой находился бы горизонт событий, создаваемый этой массой (проще говоря – размер шарика до которого можно “уплотнить” материю без превращения в черную дыру). Термин был введен в обиход немцем Карлом Шварцшильдом в 1916 году. Наглядная схема того «как устроена» черная дыра Как происходит превращение звезды в черную дыру? Если в начале коллапса масса звезды (ее ядра или всего того, что от нее осталось) превышает 3 массы Солнца, то сжатие будет продолжаться до тех пор, пока все вещество звезды не окажется сосредоточенным в некоторой точке, называемой сингулярностью. В сингулярности вещество сжато до бесконечной плотности бесконечно большими гравитационными силами, иначе говоря, кривизна пространства-времени в сингулярности бесконечна. Однако современная физика пока еще не в состоянии оперировать бесконечными силами и плотностями; поэтому можно считать, что законы природы — в том смысле, как мы их понимаем — в сингулярности утрачивают силу. Если говорить совсем по простому, вещество из которого состояла сколлапсировавшая звезда в сингулярности перестает существовать. Как только сколлапсировавшая звезда сжимается в сферу шварцшильдовского радиуса, она исчезает для наблюдателя, поскольку свет ее поверхности уже не может достичь нас. В этом случае мы говорим о формировании некоего горизонта, и все происходящее в пределах этого горизонта недоступно нашему наблюдению. Есть основания полагать, что там звезда продолжает коллапсировать в сингулярность, но мы в принципе не имеем возможности наблюдать этот процесс или каким-либо другим путем получать информацию о превращениях звездного вещества. Черная дыра, образовавшаяся в результате коллапса массивной звезды,— это сферический объем пространства, имеющий радиус, равный радиусу Шварцшильда, и сингулярность—в центре. Граница черной дыры носит название горизонта событий, так как никакие сведения о событиях внутри черной дыры не могут распространяться во Вселенной за пределами этого горизонта. У черной дыры, разумеется, нет твердой поверхности. Если бы вам пришлось пересекать горизонт событий, то вы не заметили бы никаких изменений пространства, но, оказавшись внутри этой границы, вы уже не смогли бы двигаться назад и с неизбежностью упали бы на центральную сингулярность. Горизонт событий — это односторонняя граница. Все вещественные объекты, свет и любое другое излучение могут падать в черную дыру, но ничто не может покинуть ее. Если не в действительности, то по крайней мере в принципе почти любого количества вещества достаточно для формирования черной дыры. Каждой величине массы соответствует свое значение радиуса Шварцшильда, внутри которого эта масса должна быть заключена. Чтобы составить некоторое представление о величине радиуса Шварцшильда, укажем, что для Солнца он должен быть немного меньше 3 км. То есть если вся масса Солнца окажется внутри сферы такого радиуса, то Солнце превратится в черную дыру. Нетрудно подсчитать, что при нынешнем радиусе Солнца (700 000 км) плотность его вещества, сжатого в сферу шварцшильдского радиуса, в 10 раз превысит плотность воды. Если бы какой-нибудь физик вдруг задумал сделать черную дыру из нашей планеты, то ему пришлось бы сжать Землю в сферу радиусом меньше 30 см! Впрочем, это чисто теоретический подсчет. В реальности все несколько сложнее. При нынешнем состоянии Вселенной ни Солнце, ни Земля не могут сами по себе превратиться в черные дыры. Массы не хватит! Звезды, имеющие к концу своей жизни массу меньше 2—3 солнечных, в основном становятся не черными дырами, а белыми карликами или нейтронными звездами. Однако известно много звезд, масса которых значительно превышает этот предел, и, хотя к концу своей эволюции звезды многими способами могут избавиться от излишков вещества, весьма вероятно, что некоторые из таких сверхмассивных звезд на последнем этапе своего существования все-таки становятся черными дырами. Шварцшильдовский радиус звезды массой 10 солнечных составляет примерно 30 км. Так как объем сферы пропорционален кубу радиуса, а радиус черной дыры зависит от ее массы, выходит, что плотность вещества, сжатого до размеров сферы Шварцшильда, имеет меньшее значение для звезд большей массы. Так, звезда массой 10 солнечных в тот момент, когда в процессе коллапса ее радиус окажется равным радиусу Шварцшильда, будет иметь плотность всего лишь в 10 4 раз выше плотности воды, а средняя плотность вещества нейтронных звезд составляет, по нашим представлениям, 10 8 кг/м3. Поскольку у нас нет сомнений в факте существования нейтронных звезд, то, очевидно, вещество может быть сжато до таких огромных значений плотности, а, как мы только что выяснили, плотность коллапсирующей массивной звезды в тот момент, когда она становится черной дырой, на порядок меньше плотности нейтронной звезды. Конечно, внутри черной дыры коллапс будет продолжаться до тех пор, пока плотность вещества не станет бесконечной, но, что бы ни происходило внутри, факт остается фактом: черные дыры могут образовываться из вещества с плотностью, заведомо меньшей плотности объектов, существование которых во Вселенной твердо установлено. Развивая эту мысль дальше, находим, например, что черная дыра массой 10 солнечных будет иметь радиус около 300 млн. км (т. е. вдвое больше радиуса земной орбиты), а средняя плотность вещества при “уходе” его за горизонт событий окажется почти равной плотности воды. Черная дыра массой в несколько миллиардов масс Солнца в момент своего формирования будет иметь такую же плотность, как воздух у поверхности Земли. Стоит еще раз подчеркнуть, что если вещество объекта данной массы сжалось до сферы радиуса Шварцшильда, то уже ничто не в состоянии воспрепятствовать его бесконечному коллапсу, однако для формирования черной дыры никакого невероятного сжатия материи не требуется. Источникλ C знак равно 2 π ℓ п <\ displaystyle \ lambda _ <\ rm ℓ п знак равно ℏ грамм / c 3 <\ displaystyle \ ell _ <\ rm Смотрите также
Шварцшильдовская черная дыра
Радиус Шварцшильда и Сингулярность
Горизонт событий черной дыры
Как проходит процесс появления черной дыры?
