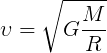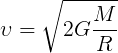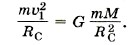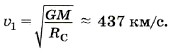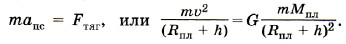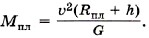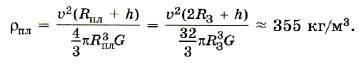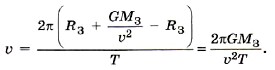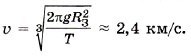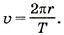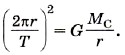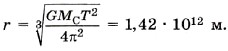Формулы и калькулятор космических скоростей
Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса. Для быстрого расчета можно воспользоваться онлайн-калькулятором.
Первая космическая скорость
Первая космическая скорость — это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты, чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет не круговой, а эллипсоидной.
Формула первой космической скорости:
где G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10 -11 м 3 /(кг*с 2 ), или Н*м 2 /кг 2
R — радиус небесного тела
M — масса небесного тела
Вторая космическая скорость
Вторая космическая скорость — это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.
Формула второй космической скорости:
где G — гравитационная постоянная
R — радиус небесного тела
M — масса небесного тела
Пример:
Масса планеты Земля составляет 5,9726*10 24 кг, средний радиус — 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.
Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна — 1,0243*10 26 кг. средний радиус — 24 622 км (24 622 000 м). В итоге получим значения — 16 663 м/с и 23 565 м/с.
Значения для Марса (6,4171*10 23 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с. Для Венеры (4,8675*10 24 кг и 6051,8 км) — 7 327 м/с и 10 362 м/с соответственно.
Источник
Первая космическая скорость
Первая космическая скорость – это скорость, с которой спутник движется вокруг планеты по круговой орбите, не удаляясь от планеты и не падая на нее.
То есть, для первой космической скорости орбита — это окружность. Расстояние от центра планеты до спутника равно \( R = \left( r + h \right) \). Это представлено на рисунке 1.
Формула для вычисления первой космической скорости
Первую космическую скорость можно посчитать по формуле:
\( v \left( \frac<\text<м>><\text
\( M \left( \text <кг>\right) \) (килограммы) — масса планеты, вокруг которой движется спутник
\( r \left( \text <м>\right) \) (метры) – радиус планеты
\( h \left( \text <м>\right) \) (метры) — расстояние от поверхности планеты до спутника
\(G \ = 6<,>67 \cdot 10^ <-11>\left( \text <Н>\cdot \frac<\text<м>^2><\text<кг>^2> \right)\) — гравитационная постоянная
Первая космическая скорость в цифрах для некоторых небесных тел
первая космическая скорость у поверхности Земли \( v = 8000 \left( \frac<\text<м>><\text
первая космическая скорость у поверхности Солнца \( v = 437000 \left( \frac<\text<м>><\text
первая космическая скорость у поверхности Луны \( v = 1680 \left( \frac<\text<м>><\text
первая космическая скорость у поверхности Марса \( v = 3530 \left( \frac<\text<м>><\text
Как выводится формула первой космической скорости
Рассмотрим движение спутника вокруг Земли.
Земля и спутник притягиваются, запишем закон притяжения между планетой и спутником
При круговом движении на спутник действует центростремительная сила (как и на любое тело при таком движении).
Мы можем записать эти уравнения в виде системы.
\[ \begin
Земля и спутник притягиваются, благодаря этому спутник движется вокруг Земли по круговой орбите. Значит, притяжение между спутником и Землей – это центростремительная сила. Именно она заставляет спутник двигаться вокруг планеты по окружности. На языке математики это запишется так:
А если равны левые части уравнений, то будут равны и правые:
Масса \( m \) спутника и расстояние \( R \) между телами встречается в обеих частях уравнения. Поделим обе части уравнения на массу спутника.
Теперь умножим обе части уравнения на расстояние \(\left( r + h \right) \). Получим:
Извлечем корень квадратный из обеих частей уравнения, чтобы получить скорость:
Вам будет интересно почитать:
Движение по окружности, центростремительная сила и центростремительное ускорение
Источник
Космическая скорость
Вычисляет 1-ю (орбитальную), 2-ю (скорость убегания) и 3-ю (скорость покидания системы) космические скорости для заданных параметров планеты.
С древних времен людей интересовала проблема устройства мира. Еще в III-м веке до нашей эры греческий философ Аристарх Самосский высказал идею о том, что Земля вращается вокруг Солнца, и попытался вычислить расстояния и размеры Солнца и Земли по положению Луны. Так как доказательный аппарат Аристарха Самосского был несовершенен, большинство осталось сторонниками пифагорейской геоцентрической системы мира.
Прошло почти два тысячелетия, и идеей гелиоцентрического устройства мира увлекся польский астроном Николай Коперник. Он умер в 1543 году, и вскоре труд всей его жизни опубликовали ученики. Модель и таблицы положения небесных тел Коперника, основанные на гелиоцентрической системе, гораздо точнее отражали положение вещей.
Спустя полвека немецкий математик Иоганн Кеплер, используя скурупулезные записи датского астронома Тихо Браге о наблюдениях небесных тел, вывел законы движения планет, которые сняли неточности модели Коперника.
Завершение XVII века ознаменовалось трудами великого английского ученого Исаака Ньютона. Законы механики и всемирного тяготения Ньютона расширили и дали теоретическое обоснование формулам, выведенным из наблюдений Кеплером.
Наконец, в 1921 году Альберт Эйнштейн предложил общую теорию относительности, наиболее точно описывающую механику небесных тел в настоящее время. Ньютоновские формулы классической механики и теории гравитации до сих пор могут применяться для некоторых вычислений, не требующих большой точности, и там, где релятивистскими эффектами можно пренебречь.
Благодаря Ньютону и его предшественникам мы можем вычислить:
- какую скорость должно иметь тело для сохранения заданной орбиты (первая космическая скорость)
- с какой скоростью должно двигаться тело, чтобы оно преодолело притяжение планеты и стало спутником звезды (вторая космическая скорость)
- минимальную необходимую скорость выхода за пределы планетной системы (третья космическая скорость)
Источник
§ 32. Примеры решения задач по теме «Первая космическая скорость
Для решения задач требуется знать закон всемирного тяготения, закон Ньютона, а также связь линейной скорости тел с периодом их обращения вокруг планет. Обратите внимание на то, что радиус траектории спутника всегда отсчитывается от центра планеты.
Задача 1. Вычислите первую космическую скорость для Солнца. Масса Солнца 2 • 10 30 кг, диаметр Солнца 1,4 • 10 9 м.
Р е ш е н и е. Спутник движется вокруг Солнца под действием единственной силы — силы тяготения. Согласно второму закону Ньютона запишем:
Из этого уравнения определим первую космическую скорость, т. е. минимальную скорость, с которой надо запустить тело с поверхности Солнца, чтобы оно стало его спутником:
Задача 2. Вокруг планеты на расстоянии 200 км от её поверхности со скоростью 4 км/с движется спутник. Определите плотность планеты, если её радиус равен двум радиусам Земли (Rпл = 2R3).
Р е ш е н и е. Планеты имеют форму шара, объём которого можно вычислить по формуле 
где Мпл — масса планеты, Rпл — её радиус.
Спутник движется вокруг планеты по круговой орбите. На него действует сила тяготения Fтяг, которая определяет центростремительное ускорение.
Согласно второму закону Ньютона
Из последнего уравнения находим массу планеты:
Подставив это выражение в формулу (1), имеем
Задача 3. При какой скорости спутника период его обращения вокруг Земли равен двум суткам?
Р е ш е н и е. Скорость спутника
где h — высота спутника над поверхностью Земли.
Для определения скорости необходимо знать высоту h.
Спутник движется по круговой орбите, при этом сила тяготения является центростремительной силой. Согласно второму закону Ньютона для спутника запишем:
где m — масса спутника.
Из уравнения (2) находим высоту 
Для упрощения расчётов поместим спутник на полюс, где сила тяжести равна силе тяготения. Тогда 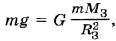
Подставив найденное выражение в формулу (3), определим скорость:
Задача 4. Определите среднее расстояние от Сатурна до Солнца, если период обращения Сатурна вокруг Солнца равен 29,5 лет. Масса Солнца равна 2 • 10 30 кг.
Р е ш е н и е. Считаем, что Сатурн движется вокруг Солнца по круговой орбите. Тогда согласно второму закону Ньютона запишем:
где m — масса Сатурна, r — расстояние от Сатурна до Солнца, Мс — масса Солнца.
Период обращения Сатурна 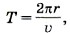
Подставив выражение для скорости υ в уравнение (4), получим
Из последнего уравнения определим искомое расстояние от Сатурна до Солнца:
Сравнив с табличными данными, убедимся в правильности найденного значения.
Задачи для самостоятельного решения
1. Определите длительность года на Венере. Среднее расстояние от Венеры до Солнца 1,08 • 10 8 км, а от Земли до Солнца 1,49 • 10 8 км.
2. Какой импульс силы подействовал на спутник массой 1 т, если спутник перешёл с орбиты радиусом R3 + h на орбиту радиусом R3 + 2h, где высота h равна 200 км?
3. Астероид вращается вокруг Солнца с периодом, равным 410 сут. Определите расстояние от астероида до Солнца.
Образцы заданий ЕГЭ
С1. Чему равен радиус кольца Сатурна, в котором частицы движутся со скоростью 10 км/с? Масса Сатурна 5,7 • 10 26 кг.
С2. Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн км, а от планеты Юпитер до Солнца — 778,3 млн км. Чему равно отношение υЗ/υЮ линейных скоростей этих двух планет при их движении вокруг Солнца, если считать их орбиты окружностями?
С3. Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн км, а до планеты Земля — 149,6 млн км. Чему приблизительно равна средняя линейная скорость планеты Уран при её движении вокруг Солнца, если известно, что средняя скорость движения Земли по орбите вокруг Солнца составляет 30 км/с?
С4. Средняя плотность некоторой планеты равна средней плотности планеты Земля, а радиус этой планеты в 2 раза больше радиуса Земли. Определите отношение первой космической скорости на этой планете к первой космической скорости на Земле υп/υ3.
Источник