Резонанс луны с землей
Если свести в таблицу орбитальные периоды и периоды вращения всех тел Солнечной системы, то обнаружится соизмеримость многих периодов. Это указывает на существование ряда резонансных явлений между взаимосвязанными резонаторами. Имеются резонансы между орбитальными периодами членов одноа и той же системы, а также резонансы между орбитальными периодами и осевыми периодами вращающихся тел.
По-видимому, резонансы являются крайне важными особенностями Солнечной системы. Тела, однажды попавшие в резонанс, могут при определенных условиях оставаться захваченными резонансом неограниченно долго; следовательно, резонансная структура стабилизирует Солнечную систему на очень большие периоды времени.
Изучение резонансной структуры в пределах какой-либо системы может дать полезную информацию об эволюции этой системы. Чтобы сделать какие-нибудь выводы относительно эволюции системы, мы должны выяснить, как установилась данная резонансная структура. Предлагалось два различных механизма.
1. В соответствии с первым механизмом, предложенным Голдрайхом [189], первоначально тела возникли без резонансов между их периодами вращения и орбитальными периодами (исключая те, которые обязательно возникают при случайном распределении). Более поздняя эволюция системы, в основном в результате приливных явлений, изменила их периоды различным образом и привела к установлению резонансов.
Эта теория ни в коей мере не может дать общее объяснение резонансам. Она применима только к системам спутников, а поскольку приливные воздействия планет на Солнце в общем пренебрежимо малы, для объяснения возникновения резонансов в планетной системе необходимо привлечь другой процесс. Далее, объяснение резонансов приливными воздействиями приводит
к трудностям даже в случае резонансов спутников. Например, поскольку (см. разд. 18.6) происхождение щели Кассини генетически связано с Мимасом, орбита Мимаса с гетегонного времени не могла измениться более чем на 1—2%. Следовательно, здесь нет места для значительной приливной эволюции.
2. В соответствии с альтернативным предположением [21] резонансные явления сами по себе были существенны в гетегонных процессах, так что тела возникали преимущественно в состоянии резонанса с другими телами. Следовательно, резонансная структура может дать нам прямую информацию о гетегонных процессах.
8.1.1. РАЗЛИЧНЫЕ ВИДЫ РЕЗОНАНСА
В Солнечной системе наблюдаются следующие виды резонансов (табл. 8.1.1).
Таблица 8.1.1 (см. скан) Виды резонансов
1. Резонансы, между орбитальными движениями. Если для периодов орбит 
где 
Исследовались также [356] резонансы между орбитальными движениями планеты и одного из ее спутников. При наблюдении в системе координат, связанной с планетой, такой резонанс проявляется как резонанс между видимым движением спутника и видимым движением Солнца. Его иногда называют «спутниково-солнечным резонансом».
2. Резонансы между вращением и орбитальным движением. Если плотность во вращающемся теле распределена асимметрично, то 
Подобная асимметрия планеты может также влиять на движение спутника, обращающегося относительно планеты. Неизвестно, насколько существенно это взаимодействие в настоящее время, но оно могло влиять на эволюцию системы Земля — Луна (см. гл. 24).
Если спутник вызывает приливы на центральном теле, приливные горбы вовлекаются в совместное вращение со спутником. Взаимодействие между приливными горбами и спутником можно рассматривать как резонанс между вращением и орбитальным движением с
Источник
Орбитальный резонанс
Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти тела периодически сближаются, находясь в определённых точках своих орбит. Возникающие вследствие этого регулярные изменения силы гравитационного взаимодействия этих тел могут стабилизировать их орбиты.
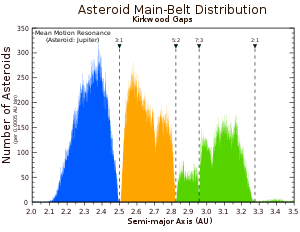
В некоторых случаях резонансные явления вызывают неустойчивость некоторых орбит. Так, щели Кирквуда в поясе астероидов объясняются резонансами с Юпитером; деление Кассини в кольцах Сатурна объясняются резонансом со спутником Сатурна Мимасом.
Содержание
Примеры
- Плутон и некоторые другие объекты пояса Койпера (так называемые плутино) находятся в орбитальном резонансе 2:3 с Нептуном — два оборота Плутона вокруг Солнца соответствуют по времени трём оборотам Нептуна.
- Сатурн и Юпитер находятся почти в точном резонансе 2:5;
- Троянские астероиды находятся в резонансе 1:1 с Юпитером;
- Спутники Юпитера Ганимед, Европа и Ио находятся в резонансе 1:2:4;
- Спутники Плутона находятся в резонансе 2:3:12;
- Комета Энке находится в орбитальном резонансе 5:1 с Юпитером.
Спин-орбитальный резонанс
Близким явлением является спин-орбитальный резонанс, когда синхронизируется орбитальное движение небесного тела и его вращение вокруг своей оси:
- Меркурий обращается вокруг Солнца в спин-орбитальном резонансе 3:2, то есть за два меркурианских года планета совершает три оборота вокруг своей оси.
- Луна при вращении вокруг Земли обращена всегда одной стороной — спин-орбитальный резонанс 1:1.
- Все Галилеевы спутники также обращены к Юпитеру одной стороной.
См. также
Ссылки
- Впервые найден орбитальный резонанс трёх планет
- Locations of Solar System Planetary Mean-Motion Resonances. Web calculator that plots distributions of the semimajor axes (or in one case the perihelion distances) of the minor planets in relation to mean motion resonances of the planets (website maintained by M.A. Murison). (англ.)
 Небесная механика Небесная механика | |
|---|---|
| Законы и задачи | Законы Ньютона • Закон всемирного тяготения • Законы Кеплера • Задача двух тел • Задача трёх тел • Гравитационная задача N тел • Задача Бертрана • Уравнение Кеплера |
| Небесная сфера | Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая • Международная небесная система координат • Сферическая система координат • Ось мира • Небесный экватор • Прямое восхождение • Склонение • Эклиптика • Равноденствие • Солнцестояние • Фундаментальная плоскость |
| Параметры орбит | Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра • Апоцентр и перицентр • Орбитальная скорость • Узел орбиты • Эпоха |
| Движение небесных тел | Движение Солнца и планет по небесной сфере • Эфемериды Конфигурации планет: противостояние • квадратура • парад планет • Кульминация • Сидерический период • Орбитальный резонанс • Период вращения • Предварение равноденствий • Синодический период • Сближение Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл • Покрытие • Прохождение • Либрация • Элонгация • Эффект Козаи • Эффект Ярковского • Эффект Джанибекова |
| Астродинамика | |
| Космический полёт | Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая Формула Циолковского • Гравитационный манёвр • Гомановская траектория • Метод оскулирующих элементов • Приливное ускорение • Изменение наклонения орбиты • Стыковка • Точки Лагранжа • Эффект «Пионера» |
| Орбиты КА | Геостационарная орбита • Гелиоцентрическая орбита • Геосинхронная орбита • Геоцентрическая орбита • Геопереходная орбита • Низкая опорная орбита • Полярная орбита • Тундра-орбита • Солнечно-синхронная орбита • Молния-орбита • Оскулирующая орбита |
Wikimedia Foundation . 2010 .
Смотреть что такое «Орбитальный резонанс» в других словарях:
Резонанс — Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания Резонанс (фр. resonance, от лат. r … Википедия
Формирование и эволюция Солнечной системы — Согласно современным представлениям, формирование Солнечной системы началось около 4,6 млрд лет назад с гравитационного коллапса небольшой части гигантского межзвёздного молекулярного облака. Большая часть вещества оказалась в гравитационном … Википедия
Происхождение и эволюция Миранды — Миранда в натуральном цвете Происхождение и эволюция Миранды, одного из спутников Урана, полны интересными геологическими событиями[1] … Википедия
Аурелия и Голубая луна — (англ. Aurelia and Blue Moon) гипотетические примеры планеты и луны, на которых могла бы возникнуть внеземная жизнь. Этот проект явился результатом плодотворного сотрудничества телекомпании Blue Wave Productions Ltd. и группы американских и… … Википедия
Миранда (спутник) — У этого термина существуют и другие значения, см. Миранда. Миранда … Википедия
Ганимед (спутник) — Ганимед Изоб … Википедия
Щели Кирквуда — … Википедия
Пояс астероидов — Схема расположения пояса астероидов в Солнечной системe … Википедия
(84522) 2002 TC302 — 2002 ТС302 … Википедия
Kepler-9 — Координаты: 19ч 2м 17.756с, +38° 24′ 3.18″ … Википедия
Источник
Орбитальный резонанс — Orbital resonance
В небесной механике , орбитальный резонанс возникает , когда орбитальные тела оказывают регулярное, периодическое гравитационное влияние друг на друг, как правило , из — за их орбитальные периоды связаны соотношением малых целых чисел . Чаще всего эта связь обнаруживается между парой объектов. Физический принцип, лежащий в основе орбитального резонанса, аналогичен понятию толкания ребенка на качелях , при этом и орбита, и качели имеют собственную частоту , а тело, выполняющее «толкание», будет действовать периодически, чтобы иметь кумулятивный эффект на качели. движение. Орбитальные резонансы значительно усиливают взаимное гравитационное влияние тел (т. Е. Их способность изменять или ограничивать орбиты друг друга). В большинстве случаев это приводит к нестабильному взаимодействию, при котором тела обмениваются импульсом и перемещаются по орбитам до тех пор, пока резонанс не перестанет существовать. При некоторых обстоятельствах резонансная система может быть самокорректирующейся и, следовательно, стабильной. Примерами являются 1: 2: 4 резонанс Jupiter спутников «S Ганимед , Европа и Ио , и 2: 3 резонанса между Плутоном и Нептуном . Неустойчивые резонансы с внутренними лунами Сатурна вызывают разрывы в кольцах Сатурна . Частный случай резонанса 1: 1 между телами с одинаковыми радиусами орбиты заставляет большие тела солнечной системы выбрасывать большинство других тел, разделяющих их орбиты; это часть гораздо более обширного процесса очистки окрестностей , эффекта, который используется в текущем определении планеты .
Соотношение бинарного резонанса в этой статье следует интерпретировать как отношение количества орбит, совершенных за один и тот же интервал времени, а не как отношение орбитальных периодов , которое было бы обратным соотношением. Таким образом, соотношение 2: 3, приведенное выше, означает, что Плутон совершает два оборота за время, необходимое Нептуну, чтобы пройти три. В случае резонансных соотношений между тремя или более телами может использоваться любой тип отношения (при этом последовательности наименьших целочисленных соотношений не обязательно являются инверсиями друг друга), и тип отношения будет указан.
СОДЕРЖАНИЕ
История
С момента открытия закона всемирного тяготения Ньютона в 17 веке стабильность Солнечной системы волновала многих математиков, начиная с Пьера-Симона Лапласа . Устойчивые орбиты, возникающие в приближении двух тел, игнорируют влияние других тел. Влияние этих дополнительных взаимодействий на стабильность Солнечной системы очень невелико, но сначала не было известно, могут ли они складываться в течение более длительных периодов времени, чтобы значительно изменить параметры орбиты и привести к совершенно другой конфигурации, или же какие-то другие стабилизирующие эффекты могут поддерживать конфигурацию орбит планет.
Именно Лаплас нашел первые ответы, объясняющие связанные орбиты галилеевых спутников (см. Ниже). До Ньютона также учитывались соотношения и пропорции в орбитальных движениях, в том, что называлось «музыкой сфер» или musica universalis .
Статья о резонансных взаимодействиях описывает резонанс в общей современной обстановке. Первичный результат исследования динамических систем — открытие и описание очень упрощенной модели синхронизации мод; это осциллятор, который периодически получает толчки из-за слабой связи с каким-либо приводным двигателем. Аналогом здесь может быть то, что более массивное тело обеспечивает периодический гравитационный толчок меньшему телу, когда оно проходит мимо. Области синхронизации мод получили название языков Арнольда .
Типы резонанса
В общем, орбитальный резонанс может
- включают один или любую комбинацию параметров орбиты (например, эксцентриситет по отношению к большой полуоси или эксцентриситет по отношению к наклону ).
- действовать в любом временном масштабе от краткосрочного, соизмеримого с периодами обращения, до векового , измеряемого от 10 4 до 10 6 лет.
- привести либо к длительной стабилизации орбит, либо стать причиной их дестабилизации.
Среднего-орбитальное движение резонанс возникает , когда два тела имеет периоды вращения , которые являются простым числом отношением друг к другу. В зависимости от деталей это может либо стабилизировать, либо дестабилизировать орбиту. Стабилизация может произойти, когда два тела движутся так синхронно, что никогда не сближаются. Например:
- Орбиты Плутона и плутино стабильны, несмотря на то , что они пересекают орбиты гораздо большего Нептуна , потому что они находятся в резонансе 2: 3 с ним. Резонанс гарантирует, что, когда они приближаются к перигелию и орбите Нептуна, Нептун постоянно находится далеко (в среднем четверть своей орбиты). Другие (гораздо более многочисленные) пересекающие Нептун тела, которые не находились в резонансе, были выброшены из этой области сильными возмущениями, вызванными Нептуном. Существуют также меньшие, но значительные группы резонансных транснептуновых объектов, занимающих , среди прочего, резонансы 1: 1 ( трояны Нептуна ), 3: 5 , 4: 7 , 1: 2 ( два ) и 2: 5 относительно Нептуна. .
- В поясе астероидов за 3,5 а.е. от Солнца резонансы 3: 2, 4: 3 и 1: 1 с Юпитером населены скоплениями астероидов (семейство Хильда , несколько астероидов Туле и многочисленные троянские астероиды соответственно) .
Орбитальные резонансы также могут дестабилизировать одну из орбит. Этот процесс можно использовать для поиска энергоэффективных способов спуска космических аппаратов с орбиты . Для маленьких тел дестабилизация гораздо более вероятна. Например:
- В поясе астероидов в пределах 3,5 а.е. от Солнца главными резонансами среднего движения с Юпитером являются местоположения промежутков в распределении астероидов, промежутков Кирквуда (особенно в 4: 1, 3: 1, 5: 2, 7: 3 и 2: 1 резонансы). Астероиды выбрасывались с этих почти пустых переулков из-за повторяющихся возмущений. Тем не менее, в этих резонансах или вблизи них все еще есть популяции астероидов. Например, астероиды семейства Алинда находятся в резонансе 3: 1 или близки к нему, причем их орбитальный эксцентриситет постоянно увеличивается за счет взаимодействия с Юпитером, пока они в конечном итоге не столкнутся с внутренней планетой, которая выбрасывает их из резонанса.
- В кольцах Сатурна , то Отдел Кассини представляет собой зазор между внутренней B кольцом и внешним кольцом , который был очищен с помощью 2: 1 резонанс с луной Мимасом . (В частности, местом резонанса является зазор Гюйгенса , ограничивающий внешний край кольца B. )
- В кольцах Сатурна промежутки Энке и Киллера в кольце А очищаются резонансами 1: 1 со встроенными лунными лунами Паном и Дафнисом , соответственно. Внешний край кольца А поддерживается дестабилизирующим резонансом 7: 6 с луной Янусом .
Большинство тел, находящихся на резонансной орбите, движутся в одном направлении; однако ретроградный астероид 514107 Каэпаокаавела, по- видимому, находится в стабильном (в течение как минимум миллиона лет) резонансе 1: -1 с Юпитером. Кроме того, было обнаружено несколько ретроградных дамоклоидов , временно захваченных в резонансе среднего движения с Юпитером или Сатурном . Такие орбитальные взаимодействия слабее, чем соответствующие взаимодействия между телами, вращающимися в одном направлении.
Лаплас резонанса является трехчастичным резонансом с 1: 2: 4 орбитальным отношением периода (эквивалентен 4: 1 соотношение орбит: 2). Этот термин возник потому, что Пьер-Симон Лаплас обнаружил, что такой резонанс управляет движениями спутников Юпитера Ио , Европы и Ганимеда . Теперь он также часто применяется к другим резонансам трех тел с такими же соотношениями, например, между внесолнечными планетами Gliese 876 c, b и e. Трехчастичные резонансы, включающие другие простые целочисленные отношения, были названы «подобными Лапласу» или «типу Лапласа».
Линдбладовский резонанс приводы спиральных волны плотности как в галактиках (где звезды подлежат заставляя сами спиральными ветвями) и в кольцах Сатурна (где кольцо частица подлежит принуждая от спутников Сатурна ).
Светское резонанс возникает , когда прецессии двух орбит синхронизировано (обычно прецессии перигелия или восходящего узла ). Маленькое тело, находящееся в вековом резонансе с гораздо большим (например, планетой ), будет прецессировать с той же скоростью, что и большое тело. За долгое время (около миллиона лет) вековой резонанс изменит эксцентриситет и наклон маленького тела.
Несколько ярких примеров светского резонанса связаны с Сатурном. Резонанс между прецессией оси вращения Сатурна и осью орбиты Нептуна (обе имеют периоды около 1,87 миллиона лет) был идентифицирован как вероятный источник большого наклона оси Сатурна (26,7 °). Изначально Сатурн, вероятно, имел наклон ближе к Юпитеру (3,1 °). Постепенное истощение пояса Койпера уменьшило бы скорость прецессии орбиты Нептуна; в конце концов частоты совпали, и осевая прецессия Сатурна была захвачена в спин-орбитальный резонанс, что привело к увеличению угла наклона Сатурна. (Угловой момент орбиты Нептуна в 10 4 раз больше скорости вращения Сатурна и, таким образом, доминирует во взаимодействии.)
Перигелий светское резонанс между астероидами и Сатурном ( ν 6 = г — г 6 ) помогает формировать пояс астероидов (индекс «6» указует Сатурн как шестая планета от Солнца). Астероиды, которые приближаются к нему, постепенно увеличивают свою эксцентриситет, пока они не станут пересекающими Марс , после чего они обычно выбрасываются из пояса астероидов при близком прохождении к Марсу . Этот резонанс формирует внутреннюю и «боковую» границы пояса астероидов около 2 а.е. при наклонах около 20 °.
Численное моделирование показало, что возможное образование векового резонанса перигелия между Меркурием и Юпитером ( g 1 = g 5 ) может значительно увеличить эксцентриситет Меркурия и, возможно, дестабилизировать внутреннюю часть Солнечной системы через несколько миллиардов лет.
Титан Кудряшка внутри Сатурн кольца С представляет собой другой тип резонанса , в котором скорость апсидальной прецессии одной орбиты точно соответствует скорости вращения другого. Внешний конец этого эксцентричного колечка всегда указывает на Титан , главный спутник Сатурна .
Козаи резонанс возникает , когда наклон и эксцентриситет возмущенных орбит колеблются синхронно (увеличение эксцентриситета при одновременном уменьшении наклона и наоборот). Этот резонанс применим только к телам на сильно наклоненных орбитах; как следствие, такие орбиты имеют тенденцию быть нестабильными, поскольку растущий эксцентриситет приведет к появлению небольших перицентров , что обычно приводит к столкновению или (для больших лун) разрушению под действием приливных сил .
В примере другого типа резонанса, включающего эксцентриситет орбиты, эксцентриситеты Ганимеда и Каллисто изменяются с общим периодом 181 год, хотя и с противоположными фазами.
Резонансы среднего движения в Солнечной системе
В Солнечной системе есть только несколько известных резонансов среднего движения (MMR), включающих планеты, карликовые планеты или более крупные спутники (гораздо большее число включает астероиды , планетные кольца , лунные орбиты и более мелкие объекты пояса Койпера , включая множество возможных карликовых планет ).
- 2: 3 Плутон — Нептун (также Оркус и другие плютино )
- 2: 4 Тефия — Мимас (спутники Сатурна). Не упрощается, потому что необходимо учитывать либрацию узлов.
- 1: 2 Диона — Энцелад (спутники Сатурна)
- 3: 4 Гиперион — Титан (спутники Сатурна)
- 1: 2: 4 Ганимед — Европа — Ио (спутники Юпитера, соотношение орбит ).
Кроме того, считается , что Хаумеа находится в резонансе 7:12 с Нептуном, а 225088 Гонггон, как полагают, находится в резонансе 3:10 с Нептуном.
Простые целочисленные отношения между периодами скрывают более сложные отношения:
- точка соединения может колебаться ( либрировать ) вокруг точки равновесия, определяемой резонансом.
- данные ненулевые эксцентриситеты , то узлы или periapsides могут дрейфовать (родственный резонанс, короткий период, а не светская прецессии).
В качестве иллюстрации последнего рассмотрим хорошо известный резонанс Ио-Европы 2: 1. Если бы периоды обращения были в этом отношении, средние движения (обратные периодам, часто выражаемые в градусах в день) удовлетворяли бы следующему п <\ Displaystyle п \, \!>
п я о — 2 ⋅ п E ты знак равно 0 <\ displaystyle n _ <\ rm
Подставляя данные (из Википедии), мы получим −0,7395 ° день −1 , значение, существенно отличное от нуля.
На самом деле, резонанс является идеальным, но он включает в себя также прецессию perijove (в точке , ближайшей к Юпитеру) . Правильное уравнение (часть уравнений Лапласа): ω ˙ <\ displaystyle <\ dot <\ omega>>>
п я о — 2 ⋅ п E ты + ω ˙ я о знак равно 0 <\ displaystyle n _ <\ rm
Другими словами, среднее движение Ио действительно вдвое больше, чем у Европы, с учетом прецессии перийова. Наблюдатель, сидящий на (дрейфующем) перийове, увидит, как луны соединяются в одном и том же месте (удлинение). Другие пары, перечисленные выше, удовлетворяют тому же типу уравнения, за исключением резонанса Мимаса-Тетиса. В этом случае резонанс удовлетворяет уравнению
4 ⋅ п Т е — 2 ⋅ п M я — Ω ˙ Т е — Ω ˙ M я знак равно 0 <\ displaystyle 4 \ cdot n _ <\ rm
Точка соединения колеблется вокруг средней точки между узлами двух лун.
Лапласовский резонанс
Резонанс Лапласа с участием Ио – Европы – Ганимеда включает следующее соотношение, фиксирующее орбитальную фазу спутников:
Φ L знак равно λ я о — 3 ⋅ λ E ты + 2 ⋅ λ грамм а знак равно 180 ∘ <\ displaystyle \ Phi _
где — средние долготы лун (второй знак равенства не учитывает либрацию). λ <\ displaystyle \ lambda>
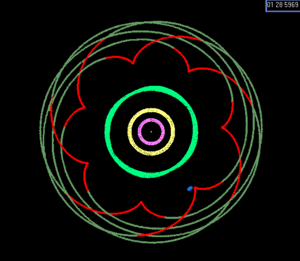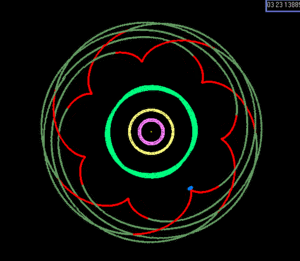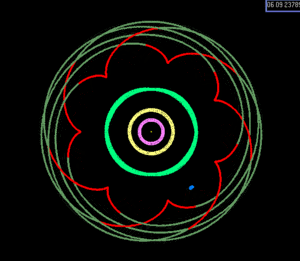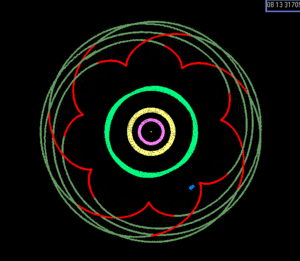
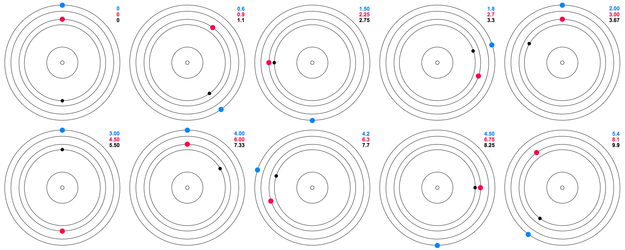
Это соотношение делает тройное соединение невозможным. (Резонанс Лапласа в системе Gliese 876 , напротив, связан с одним тройным соединением на орбиту самой удаленной планеты, игнорируя либрацию.) График показывает положения лун после 1, 2 и 3 периодов Ио. либрат около 180 ° с амплитудой 0,03 °. Φ L <\ displaystyle \ Phi _
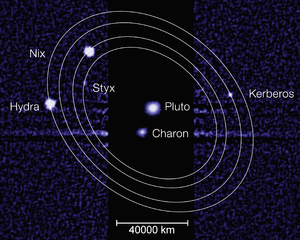
Другой «подобный Лапласу» резонанс связан со спутниками Стикс , Никс и Гидра Плутона:
Φ знак равно 3 ⋅ λ S — 5 ⋅ λ N + 2 ⋅ λ ЧАС знак равно 180 ∘ <\ displaystyle \ Phi = 3 \ cdot \ lambda _ <\ rm > — 5 \ cdot \ lambda _ <\ rm
Это отражает периоды обращения Стикса, Никса и Гидры соответственно, которые близки к соотношению 18:22:33 (или, с точки зрения близких резонансов с периодом Харона, 3 + 3/11: 4: 6; см. Ниже. ); соответствующее соотношение орбит — 11: 9: 6. Исходя из соотношений синодических периодов , существует 5 соединений Стикса и Гидры и 3 соединения Никса и Гидры на каждые 2 соединения Стикса и Никса. Как и в случае галилеевского спутникового резонанса, тройные конъюнкции запрещены. либрирует около 180 ° с амплитудой не менее 10 °. Φ <\ displaystyle \ Phi>
Плютино-резонансы
Карликовая планета Плутон движется по орбите в сети резонансов с Нептуном . К резонансам относятся:
- Резонанс среднего движения 2: 3
- Резонанс перигелия ( либрация около 90 °), удерживающий перигелий выше эклиптики
- Резонанс долготы перигелия относительно долготы Нептуна
Одним из следствий этих резонансов является то, что при пересечении Плутона орбиты Нептуна сохраняется разделение не менее 30 а.е. Минимальное расстояние между двумя телами в целом составляет 17 а.е., а минимальное расстояние между Плутоном и Ураном составляет всего 11 а.е. ( подробное объяснение и графики см. В орбите Плутона ).
Следующим по величине телом в подобном 2: 3 резонансе с Нептуном, называемым плутино , является вероятная карликовая планета Оркус . Орбита Оркуса по наклонению и эксцентриситету похожа на орбиту Плутона. Однако их взаимный резонанс с Нептуном заставляет их всегда находиться в противоположных фазах своих орбит; Поэтому Оркус иногда называют «анти-Плутоном».
Наяда: резонанс Thalassa 73:69
Самая внутренняя луна Нептуна, Наяда , находится в резонансе четвертого порядка 73:69 со следующей внешней луной, Талассой . Обращаясь к Нептуну, более наклонная Наяда последовательно проходит Талассу дважды сверху, а затем дважды снизу, в цикле, который повторяется каждые
21,5 земных суток. Две луны находятся на расстоянии около 3540 км друг от друга. Хотя их орбитальные радиусы различаются всего на 1850 км, Наяда колеблется на
2800 км выше или ниже орбитальной плоскости Таласса при самом близком сближении. Как обычно, этот резонанс стабилизирует орбиты за счет максимального разделения при соединении, но это необычно для той роли, которую играет наклон орбиты в облегчении этого избегания в случае, когда эксцентриситет минимален.
Резонансы среднего движения между планетами вне Солнечной системы
В то время как в большинстве обнаруженных внесолнечных планетных систем не было обнаружено планет в резонансах среднего движения, были обнаружены цепочки до пяти резонансных планет и до семи по крайней мере близких к резонансным планетам. Моделирование показало, что во время формирования планетной системы появлению резонансных цепочек планетарных зародышей способствует наличие первичного газового диска . Как только этот газ рассеивается, 90–95% этих цепочек должны стать нестабильными, чтобы соответствовать низкой частоте наблюдаемых резонансных цепочек.
- Как упоминалось выше, Gliese 876 e, b и c находятся в резонансе Лапласа с соотношением периодов 4: 2: 1 (124,3, 61,1 и 30,0 дней). В этом случае либрат имеет амплитуду 40 ° ± 13 °, а резонанс подчиняется усредненному по времени соотношению: Φ L <\ displaystyle \ Phi _
>
Φ L знак равно λ c — 3 ⋅ λ d + 2 ⋅ λ е знак равно 0 ∘ <\ displaystyle \ Phi _
- Кеплер-223 имеет четыре планеты в резонансе с соотношением орбит 8: 6: 4: 3 и соотношением периодов 3: 4: 6: 8 (7,3845, 9,8456, 14,7887 и 19,7257 дней). Это первый подтвержденный орбитальный резонанс с четырьмя телами. Либрации в этой системе таковы, что близкие встречи между двумя планетами происходят только тогда, когда другие планеты находятся на удаленных частях своих орбит. Моделирование показывает, что эта система резонансов должна была образоваться в результате миграции планет .
- Kepler-80 d, e, b, c и g имеют периоды в соотношении
1.000: 1.512: 2.296: 3.100: 4.767 (3.0722, 4.6449, 7.0525, 9.5236 и 14.6456 дней). Однако в системе отсчета, которая вращается вместе с соединениями, это сокращается до отношения периодов 4: 6: 9: 12: 18 (отношение орбиты 9: 6: 4: 3: 2). Соединения d и e, e и b, b и c, а также c и g происходят с относительными интервалами 2: 3: 6: 6 (9,07, 13,61 и 27,21 дня) в схеме, которая повторяется примерно каждые 190,5 дней (семь полных дней). циклов во вращающейся системе отсчета) в инерционной или невращающейся системе отсчета (эквивалентно резонансу с соотношением орбит 62: 41: 27: 20: 13 в невращающейся системе отсчета, поскольку конъюнкции циркулируют в направлении, противоположном орбитальному движению). Либрации возможных трехчастичных резонансов имеют амплитуды всего около 3 градусов, и моделирование показывает, что резонансная система устойчива к возмущениям. Тройных союзов не бывает.
TOI-178 имеет 6 подтвержденных планет, из которых 5 внешних планет образуют аналогичную резонансную цепь во вращающейся системе отсчета, которая может быть выражена как 2: 4: 6: 9: 12 в соотношении периодов или как 18: 9: 6: 4: 3 в соотношении орбиты. Кроме того, самая внутренняя планета b с периодом 1,91d по орбитам, близким к тому месту, где она также будет частью той же цепи резонанса Лапласа, поскольку резонанс 3: 5 с планетой c будет выполняться с периодом1,95d, что означает, что он мог развиться там, но вырвался из резонанса, возможно, из-за приливных сил.
- Семь планет TRAPPIST-1 размером примерно с Землю находятся в цепочке близких к резонансам (самая длинная из известных цепей), имеющих отношение орбит примерно 24, 15, 9, 6, 4, 3 и 2 или ближайших соседей. отношения периодов (в направлении наружу) около 8/5, 5/3, 3/2, 3/2, 4/3 и 3/2 (1,603, 1,672, 1,506, 1,509, 1,342 и 1,519). Они также сконфигурированы так, что каждая тройка соседних планет находится в резонансе Лапласа (то есть b, c и d в одной такой конфигурации Лапласа; c, d и e в другой и т. Д.). Ожидается, что резонансная конфигурация будет стабильной в течение миллиардов лет, если предположить, что она возникла во время планетарной миграции. Дана музыкальная интерпретация резонанса.
- Кеплер-29 имеет пару планет в резонансе 7: 9 (соотношение 1 / 1,28587).
- Кеплер-36 имеет пару планет, близких к резонансу 6: 7.
- Kepler-37 d, c и b находятся в пределах одного процента резонанса с соотношением орбит 8:15:24 и соотношением периодов 15: 8: 5 (39,792187, 21,301886 и 13,367308 дней).
- Из восьми известных планет Кеплера-90 отношения периодов b: c, c: i и i: d близки к 4: 5, 3: 5 и 1: 4 соответственно (4: 4.977, 3: 4.97 и 1 : 4.13), а d, e, f, g и h близки к соотношению периодов 2: 3: 4: 7: 11 (2: 3.078: 4.182: 7.051: 11.102; также 7: 11.021). f, g и h также близки к соотношению периодов 3: 5: 8 (3: 5,058: 7,964). Применительно к системам, подобным этой и системе Kepler-36 , расчеты показывают, что присутствие внешней газовой планеты-гиганта способствует образованию плотно упакованных резонансов между внутренними суперземлями.
- HD 41248 имеет пару суперземель в пределах 0,3% резонанса 5: 7 (соотношение 1 / 1,39718).
- K2-138 имеет 5 подтвержденных планет в непрерывной резонансной цепочке, близкой к 3: 2 (с периодами 2,353, 3,560, 5,405, 8,261 и 12,758 дня). Система была обнаружена в рамках гражданского научного проекта Exoplanet Explorers с использованием данных K2. К2-138 мог принимать коорбитальные тела (в резонансе среднего движения 1: 1). Резонансные цепные системы могут стабилизировать коорбитальные тела, и специальный анализ кривой блеска K2 и лучевой скорости с помощью HARPS может их выявить. Последующие наблюдения с помощью космического телескопа Спитцера показывают, что шестая планета продолжает резонансную цепочку 3: 2, оставляя в ней два промежутка (ее период составляет 41,97 дня). Эти пробелы могут быть заполнены более мелкими непереходящими планетами. Будущие наблюдения с помощью CHEOPS позволят измерить вариации времени прохождения системы для дальнейшего анализа массы планет и потенциально могут найти другие планетные тела в системе.
- K2-32 имеет четыре планеты в близком резонансе 1: 2: 5: 7 (с периодами 4,34, 8,99, 20,66 и 31,71 дня). Планета e имеет радиус, почти идентичный радиусу Земли. Остальные планеты имеют размер между Нептуном и Сатурном.
- V1298 Тельца имеет четыре подтвержденных планеты, из которых планеты c, d и b находятся вблизи резонанса 1: 2: 3 (с периодами 8,25, 12,40 и 24,14 дня). Планета e показывает только один транзит на кривой блеска K2 и имеет период более 36 дней. Планета e может находиться в резонансе низкого порядка (2: 3, 3: 5, 1: 2 или 1: 3) с планетой b. Система очень молода (23 ± 4 млн лет ) и может быть предшественником компактной многопланетной системы. Резонанс 2: 3 предполагает, что некоторые близкие планеты могут образовываться в резонансах или эволюционировать в них за время менее 10 млн лет. Планеты в системе имеют размер между Нептуном и Сатурном. Только планета b имеет размер, подобный Юпитеру.
- HD 158259 содержит четыре планеты в цепочке близких к резонансу 3: 2 (с периодами 3,432, 5,198, 7,954 и 12,03 дня или соотношениями периодов 1,51, 1,53 и 1,51 соответственно), с возможной пятой планетой также вблизи 3: 2 резонансный (с периодом 17,4 суток). Экзопланеты были обнаружены спектрографом SOPHIE échelle с использованием метода лучевых скоростей .
- Кеплер-1649 содержит две планеты размером с Землю, близкие к резонансу 9: 4 (с периодами 19,53527 и 8,689099 дней, или с соотношением периодов 2,24825), включая одну ( «с» ) в обитаемой зоне. Необнаруженная планета с периодом в 13 дней создаст резонансную цепочку 3: 2.
- Кеплер-88 имеет пару внутренних планет, близких к резонансу 1: 2 (отношение периодов 2,0396), с отношением масс
22,5, что приводит к очень большим колебаниям времени прохождения
0,5 дня для самой внутренней планеты. На орбите около 1400 дней находится еще более массивная внешняя планета.
Случаи внесолнечных планет, близких к резонансу среднего движения 1: 2, довольно распространены. Сообщается, что шестнадцать процентов систем, обнаруженных с помощью метода транзита , имеют такой пример (с отношениями периодов в диапазоне 1,83–2,18), а также одна шестая планетных систем, охарактеризованных доплеровской спектроскопией (в данном случае с более узким отношением периодов. диапазон). Из-за неполного знания систем фактические пропорции, вероятно, будут выше. В целом, около трети систем с характеристиками лучевой скорости, по-видимому, имеют пару планет, близких к соизмеримости . Для пар планет гораздо более характерно иметь отношение орбитальных периодов на несколько процентов больше, чем отношение резонансов среднего движения, чем на несколько процентов меньше (особенно в случае резонансов первого порядка, в которых целые числа в соотношении отличаются на единицу). ). Это предсказывалось в случаях, когда приливные взаимодействия со звездой значительны.
Совпадающие «близкие» отношения среднего движения
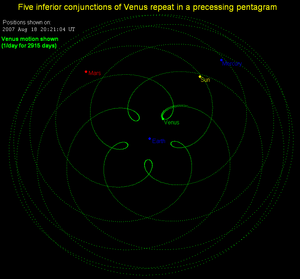
Ряд ближне- чисел на слагаемые -ratio отношений между орбитальными частотами планет или крупных спутников иногда отмечали (см список ниже). Однако они не имеют динамического значения, потому что нет соответствующей прецессии перигелия или другой либрации, чтобы сделать резонанс идеальным (см. Подробное обсуждение в разделе выше ). Такие близкие резонансы динамически несущественны, даже если рассогласование довольно мало, потому что (в отличие от истинного резонанса) после каждого цикла относительное положение тел смещается. При усреднении по астрономически коротким временным масштабам их относительное положение случайно, как и тела, которые далеки от резонанса. Например, рассмотрим орбиты Земли и Венеры, которые достигают почти одинаковой конфигурации после 8 орбит вокруг Земли и 13 орбит Венеры. Фактическое соотношение составляет 0,61518624, что всего на 0,032% отличается от точного значения 8:13. Несоответствие через 8 лет составляет всего 1,5 ° орбитального движения Венеры. Тем не менее, этого достаточно, чтобы Венера и Земля оказывались в противоположной относительной ориентации по отношению к оригиналу каждые 120 таких циклов, что составляет 960 лет. Следовательно, на шкале времени в тысячи лет и более (все еще крошечной по астрономическим стандартам) их относительное положение фактически случайно.
Присутствие близкого резонанса может отражать то, что идеальный резонанс существовал в прошлом, или что система развивается в сторону резонанса в будущем.
Некоторые совпадения орбитальной частоты включают:
| (Соотношение) и тела | Несоответствие после одного цикла | Время рандомизации | Вероятность |
|---|---|---|---|
| Планеты | |||
| (9:23) Венера — Меркурий | 4,0 ° | 200 г | 0,19 |
| (8:13) Земля — Венера | 1,5 ° | 1000 г | 0,065 |
| (243: 395) Земля — Венера | 0,8 ° | 50000 лет | 0,68 |
| (1: 3) Марс — Венера | 20,6 ° | 20 лет | 0,11 |
| (1: 2) Марс — Земля | 42,9 ° | 8 лет | 0,24 |
| (1:12) Юпитер — Земля | 49,1 ° | 40 лет | 0,28 |
| (2: 5) Сатурн — Юпитер | 12,8 ° | 800 лет | 0,13 |
| (1: 7) Уран — Юпитер | 31,1 ° | 500 лет | 0,18 |
| (7:20) Уран — Сатурн | 5,7 ° | 20000 лет | 0,20 |
| (5:28) Нептун — Сатурн | 1.9 ° | 80 000 лет | 0,052 |
| (1: 2) Нептун — Уран | 14,0 ° | 2000 г | 0,078 |
| Система Марса | |||
| (1: 4) Деймос — Фобос | 14,9 ° | 0,04 года | 0,083 |
| Основные астероиды | |||
| (1: 1) Паллада — Церера | 0,7 ° | 1000 лет | 0,0039 |
| (7:18) Юпитер — Паллада | 0,10 ° | 100000 лет | 0,0040 |
| 87 Система Сильвии | |||
| (17:45) Ромул — Рем | 0,7 ° | 40 лет | 0,067 |
| Система Юпитера | |||
| (1: 6) Ио — Метис | 0,6 ° | 2 года | 0,0031 |
| (3: 5) Амальтея — Адрастея | 3,9 ° | 0,2 года | 0,064 |
| (3: 7) Каллисто — Ганимед | 0,7 ° | 30 лет | 0,012 |
| Система Сатурна | |||
| (2: 3) Энцелад — Мимас | 33,2 ° | 0,04 года | 0,33 |
| (2: 3) Диона — Тетис | 36,2 ° | 0,07 года | 0,36 |
| (3: 5) Рея — Диона | 17,1 ° | 0,4 года | 0,26 |
| (2: 7) Титан — Рея | 21,0 ° | 0,7 года | 0,22 |
| (1: 5) Япет — Титан | 9,2 ° | 4 года | 0,051 |
| Крупные кентавры | |||
| (3: 4) Уран — Харикло | 4.5 ° | 10 000 лет | 0,073 |
| Система урана | |||
| (3: 5) Розалинда — Корделия | 0,22 ° | 4 года | 0,0037 |
| (1: 3) Умбриэль — Миранда | 24,5 ° | 0,08 года | 0,14 |
| (3: 5) Умбриэль — Ариэль | 24,2 ° | 0,3 года | 0,35 |
| (1: 2) Титания — Умбриэль | 36,3 ° | 0,1 года | 0,20 |
| (2: 3) Оберон — Титания | 33,4 ° | 0,4 года | 0,34 |
| Система Нептуна | |||
| (1:20) Тритон — Наяда | 13,5 ° | 0,2 года | 0,075 |
| (1: 2) Протей — Лариса | 8,4 ° | 0,07 года | 0,047 |
| (5: 6) Протей — Гиппокамп | 2,1 ° | 1 год | 0,057 |
| Система Плутона | |||
| (1: 3) Стикс — Харон | 58,5 ° | 0,2 года | 0,33 |
| (1: 4) Никс — Харон | 39,1 ° | 0,3 года | 0,22 |
| (1: 5) Кербер — Харон | 9,2 ° | 2 года | 0,05 |
| (1: 6) Гидра — Харон | 6,6 ° | 3 года | 0,037 |
| Система Хаумеа | |||
| (3: 8) Хияка — Намака | 42,5 ° | 2 года | 0,55 |
Наименее вероятная орбитальная корреляция в списке — это орбитальная корреляция между Ио и Метидой, за которой следуют орбиты между Розалиндой и Корделией, Палладой и Церерой, Юпитером и Палладой, Каллисто и Ганимедом, Гидрой и Хароном соответственно.
Возможные прошлые резонансы среднего движения
Прошлый резонанс между Юпитером и Сатурном, возможно, сыграл драматическую роль в ранней истории Солнечной системы. Компьютерная модель 2004 года Алессандро Морбиделли из Обсерватории Лазурного берега в Ницце предположила, что формирование резонанса 1: 2 между Юпитером и Сатурном (из-за взаимодействий с планетезималиями, которые заставили их перемещаться внутрь и наружу, соответственно) создало гравитационный толчок, который продвинул Уран и Нептун на более высокие орбиты, а в некоторых сценариях заставил их поменяться местами, что удвоило бы расстояние Нептуна от Солнца. Возникшее в результате изгнание объектов из прото-пояса Койпера при движении Нептуна могло объяснить позднюю тяжелую бомбардировку через 600 миллионов лет после образования Солнечной системы и происхождение троянских астероидов Юпитера . Миграция Нептуна наружу может также объяснить текущую занятость некоторых из его резонансов (особенно резонанса 2: 5) в пределах пояса Койпера.
В то время как спутники Сатурна среднего размера Диона и Тетис сейчас не близки к точному резонансу, они, возможно, находились в резонансе 2: 3 в начале истории Солнечной системы. Это могло бы привести к эксцентриситету орбиты и приливному нагреву, который, возможно, достаточно нагрел внутренность Тетиса, чтобы сформировать подземный океан. Последующее замерзание океана после того, как луны ускользнули из резонанса, могло вызвать напряжения растяжения, которые создали огромную систему грабенов Итака Хазма на Тетисе.
Спутниковая система Урана заметно отличается от систем Юпитера и Сатурна тем, что в ней отсутствуют точные резонансы между более крупными лунами, в то время как большинство более крупных спутников Юпитера (3 из 4 крупнейших) и Сатурна (6 из 8 крупнейших спутников) ) находятся в резонансах среднего движения. Во всех трех спутниковых системах луны, вероятно, были захвачены в резонансы среднего движения в прошлом, поскольку их орбиты смещались из-за приливной диссипации (процесса, при котором спутники получают орбитальную энергию за счет энергии вращения первичной звезды, непропорционально влияя на внутренние спутники). В системе Урана, однако, из-за меньшей степени сжатия планеты и большего относительного размера ее спутников выйти из резонанса среднего движения намного проще. Более низкое сжатие первичной обмотки изменяет ее гравитационное поле таким образом, что различные возможные резонансы располагаются более близко друг к другу. Чем больше относительный размер спутников, тем сильнее их взаимодействие. Оба фактора приводят к более хаотическому орбитальному поведению при резонансах среднего движения или вблизи них. Выход из резонанса может быть связан с захватом во вторичный резонанс и / или вызванным приливной эволюцией увеличением эксцентриситета или наклона орбиты .
Резонансы среднего движения, которые, вероятно, когда-то существовали в системе Урана, включают (3: 5) Ариэль-Миранду, (1: 3) Умбриэль-Миранду, (3: 5) Умбриэль-Ариэль и (1: 4) Титанию-Ариэль. Доказательства таких прошлых резонансов включают относительно высокие эксцентриситет орбит внутренних спутников Урана и аномально высокое наклонение орбиты Миранды. Высокие эксцентриситеты орбиты в прошлом, связанные с резонансами (1: 3) Умбриэль-Миранда и (1: 4) Титания-Ариэль, могли привести к приливному нагреву внутренних частей Миранды и Ариэля, соответственно. Миранда, вероятно, вышла из своего резонанса с Умбриэлем через вторичный резонанс, и считается, что механизм этого побега объясняет, почему ее орбитальное наклонение более чем в 10 раз превышает наклонение орбиты других регулярных спутников Урана (см. Естественные спутники Урана ).
Как и в случае с Мирандой, нынешние наклоны лун Юпитера Амальтеи и Фивы считаются указанием на прошлое прохождение через резонансы 3: 1 и 4: 2 с Ио соответственно.
Полагают, что обычные спутники Нептуна Протей и Лариса прошли через резонанс 1: 2 несколько сотен миллионов лет назад; с тех пор луны отдалились друг от друга, потому что Протей находится за пределами синхронной орбиты, а Лариса — внутри одной. Считается, что прохождение через резонанс возбудило эксцентриситет обеих лун до такой степени, которая с тех пор не была полностью подавлена.
В случае спутников Плутона было высказано предположение, что нынешние близкие резонансы являются пережитками предыдущего точного резонанса, который был нарушен приливным затуханием эксцентриситета орбиты Харона (подробнее см . Естественные спутники Плутона ). Ближний резонанс может поддерживаться 15% -ной локальной флуктуацией гравитационного поля Плутон-Харон. Таким образом, эти близкие резонансы могут быть не случайными.
Меньшая внутренняя луна карликовой планеты Хаумеа , Намака , составляет одну десятую массы большей внешней луны Хииаки . Намака обращается вокруг Хаумеа за 18 дней по эксцентрической, не кеплеровской орбите, и по состоянию на 2008 год наклонена на 13 ° от Хииаки. В масштабе времени системы она должна была приливно затухать на более круговую орбиту. Похоже, что он был возмущен резонансами с более массивным Хияка из-за сходящихся орбит, когда он двигался наружу от Хаумеа из-за приливной диссипации. Спутники могли быть захвачены, а затем несколько раз выходили из орбитального резонанса. Они, вероятно, прошли через резонанс 3: 1 относительно недавно и в настоящее время находятся в резонансе 8: 3 или, по крайней мере, близки к нему. Орбита Намаки сильно возмущена , с текущей прецессией около -6,5 ° в год.
Источник