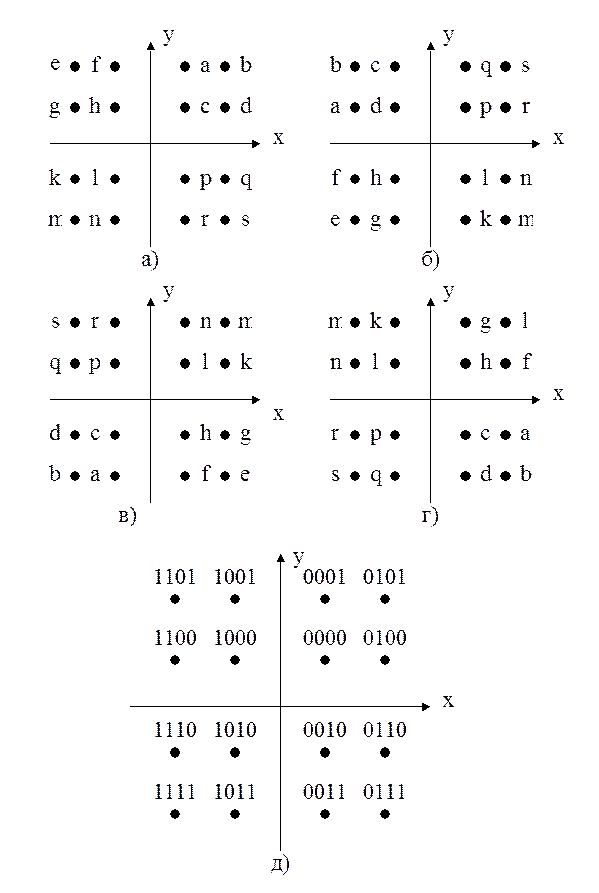Сигнальное созвездие для кам 16

Квадратурная амплитудная модуляция , страница 6

Если бы частота и фаза опорного генератора точно совпадала с частотой и фазой несущего сигнала, то при передаче информации каждый детектированный символ соответствовал бы точному сочетанию амплитуды и фазы одного из 16 возможных состояний (т.е. всегда «попадал» бы в одну из точек созвездия на рис. 20.13).

Если же частота опорного генератора не равна требуемой, то все созвездия в системе координат Q – I как бы «вращается» с частотой, равной разности частот несущей и опорного генератора.

Если же не совпадают начальные фазы, то даже при равенстве частот созвездие окажется пусть неподвижным, но повернутым относительно своего правильного положения на какой-то произвольный случайный угол.

Поскольку перед началом подстройки ни фаза, ни частота опорного генератора не совпадают с требуемыми, то в начале созвездие всегда вращается, причем направление вращения заранее неизвестно. В задачу входит, анализируя особенности этого вращения, замедлить его и остановить в таком положении, чтобы созвездие остановилось максимально близко от своего правильного положения.

Это производится следующим образом. Как следует из правила демодуляции, решение о том, что передавалось какое-то одно конкретное состояние из 16 возможных принимается, когда амплитудно-фазовое состояние входного сигнала (или, что то же самое, соотношение величин ортогональных сигналов Q и I) попадает в некоторую область вблизи одной из точек созвездия.

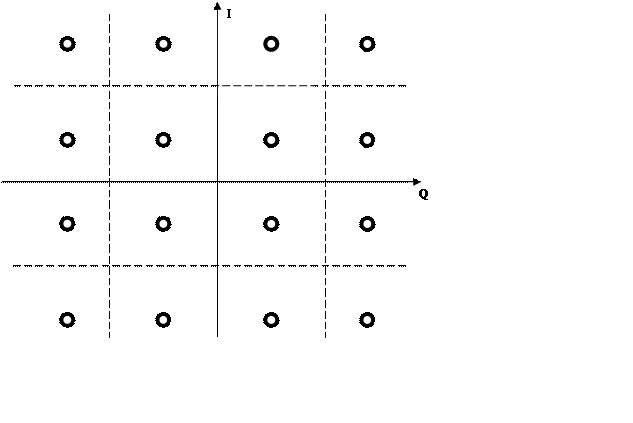Рис. 20.13. Сигнальное созвездие при КАМ-16

Исходя из соображений максимальной помехоустойчивости, границу между соседними областями располагают на одинаковом расстоянии между соседними точками созвездия. В результате эти области приобретают вид, показанный на рис. 20.13.

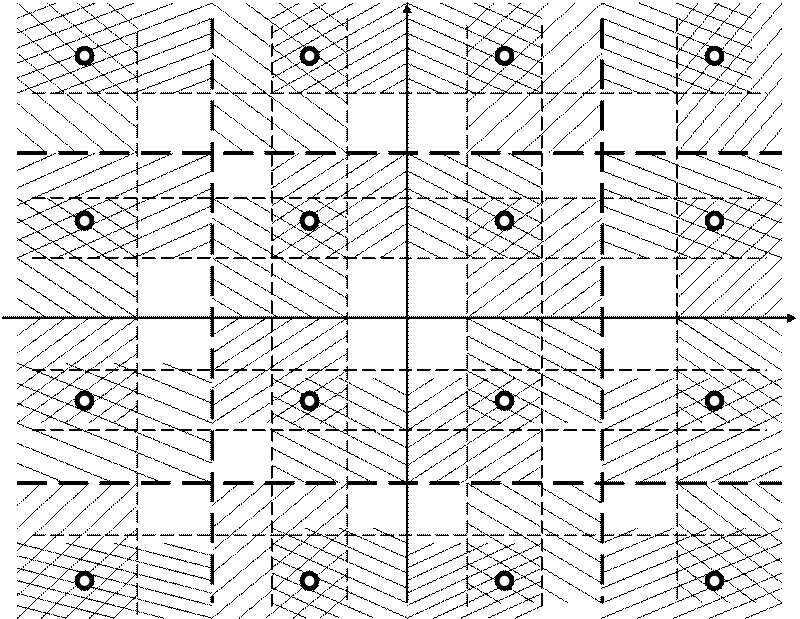
При реакции описываемого алгоритма подстройки с помощью соответствующих АЦП плоскость Q и I разбивается на большее число зон. (Размеры более мелких зон будут анализироваться дальше). Конфигурация новых мелких зон приведена на рис. 20.14.

Все зоны разделим на 4 группы:

1. Зоны, в которых находятся точки созвездия (зоны с) – заштрихованы двойной штриховкой.

2. Зоны а в которые попадает какая-либо точка, ранее присутствующая в зоне с, при повороте созвездия по часовой стрелки (из любого место зоны с) при пересечении границы зоны с – обозначены косой штриховкой (/////).

3. Зоны в, в которые переместится любая точка из зоны с, пересекая ее границу при повороте созвездия против часовой стрелки. Обозначены косой штриховкой (\\\\\).

4. Зоны d, в которые из зоны с при любом повороте созвездия точка попасть не может. Они в операциях алгоритма подстройки не задействованы. Штриховка отсутствует.

Рис. 20.14. Зоны созвездия КАМ-16

Рассмотрим работу алгоритмов. Если в какой-то момент «рабочая» точка присутствовала в зоне, принадлежащей какой-либо из 4 групп, то при приходе следующего полубайта она перескочит в другое место плоскости Q — I, но попадает в зону, принадлежащую той же группе, т.е. имеет, по сути, всего 4 зоны – а, в, с, d. Поэтому мы все зоны, принадлежащие одной группе, будем считать одной зоной, тем более, что действия алгоритма определяется именно переходом из зоны в зону.

Пока подстройка не произведена, созвездие непрерывно вращается, и в каждый момент времени амплитудно-фазовые соотношения принимают одно из 16 состояний.

При непрерывном вращении в какой-то момент времени текущее положение («рабочая» точка) попадает в зону с. При этом включается режим ожидания.

Он длится до тех пор, пока в результате вращения, точка после пересечения границы зоны с не переместится или в зону а или в зону в. После этого включается режим шаговой перестройки.

Если «рабочая» точка переместилась в зону а, это означает, что частота опорного генератора меньше частоты несущей, и ее надо увеличивать. При этом вырабатывается управляющий сигнал, увеличивающий на определенный шаг частоту опорного генератора.

Если точка из зоны с переместилась в зону в, это означает, что частота опорного генератора больше несущей частоты и ее надо уменьшать. При этом вырабатывается управляющий частоту опорного генератора на определенный шаг.

Источник

Квадратурная амплитудная модуляция , страница 3

На втором этапе фазовый сдвиг подстраивается таким образом, чтобы те амплитудно-фазовые сочетания, которые наблюдаются в выходных сигналах этого блока (I₂ и Q₂), были расположены симметрично относительно осей X и Y.

Однако при этом сигналы I₂, Q₂ могут соответствовать как истинным A_C, A_S, так и любой из трех возможных ошибочных ситуаций (рис. 28,б — г). Поэтому в следующем блоке производится их идентификация с «правильными» (A_C, A_S). В последнем блоке на основании текущего сочетания уровней сигналов (A_C, A_S) производится декодирование, т.е. восстановление принятого полубайта.

Рис. 20.5. Варианты сигнального созвездия КАМ-16

Для частотно-фазовой подстройки здесь невозможно использовать обычные схемы ФАПЧ из-за присутствия амплитудно-фазовой манипуляции информационным сигналом. Чтобы использовать ФАПЧ должна иметься возможность в каждый момент времени измерять фазовый сдвиг между входным сигналом и сигналом перестраиваемого генератора, чтобы определить, в какую сторону необходимо изменять его частоту. Поскольку при разности частот значение фазового сдвига изменяется достаточно быстро (он непрерывно растет или падает со скоростью Δω), то его измерение также необходимо производить быстро (за малый интервал времени).

Рис. 20.6. Укрупненная структурная схема демодулятора КАМ

А в ситуации наложения на несущую частоту амплитудно-фазовой манипуляции от её влияния можно избавиться только усредняя результат измерения на большом интервале времени. При этом считается, что все М передаваемых состояний равновероятны и долговременное усреднение сведет их влияние к нулю.

Однако при таком долговременном усреднении измерение текущего постоянно меняющегося фазового сдвига между промежуточной частотой входного сигнала и частотой ГУН невозможно. В связи с этим, подстройка частоты и подстройка фазы в приёмном устройстве M-QAM производится раздельно и в этих целях используются различные принципы.

Структурная схема блока подстройки частоты приведена на рис. 20.7. Сигнал промежуточной частоты в одном из перемножителей умножается на сигнал ГУН непосредственно, а в другом – на сигнал ГУН, пропущенный через фазовращатель на 90 0 . Далее после прохождения через фильтры низкой частоты (Ф), формируются квадратурные сигналы I₁ и Q₁.

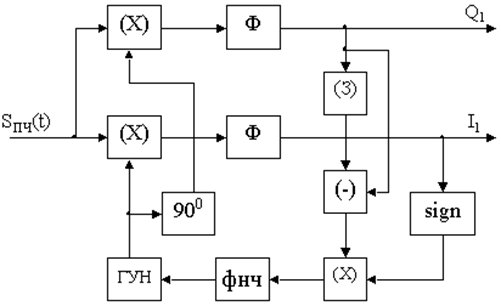Рис. 20.7. Устройство подстройки частоты приёмника сигналов КАМ

Предварительно будем считать, что амплитудно-фазовая манипуляция из-за передачи информационных сообщений отсутствует. Тогда, если оба вектора расположены в правом верхнем квадранте плоскости, то Q₁(t₂) > Q₁(t₁). То же самое справедливо и для правого нижнего квадранта. Если бы оба вектора были бы расположены в левой полуплоскости, то такое же вращение вектора А против часовой стрелки соответствовало бы случаю Q₁(t₂) 3 4 5 6 7 8 9 10 11

Источник

Квадратурная модуляция (QAM)

Для увеличения скорости передачи данных используют так называемую квадратурную амплитудную модуляцию QAM, которая является амплитудно-фазовым видом модуляции. QAM применяется в кабельных модемах, в стандарте цифрового телевидения DVB-C, а также, в цифровом радиовещании СВЧ диапазона.

С точки зрения скорости передачи этот вид модуляции намного более эффективен по сравнению с двоичной (BPSK), четырехпозиционной (QPSK) или восьмипозиционной (8-PSK) фазовой модуляцией. Следует сразу оговориться, что QPSK и 4-QAM на самом деле один и тот же вид модуляции.

В 16-позиционной QAM (16-QAM) существует по четыре сигнальных значения для каждой из квадратурных компонент I и Q. Этим достигаются шестнадцать значений суммарного сигнала.

Зная, что , получаем, что в 16-QAM одним символом могут быть переданы четыре бита. Это означает, что символьная скорость в таком виде модуляции получается в четыре раза меньше битовой, т. е. равна 1/4 от битовой скорости. Таким образом, данный тип модуляции позволяет организовать спектрально более эффективную передачу данных. Векторная диаграмма сигнала 16-QAM приведена на рисунке 1.

Рисунок 1. Векторная диаграмма сигнала 16-QAM

Точно так же, как и в других системах модуляции в 16-QAM применяется кодирование Грея. Соответствие сигнальных созвездий, кода Грея и цифровых значений сигналов I и Q для 16-QAM, приведено на рисунке 2.

Рисунок 2. Соответствие сигнальных созвездий, кода Грея и цифровых значений сигналов I и Q для 16-QAM

Глазковая диаграмма сигналов I и Q для 16-позиционной квадратурной модуляции 16 QAM приведена на рисунке 3.

Рисунок 3. Глазковая диаграмма сигналов I и Q 16-позиционной квадратурной модуляции 16 QAM

В 16-ти позиционной QAM (16-QAM) существует по четыре сигнальных значения для каждой из квадратурных компонент I и Q. Этим достигаются 16 значений суммарного сигнала.

Для иллюстрации, на рисунке 4 приведена фотография экрана измерительного прибора — векторного анализатора. На этом рисунке видны векторная, глазковая диаграмма и основные характеристики сигнала 16-QAM на частоте 450 МГц.

Рисунок 4. Экран векторного анализатора, на котором видны векторная, глазковая диаграмма и основные характеристики сигнала 16-QAM на частоте 450 МГц

Еще одна разновидность QAM — это 32-QAM. Ее характеристики таковы: по шесть сигнальных значений для I и для Q, что в итоге дает точек созвездия для суммарного сигнала. Сигнальное созвездие сигнала 32-QAM приведено на рисунке 5.

Рисунок 5. Сигнальное созвездие сигнала 32-QAM

Этот тип модуляции наделен особенностью. В итоге, количество значений 36 не соответствует исходным данным, т.к. слишком велико, (). Поэтому, четыре «угловых» сигнальных значения, (на которые приходится большинство мощности передатчика), опущены. Этим уменьшается значение выходной мощности, которую должен генерировать передатчик. Исходя из того, что , получаем битовую скорость, равную 5 бит/с и символьную скорость, равную 1/5.

Особенность сигналов QAM — это возможность увеличивать количество сигнальных точек в обмен на помехоустойчивость. В результате в одной и той же полосе сигналов есть возможность увеличивать скорость передачи цифровой информации. Ограничение на увеличение пропускной способности канала накладывает только сложность реализации аппаратуры телекоммуникационных устройств

Дата последнего обновления файла 31.01.2020

Понравился материал? Поделись с друзьями!

1. Steve C. Cripps RF Power Amplifiers for Wireless Communications — ARTECH HOUSE, INC., 2006
2. Marian K. Kazimierczuk RF Power Amplifiers — John Wiley & Sons, Ltd 2008
3. Радиопередающие устройства: учебник для ВУЗов; под ред. В. В. Шахгильдяна. — 3-е изд., перераб. и доп. — М.: Радио и связь, 2003.

Вместе со статьей «Квадратурная модуляция (QAM)» читают:

MSK-модуляция частотная с минимальным сдвигом по частоте
https://digteh.ru/UGFSvSPS/modul/MSK/

Автор Микушин А. В. All rights reserved. 2001 . 2020

Предыдущие версии сайта:
http://neic.nsk.su/

Об авторе:
к.т.н., доц., Александр Владимирович Микушин

Кандидат технических наук, доцент кафедры САПР СибГУТИ. Выпускник факультета радиосвязи и радиовещания (1982) Новосибирского электротехнического института связи (НЭИС).

А.В.Микушин длительное время проработал ведущим инженером в научно исследовательском секторе НЭИС, конструкторско технологическом центре «Сигнал», Научно производственной фирме «Булат». В процессе этой деятельности он внёс вклад в разработку систем радионавигации, радиосвязи и транкинговой связи.

Научные исследования внедрены в аппаратуре радинавигационной системы Loran-C, комплексов мобильной и транкинговой связи «Сигнал-201», авиационной системы передачи данных «Орлан-СТД», отечественном развитии системы SmarTrunkII и радиостанций специального назначения.

Источник

Сигнальные созвездия QAM и векторная диаграмма

В предыдущих статьях рассматривались виды модуляций амплитудная и фазовая, спектр действительного сигнала, рекомендую почитать статью.

p, blockquote 1,0,0,0,0 —>

p, blockquote 2,0,0,0,0 —>

Сигнальное созвездие и векторная диаграмма

Диаграмма сигнального созвездия или просто “созвездие” (Constellation Diagram, Constellation ) показывает положение символов на комплексной плоскости только в момент времени принятия решения о принятом символе.

p, blockquote 3,0,0,0,0 —>

Векторная диаграмма показывает перемещение вектора на комплексной плоскости от символа к символу. Существует разное отображение векторов на плоскости. Созвездие это одно из них. Для примера диаграмма ниже.

p, blockquote 4,0,0,0,0 —>

p, blockquote 5,0,1,0,0 —>

Каждая точка это, то место, где заканчивается вектор. Линия это тоже, то место, где заканчивается вектор. Чем они отличаются? Когда мы строим звездную диаграмму, мы берем значение сигнала, только в определенный момент времени. Это те моменты времени, когда мы должны брать выборку сигнала и принимать решение, о том, какой символ у нас был передан.

p, blockquote 6,0,0,0,0 —>

Оценка качества приема по звездной диаграмме

Что мы можем увидеть по созвездию, какие есть вредные факторы?

p, blockquote 7,0,0,0,0 —>

p, blockquote 8,0,0,0,0 —>

На картинке выше, слева показана идеальная диаграмма, для QAM16. Число 16 говорит о том, что у нас 16 точек в созвездии, а QAM — квадратурно-амплитудная модуляция. Квадратурная, потому что мы каждое значение сигнала, амплитуды и фазы задаем через координаты в виде двух квадратур I и Q. Если появился постоянный фазовый сдвиг, то созвездие повернулось. Каждый вектор повернется на один угол.

p, blockquote 9,0,0,0,0 —>

Теперь рассмотрим частотный сдвиг.

p, blockquote 10,0,0,0,0 —>

p, blockquote 11,1,0,0,0 —>

Например, принимая сигнал, до конца не восстановили частотную синхронизацию, есть ошибка, что будет с созвездием? Если есть частота, то вектор будет вращаться с этой частотой. Мы будем наблюдать, что всё созвездие начнет вращаться (картинка выше).

p, blockquote 12,0,0,0,0 —>

Справа на картинке, влияние белого шума на сигнал. Из-за шума, вектор начнет расползаться относительно своего начального положения. В разный момент времени у вектора разная амплитуда и фаза.

p, blockquote 13,0,0,0,0 —>

Рассмотрим влияние флуктуаций на сигнал. Флуктуация это случайное изменение.

p, blockquote 14,0,0,0,0 —>

p, blockquote 15,0,0,0,0 —>

Фазовая флуктуация, дрожание во времени, то по часовой, то против часовой. Если видим такую картину, как на рисунке выше, то можем сказать, что ФАПЧ в схеме работает не корректно.

p, blockquote 16,0,0,0,0 —>

Амплитудные флуктуации, вектор дрожит вдоль вектора, т.е. изменяется только амплитуда. Это может быть из-за АРУ (автоматической регулировки управления) в схеме, она не правильно работает.

p, blockquote 17,0,0,1,0 —>

Вопрос! Что будет со звездной диаграммой, если пропустим сигнал через нелинейный усилитель мощности? Характеристика показана на графике ниже, амплитуда входного и выходного сигнала.

p, blockquote 18,0,0,0,0 —>

p, blockquote 19,0,0,0,0 —>

Сначала идет линейный участок, потом характеристика ближе к напряжению питания начинает загибаться. Чем больше амплитуда входного сигнала, тем сильнее сигнал сжимается в области высоких амплитуд. Как это проявилось бы на звездной диаграмме?

p, blockquote 20,0,0,0,0 —>

p, blockquote 21,0,0,0,0 —>

Сигналы имеют разные амплитуды. Было прямоугольное созвездие, но потом, точки которые с большими амплитудами, они прижались к центру. Наибольшее искажение получили точки, которые находятся в углу, потому что у этих точек была наибольшая амплитуда.

p, blockquote 22,0,0,0,0 —> p, blockquote 23,0,0,0,1 —>

Зачем нужны круглые созвездия? Если есть необходимость пропускать сигнал через нелинейный усилитель, а нелинейный усилитель обладает большим КПД. Используют круглое созвездие, потому что все точки, находящиеся на одной окружности, испытывают равное искажение. В отличии от тех созвездий, которые имеют прямоугольную форму.

Источник