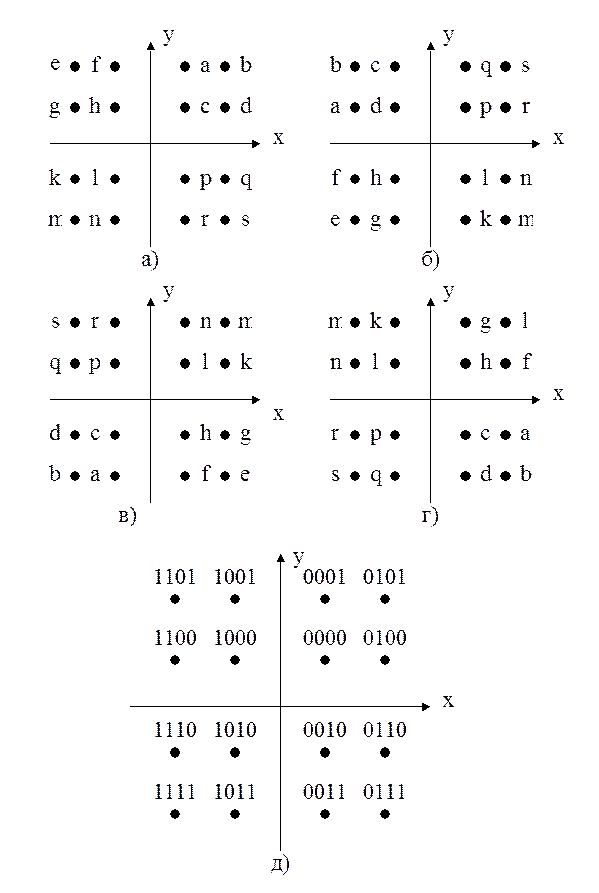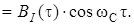Сигнальное созвездие для qam 16

Квадратурная амплитудная модуляция , страница 3

На втором этапе фазовый сдвиг подстраивается таким образом, чтобы те амплитудно-фазовые сочетания, которые наблюдаются в выходных сигналах этого блока (I₂ и Q₂), были расположены симметрично относительно осей X и Y.

Однако при этом сигналы I₂, Q₂ могут соответствовать как истинным A_C, A_S, так и любой из трех возможных ошибочных ситуаций (рис. 28,б — г). Поэтому в следующем блоке производится их идентификация с «правильными» (A_C, A_S). В последнем блоке на основании текущего сочетания уровней сигналов (A_C, A_S) производится декодирование, т.е. восстановление принятого полубайта.

Рис. 20.5. Варианты сигнального созвездия КАМ-16

Для частотно-фазовой подстройки здесь невозможно использовать обычные схемы ФАПЧ из-за присутствия амплитудно-фазовой манипуляции информационным сигналом. Чтобы использовать ФАПЧ должна иметься возможность в каждый момент времени измерять фазовый сдвиг между входным сигналом и сигналом перестраиваемого генератора, чтобы определить, в какую сторону необходимо изменять его частоту. Поскольку при разности частот значение фазового сдвига изменяется достаточно быстро (он непрерывно растет или падает со скоростью Δω), то его измерение также необходимо производить быстро (за малый интервал времени).

Рис. 20.6. Укрупненная структурная схема демодулятора КАМ

А в ситуации наложения на несущую частоту амплитудно-фазовой манипуляции от её влияния можно избавиться только усредняя результат измерения на большом интервале времени. При этом считается, что все М передаваемых состояний равновероятны и долговременное усреднение сведет их влияние к нулю.

Однако при таком долговременном усреднении измерение текущего постоянно меняющегося фазового сдвига между промежуточной частотой входного сигнала и частотой ГУН невозможно. В связи с этим, подстройка частоты и подстройка фазы в приёмном устройстве M-QAM производится раздельно и в этих целях используются различные принципы.

Структурная схема блока подстройки частоты приведена на рис. 20.7. Сигнал промежуточной частоты в одном из перемножителей умножается на сигнал ГУН непосредственно, а в другом – на сигнал ГУН, пропущенный через фазовращатель на 90 0 . Далее после прохождения через фильтры низкой частоты (Ф), формируются квадратурные сигналы I₁ и Q₁.

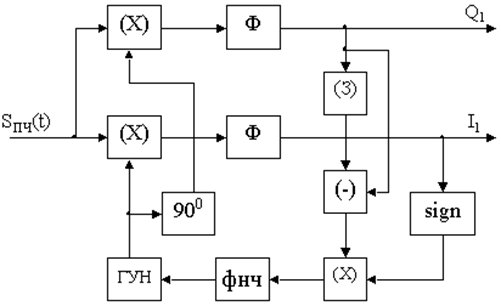Рис. 20.7. Устройство подстройки частоты приёмника сигналов КАМ

Предварительно будем считать, что амплитудно-фазовая манипуляция из-за передачи информационных сообщений отсутствует. Тогда, если оба вектора расположены в правом верхнем квадранте плоскости, то Q₁(t₂) > Q₁(t₁). То же самое справедливо и для правого нижнего квадранта. Если бы оба вектора были бы расположены в левой полуплоскости, то такое же вращение вектора А против часовой стрелки соответствовало бы случаю Q₁(t₂) 3 4 5 6 7 8 9 10 11

Источник

Квадратурная модуляция (QAM)

Для увеличения скорости передачи данных используют так называемую квадратурную амплитудную модуляцию QAM, которая является амплитудно-фазовым видом модуляции. QAM применяется в кабельных модемах, в стандарте цифрового телевидения DVB-C, а также, в цифровом радиовещании СВЧ диапазона.

С точки зрения скорости передачи этот вид модуляции намного более эффективен по сравнению с двоичной (BPSK), четырехпозиционной (QPSK) или восьмипозиционной (8-PSK) фазовой модуляцией. Следует сразу оговориться, что QPSK и 4-QAM на самом деле один и тот же вид модуляции.

В 16-позиционной QAM (16-QAM) существует по четыре сигнальных значения для каждой из квадратурных компонент I и Q. Этим достигаются шестнадцать значений суммарного сигнала.

Зная, что , получаем, что в 16-QAM одним символом могут быть переданы четыре бита. Это означает, что символьная скорость в таком виде модуляции получается в четыре раза меньше битовой, т. е. равна 1/4 от битовой скорости. Таким образом, данный тип модуляции позволяет организовать спектрально более эффективную передачу данных. Векторная диаграмма сигнала 16-QAM приведена на рисунке 1.

Рисунок 1. Векторная диаграмма сигнала 16-QAM

Точно так же, как и в других системах модуляции в 16-QAM применяется кодирование Грея. Соответствие сигнальных созвездий, кода Грея и цифровых значений сигналов I и Q для 16-QAM, приведено на рисунке 2.

Рисунок 2. Соответствие сигнальных созвездий, кода Грея и цифровых значений сигналов I и Q для 16-QAM

Глазковая диаграмма сигналов I и Q для 16-позиционной квадратурной модуляции 16 QAM приведена на рисунке 3.

Рисунок 3. Глазковая диаграмма сигналов I и Q 16-позиционной квадратурной модуляции 16 QAM

В 16-ти позиционной QAM (16-QAM) существует по четыре сигнальных значения для каждой из квадратурных компонент I и Q. Этим достигаются 16 значений суммарного сигнала.

Для иллюстрации, на рисунке 4 приведена фотография экрана измерительного прибора — векторного анализатора. На этом рисунке видны векторная, глазковая диаграмма и основные характеристики сигнала 16-QAM на частоте 450 МГц.

Рисунок 4. Экран векторного анализатора, на котором видны векторная, глазковая диаграмма и основные характеристики сигнала 16-QAM на частоте 450 МГц

Еще одна разновидность QAM — это 32-QAM. Ее характеристики таковы: по шесть сигнальных значений для I и для Q, что в итоге дает точек созвездия для суммарного сигнала. Сигнальное созвездие сигнала 32-QAM приведено на рисунке 5.

Рисунок 5. Сигнальное созвездие сигнала 32-QAM

Этот тип модуляции наделен особенностью. В итоге, количество значений 36 не соответствует исходным данным, т.к. слишком велико, (). Поэтому, четыре «угловых» сигнальных значения, (на которые приходится большинство мощности передатчика), опущены. Этим уменьшается значение выходной мощности, которую должен генерировать передатчик. Исходя из того, что , получаем битовую скорость, равную 5 бит/с и символьную скорость, равную 1/5.

Особенность сигналов QAM — это возможность увеличивать количество сигнальных точек в обмен на помехоустойчивость. В результате в одной и той же полосе сигналов есть возможность увеличивать скорость передачи цифровой информации. Ограничение на увеличение пропускной способности канала накладывает только сложность реализации аппаратуры телекоммуникационных устройств

Дата последнего обновления файла 31.01.2020

Понравился материал? Поделись с друзьями!

1. Steve C. Cripps RF Power Amplifiers for Wireless Communications — ARTECH HOUSE, INC., 2006
2. Marian K. Kazimierczuk RF Power Amplifiers — John Wiley & Sons, Ltd 2008
3. Радиопередающие устройства: учебник для ВУЗов; под ред. В. В. Шахгильдяна. — 3-е изд., перераб. и доп. — М.: Радио и связь, 2003.

Вместе со статьей «Квадратурная модуляция (QAM)» читают:

MSK-модуляция частотная с минимальным сдвигом по частоте
https://digteh.ru/UGFSvSPS/modul/MSK/

Автор Микушин А. В. All rights reserved. 2001 . 2020

Предыдущие версии сайта:
http://neic.nsk.su/

Об авторе:
к.т.н., доц., Александр Владимирович Микушин

Кандидат технических наук, доцент кафедры САПР СибГУТИ. Выпускник факультета радиосвязи и радиовещания (1982) Новосибирского электротехнического института связи (НЭИС).

А.В.Микушин длительное время проработал ведущим инженером в научно исследовательском секторе НЭИС, конструкторско технологическом центре «Сигнал», Научно производственной фирме «Булат». В процессе этой деятельности он внёс вклад в разработку систем радионавигации, радиосвязи и транкинговой связи.

Научные исследования внедрены в аппаратуре радинавигационной системы Loran-C, комплексов мобильной и транкинговой связи «Сигнал-201», авиационной системы передачи данных «Орлан-СТД», отечественном развитии системы SmarTrunkII и радиостанций специального назначения.

Источник

Формирователь модулирующих символов

1. Изобразить сигнальное созвездие для вида модуляции – КАМ-16 (квадратурная амплитудная модуляция) рис. 3.4.1..

2. Изобразить график реализации случайного процесса с выхода блока сверточного кодера (К) на входе блока ФМС на первых 16 бинарных интервалах длительностью . Написать аналитическое выражение для случайного процесса .

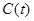
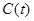
3. В соответствии с сигнальным созвездием модулятора КФМ-4 изобразить для входной реализации графики реализаций и на выходе блока ФМС случайных процессов и на символьных интервалах длительностью Написать аналитические выражения для случайных процессов и

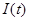
Реализацию случайного процесса

можно представить в следующей аналитической форме

где – прямоугольный импульс длительностью ,

где – прямоугольный импульс такой же формы, как , но сдвинутый вправо относительно импульса на величину , если , или влево, если ; – численный коэффициент, являющийся реализацией случайной величины на -интервале .

Последовательность КС из 16 символов: 1011 0000 0000 0011

Процессы и можно представить в виде

; ,

где – прямоугольный импульс длительностью (рис. 3.4.2., б); – символьный интервал; – бинарный интервал.

где – прямоугольный импульс такой же формы, как импульс , но сдвинутый вправо относительно импульса на величину nT_s, если , или влево, если ; и – независимые случайные величины, заданные на символьном интервале с номером , которые согласно сигнальному созвездию (рис. 3.4.1) принимают два дискретных значения , , 3h, -3h с вероятностью 0,25 каждое, т.е.

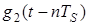
Рис. 3.4.2. Реализации и случайных процессов и

4. Написать аналитические выражения для корреляционной функции и спектральной плотности мощности входного случайного процесса и построить графики этих функций.

= .

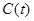
5. Написать аналитические выражения для корреляционных функций и , спектральных плотностей мощности и случайных процессов и Построить графики этих функций.

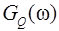
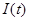
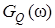
Рис. 3.4.3. график корреляционной функции

Рис. 3.4.4. график функции спектральной мощности

6. Сравнить графики корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала.

Теорема Хинчина — Колмогорова (также известная как Теорема Винера — Хинчина и иногда как Теорема Винера — Хинчина — Эйнштейна) утверждает, что спектральной плотностью мощности стационарного в широком смысле случайного процесса является преобразование Фурье соответствующей автокорреляционной функции

Теорема удобна для анализа линейных стационарных систем, где входные и выходные значения не интегрируемы в квадратурах, из-за чего преобразований Фурье не существует. Как следствие, преобразование Фурье автокорреляционной функции выходного сигнала ЛСС-системы равно произведению преобразования Фурье автокорреляционной функции входного сигнала системы на квадрат модуля преобразования Фурье её импульсной характеристики. Это выполняется даже когда преобразований Фурье входных и выходных сигналов не существует, из-за того что они не интегрируемы. Поэтому входные и выходные параметры не могут быть прямо связаны преобразованием Фурье импульсной передаточной функции.

Из того, что преобразование Фурье автокорреляционной функции сигнала есть спектр мощности сигнала, следует, что спектр мощности выходного сигнала равен произведению спектра мощности входного и передаточной функции системы.

Это следствие используется в нахождении спектра мощности параметрическим методом.

Модулятор

В состав модулятора входят блоки-перемножители, инвертор и сумматор, на выходе которого получаем сигнал заданного вида модуляции КАМ-16.

1. Построить графики гармонических колебаний и на четырех символьных интервалах ( ). При этом на символьном интервале длительностью укладывается два периода частоты .

2. На этих же интервалах 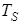нарисовать графики сигналов

;

;

3. На этих же интервалах 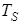изобразить график сигнала заданной квадратурной модуляции на выходе сумматора в квазигармонической форме, выделив из полученной суммы четыре слагаемых с номерами . Фазы определять по сигнальному созвездию.

I(t)= <-h,h,h,-h>q(t)= <-3h,h,h,-3h>– значения I(n) и Q(n) на промежутке n=0…3.

Рис. 3.5.1. графики сигналов

4. Написать аналитические выражения для корреляционных функций , для случайных сигналов и на выходах перемножителей, где случайная фаза с равномерной плотностью вероятности на интервале . Случайная фаза не зависит от случайных процессов и .

.

.

5. Написать аналитические выражения для корреляционной функции сигнала и для спектральной плотности мощности сигнала КФМ-4 на выходе сумматора. Построить графики этих функций.

Строим графики функций

Рис. 3.5.2. график функции корреляции на выходе сумматора

Рис. 3.5.3. график функции спектральной плотности мощности

Непрерывный канал

В КР непрерывный канал (НК) рассматривается практически по той же методике, как в предыдущей КР [14].[1]

Передача сигнала происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии аддитивной помехи типа гауссовского белого шума. Сигнал на выходе такого канала имеет вид

где – коэффициент передачи канала. Для всех вариантов . Односторонняя спектральная плотность мощности помехи равна = 1.85 10 -7

1. Определить минимально необходимую ширину полосы частот непрерывного канала .

=0.035

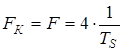
2. Определить мощность помехи на выходе канала.

F=T_s+f_c a=2

3. Определить среднюю мощность сигнала и найти отношение / .

=1?145 10 7

=1312 10 5

=5.162 10 9

4. Рассчитать пропускную способность (за секунду) непрерывного канала.

=1.168

5. Оценить эффективность использования пропускной способности непрерывного канала.

, где Н’=2fв 1,443 L

Демодулятор

1. Изобразить структурную схему когерентного демодулятора, оптимального по критерию максимального правдоподобия для КАМ -16.

Рис. 3.7.1 структурная схема

2. Написать алгоритмы работы решающих устройств РУ в составе когерентного демодулятора.

Формирователь квадратур (ФК) состоит из двух перемножителей (фазовых детекторов), двух фильтров нижних частот (ФНЧ) и фазовращателя опорного колебания на 90 (ФВ).

Фильтр основной селекции демодулятора может быть реализован как на промежуточной частоте, так на видеочастоте, то есть это может быть как фильтр УПЧ, так и фильтры низкой частоты ФК.

Частота дискретизации сигналов в АЦП равна удвоенной тактовой частоте входного сигнала: f_д= 2f_т. Формирование на выходе АЦП двух отсчетов сигнала за длительность одного информационного символа T_с= 1/f_т необходимо для работы временного дискриминатора УТС.

Устройство выделения информации (УВИ) содержит делитель тактовой частоты на 2 (ДЧ), два устройства (делителя на 2), осуществляющих прореживание сигнала (на выходы этих устройств поступает каждый второй отсчет входных сигналов), два решающих устройства (РУ), которые формируют выходные данные квадратурных каналов, и дифференциальный декодер. Разрядность данных на выходе РУ определяется позиционностью КАМ-М сигнала M и равна (log₂M)/2.

В некоторых случаях при реализации демодулятора сигнал на временной дискриминатор УТС и на амплитудный детектор АРУ снимается с выходов формирователя квадратур. При этом устройства тактовой синхронизации и автоматической регулировки усиления являются полностью аналоговыми.

В состав УВИ можно добавить корректор межсимвольных искажений, который подключают к выходам АЦП (T_с/2-интервальный корректор) или к выходам устройств прореживания (T_с-интервальный корректор).

3. Определить вероятности ошибок на выходах РУ1 и РУ2 при определении значений символов и , равных –h, h, -3h, 3h:

= = = ;

= = = ,

где – обозначение вероятности ошибочного приема, если

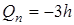4. На четырех символьных интервалах длительностью 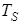нарисовать сигналы на выходах РУ1 и РУ2 демодулятора, соответствующие сигналам на выходе блока ФМС, которые поступают на два входа преобразователя параллельного кода в последовательный код. Под двумя построенными графиками, используя сигнальное созвездие для заданного вида модуляции, изобразить график сигнала на выходе преобразователя в виде соответствующей последовательности прямоугольных импульсов длительностью (разд. 4.5).

На вход демодулятора поступает последовательность импульсов:

Генератор вырабатывает сигнал на интервале с номером , а на интервале с номером – сигнал .

В момент окончания символьного интервала длительностью решающее устройство (РУ1) сравнивает 2 входных напряжения равенств и выбирает из них максимальное, тем самым реализуя правило принятия решения.

Получаем последовательность импульсов на РУ1: <-h,h,h,h>; Получаем последовательность импульсов на РУ2: ; Выбираем максимальное из каждой пары, строим последовательность импульсов рис. 3.7.2.:

Рис. 3.7.2. сигналы на выходах РУ1 и РУ2

5. Определить вероятности ошибок на выходах РУ1 и РУ2 для значений сигналов и , равных при условии

= = =

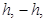
6. Определить вероятности ошибок на выходе преобразователя параллельного кода в последовательный код (ФМС) для заданных параметров сигналов и :

= = =

Выбираем из таблицы 3 соответствующую формулу, получаем:

7. Определить среднюю вероятность ошибки на выходе преобразователя.

Декодер

1. Изучить алгоритм сверточного декодирования по методу Витерби [7, с. 23–37].

В этом методе декодирования вместо кодового дерева используется решетчатая структура. Было установлено, что алгоритм Витерби является методом динамического программирования (которое уже было известно в то время), примененным к сверточным кодам. Сверточное кодирование, применяемое вместе с декодированием Витерби, в настоящее время стало одним из наиболее широко используемых на практике методов исправления ошибок.

С целью реализации устойчивой работы кодера при сверточном декодировании периодически проводят очистку (промывку) регистра сдвига кодера от информационных символов путем подачи на кодер некоторого количества нулевых символов (не информационных). Эта операция называется периодическим отбрасыванием. Следующая партияинформационных символов поступает на кодер, когда все ячейки регистра сдвига находятся в нулевом состоянии, т.е. в состоянии а=00. Обозначим:

1) — последовательность информационных символов, поступивших на вход кодера;

2) — последовательность кодовых символов с выхода кодера, которая передавалась по каналу;

3) — принятая последовательность, полученная с выхода демодулятора и поступившая на вход декодера.

С учетом сказанного рассмотрим алгоритм сверточного декодирования Витерби с использованием решетчатой диаграммы. Декодирование начинается в момент . В результате очистки кодера между сообщениями будем считать, что декодер находится в начальном состоянии а=00.

2. Используя табл. 2, написать численные значения принятых кодовых символов (ПКС). Выписанные численные значения образуют последовательность , соответствующую последовательности (11) в [7, с. 24]. Один символ в последовательности принят ошибочно и в процессе декодирования эту ошибку необходимо исправить. Для своего варианта порядковый номер символа q=3 находим в данных КР и отмечаем крестиком.

1. Построить решетчатую диаграмму декодера последовательности по аналогии с решетчатой диаграммой декодера [7, рис. 10]. Численные обозначения над ребрами решетчатой диаграммы определяются для последовательности своего варианта.

Ошибка в 1-м символе. Следовательно. Получаем последовательность:

=0*1 10 11 00 00 00 00 00 11

Решетчатая диаграмма декодера отличается от решетчатой диаграммы кодера тем, что ребрам этих решеток соответствуют разные обозначения. Числа над ребрами решетки декодера определяются, как расстояния Хемминга между двумя символами принятой последовательности , расположенными над данным ребром и двумя символами, которыми отмечено данное ребро на решетке кодера. Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной. Например, HD( 100, 001) = 2.

Рис. 3.8.1. Решеточная диаграмма декодера

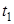
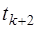
2. Построить диаграммы выживших путей от момента времени до момента времени по аналогии с решетчатыми диаграммами [7, рис. 11–17], когда от момента до момента выживает только один путь.

Выделим часть пути до момента времени t=3.

Рис. 3.8.2. часть решеточной диаграммы

Определим по диаграмме на рис.3.8.2 метрику путей по Хеммингу, исходящих из одной точки и приходящих в узлы e,f,g,h.

Выбираем наиболее короткие пути как выжившие, выделим их желтым цветом.

Рис. 3.8.3. выжившие пути

3. Перенести один выживший путь от момента времени до момента t₅ с решетчатой диаграммы декодера на решетчатую диаграмму кодера. По этому пути на диаграмме кодера определить те кодовые символы, которые поступали на вход сверточного кодера и передавались по каналу связи от момента до момента , соответствующие принятым кодовым символам с учетом исправленной ошибки.

Рис.3.8.4. наложение диаграмм.

Проследить по диаграмме, что ошибка, отмеченная крестиком, исправлена.

4. По выжившему пути, перенесенному на решетчатую диаграмму кодера, определить соответствие информационным символам 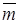, которые поступали на вход сверточного кодера, принятых кодовых символов с учетом исправленной ошибки.

Декодер принимает решение, что на интервале от до t₂ по каналу передавалась последовательность кодовых символов, соответствующая выжившему пути т.е.: 01 10 11 00 00 00 00 00 11 . Эта последовательность совпадает с последовательностью:

=11 10 11 00 00 00 00 00 11

от момента до t₂. Таким образом, ошибки, возникшие на выходе демодулятора, оказываются исправленными.

Список использованной литературы

1. Зюко, А. Г. Теория передачи сигналов / А. Г. Зюко, Д. Д. Кловский, М. В. Назаров, Л. М. Финк. – Изд. 2-е, перераб. и дополнен. – М. : Радио и связь, 1986. – 304 с.

2. Зюко, А. Г. Теория электрической связи : учебник для вузов / А. Г. Зюко, Д. Д. Кловский, В. И. Коржик, М. В. Назаров. – М. : Радио и связь, 1998.

3. Скляр, Бернард. Цифровая связь. Теоретические основы и практическое применение : пер. с англ. / Бернард Скляр. – Изд. 2–2, испр. – М. : Издательский дом «Вильямс», 2003. – 1104 с.

4. Кларк, Дж. Кодирование с исправлением ошибок в системах цифровой связи / Дж. Кларк, мл. Дж. Кейн : пер. с англ. С. И. Гельфонда ; под ред. Б. С. Цыбакова. – М. : Радио и связь, 1987. – Вып. 28. – 392 с.

5. Григоровский, Л. Ф. Теория электрической связи. Модели сигналов и методы их преобразования в системах связи : учеб. пособие / Л. Ф. Григоровский, В. И. Коржик, В. Г. Красов, В. Ф. Кушнир. – Л. : ЛЭИС. – 1990.

6. Тихонов, В. И. Статистическая радиотехника / В. И. Тихонов. – Изд. 2-е, перераб. и дополнен. – М. : «Радио и связь», 1982. – 624 с.

7. Куликов, Л. Н. Теория электрической связи. Основы сверточного кодирования : учеб. пособие / Л. Н. Куликов, М. Н. Москалец. – СПб., 2006.

2. СИСТЕМА ЦИФРОВОЙ СВЯЗИ.. 3

3. ИСХОДНЫЕ ДАННЫЕ. 5

3.1. Источник сообщения. 6

3.2. Аналого-цифровой преобразователь. 10

3.4. Формирователь модулирующих символов. 15

3.5. Модулятор. 21

3.6. Непрерывный канал. 25

3.7. Демодулятор. 27

4. Список использованной литературы.. 37

Источник