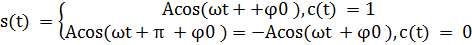Сигнальное созвездие
Содержание
Описание
Радиосигнал представляется в виде двухмерной точечной диаграммы на комплексной плоскости, точками на которой являются все возможные символы, представленные в геометрической форме. Более абстрактно, на диаграмме отмечены все значения, которые могут быть выбраны данной схемой манипуляции, как точки на комплексной плоскости. Сигнальные созвездия, полученные в результате измерения радиосигнала, могут использоваться для определения типа манипуляции, рода интерференции и уровня искажений.
| Двоичная фазовая манипуляция (BPSK) | Квадратурная фазовая манипуляция (QPSK) | Восьмеричная фазовая манипуляция (8-PSK) | Сигнальное созвездие для прямоугольной 16-КАМн. |
При представлении передаваемого символа в виде комплексного числа и при модуляции синусного и косинусного сигнала несущей частоты соответственно действительной и мнимой частями, символ можно передать двумя несущими с одной частотой. Часто такие несущие называются квадратурными. Когерентный детектор (англ.) способен демодулировать обе несущие независимо. Принцип использования двух независимо модулируемых несущих лежит в основе квадратурной модуляции. В простой фазовой манипуляции, фаза модулирующего символа становиться фазой несущего сигнала.
Если символы представлены в виде комплексных чисел, их можно представить в виде точек на комплексной плоскости. Действительная и мнимая оси часто называют in phase или I-осью и quadrature (квадратурной) или Q-осью. При нанесении на диаграмму точек от нескольких символов можно получить сигнальное созвездие. Точки на диаграмме часто называют сигнальными точками (или точками созвездия). Они представляют множество модулирующих символов, то есть модулирующий алфавит.
Решётчатая кодированная модуляция
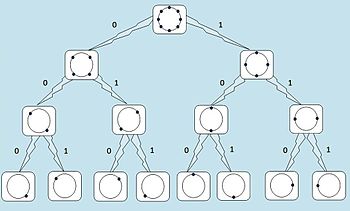
При использовании блочного или свёрточного кодирования помехоустойчивость радиосвязи повышается за счёт расширения полосы частоты и усложнения радиоаппаратуры без повышения отношения сигнал/шум (ОСШ). Для сохранения помехоустойчивости при том же значении ОСШ можно уменьшить используемую полосу частот и упростить радиоаппаратуру можно с помощью применениния решётчатой кодированной модуляции (TCM), которая впервые была разработана в 1982 году Унгербоком. В основе TCM лежит совместный процесс кодирования и модуляции.
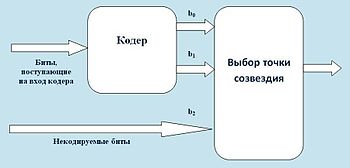
Если в используется комбинированный кодер/модулятор, общая структура которой показана на рисунке, то бит b0 позволяет выбрать одно из двух созвездий, которые получились при первом разделении. Далее выбор определяется в зависимости от бит b1 и b2.
| Фазомодулированный сигнал имеет вид: | |
| s(t)= Acos(ωt +φ(t)+φ0), | (2) |
где A и φ0 – постоянные, ω – несущая частота.
Информация кодируется фазой φ(t) . Так как при когерентной демодуляции в приемнике имеется восстановленная несущая sC (t) = Acos(ωt +φ0 ) , то путем сравнения сигнала (2) с несущей вычисляется текущий сдвиг фазы φ(t) . Изменение фазы φ(t) взаимнооднозначно связано с информационным сигналом c(t).
Двоичная фазовая модуляция (BPSK – BinaryPhaseShiftKeying)
Множеству значений информационного сигнала <0,1>ставится в однозначное соответствие множество изменений фазы <0, π>. При изменении значения информационного сигнала фаза радиосигнала изменяется на 180º. Таким образом, сигнал BPSK можно записать в виде
Следовательно, s(t)= A⋅2(c(t)-1/2)cos(ωt + φ0) .Таким образом, для осуществленияBPSK модуляции достаточно умножить сигнал несущей на информационный сигнал, который имеет множество значений <-1,1>. На выходе baseband-модулятора сигналы
Временная форма сигнала и его созвездие показаны на рис.3.
Рис. 12.Временная форма и сигнальное созвездие сигнала BPSK:a– цифровое сообщение; б – модулирующий сигнал; в – модулированное ВЧ-колебание; г– сигнальное созвездие
Квадратурная фазовая модуляция (QPSK – QuadraturePhaseShiftKeying)
Квадратурная фазовая модуляция является четырехуровневой фазовой модуляцией (M=4), при которой фаза высокочастотного колебания может принимать 4 различных значения с шагом, кратным π / 2 .
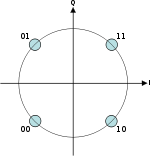
Соотношение между сдвигом фазы модулированного колебания из множества <±π / 4,±3π / 4>и множеством символов цифрового сообщения <00, 01, 10, 11>устанавливается в каждом конкретном случае стандартом на радиоканал и отображается сигнальным созвездием, аналогичным рис.4. Стрелками показаны возможные переходы из одного фазового состояния в другое.
Рис. 13. Сигнальное созвездие модуляции QPSK
Из рисунка видно, что соответствие между значениями символов и фазой сигнала установлено таким образом, что в соседних точках сигнального созвездия значения соответствующих символов отличаются лишь в одном бите. При передаче в условиях шума наиболее вероятной ошибкой будет определение фазы соседней точки созвездия. При указанном кодировании, несмотря на то, что произошла ошибка в определении значения символа, это будет соответствовать ошибке в одном (а не двух) бите информации. Таким образом, достигается снижение вероятности ошибки на бит. Указанный способ кодирования называется кодом Грея.
Многопозиционная фазовая модуляция (M-PSK)
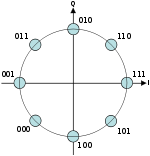
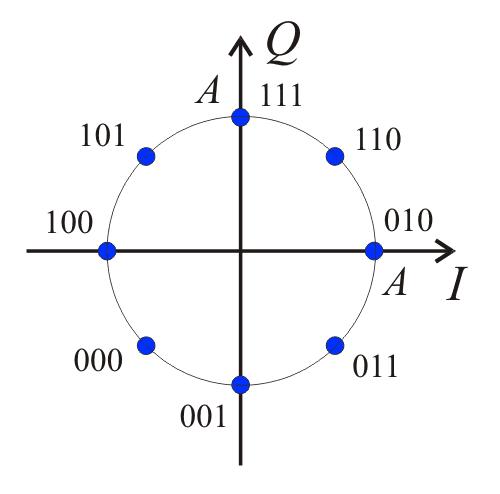
M-PSK формируется, как и другие многопозиционные виды модуляции, путем группировки k = log2M бит в символы и введением взаимно-однозначного соответствия между множеством значений символа и множеством значений сдвига фазы модулированного колебания. Значения сдвига фазы из множества отличаются на одинаковую величину. Для примера на рис.4 приведено сигнальное созвездие для 8-PSK с кодированием Грея.
Рис. 14. Сигнальное созвездие модуляции 8-PSK
Амплитудно-фазовые виды модуляции (QAM)
Очевидно, для кодирования передаваемой информации можно использовать не один параметр несущего колебания, а два одновременно.
Минимальный уровень символьных ошибок будет достигнут в случае, если расстояние между соседними точками в сигнальном созвездии будет одинаковым, т.е. распределение точек в созвездии будет равномерным на плоскости. Следовательно, сигнальное созвездие должно иметь решетчатый вид. Модуляция с подобным видом сигнального созвездия называется квадратурной амплитудной модуляцией (QAM – QuadratureAmplitudeModulation).
QAM является многопозиционной модуляцией. При M=4 она соответствует QPSK, поэтому формально считается для QAM M ≥ 8 (т.к. число бит на символ k = log2M ,k∈N , то M может принимать только значения степеней 2: 2, 4, 8, 16 и т.д.). Для примера на рис.5 приведено сигнальное созвездие 16-QAM с кодированием Грея.
Рис. 15. Сигнальное созвездие модуляции 16 –QAM
Частотные виды модуляции (FSK, MSK, M-FSK, GFSK, GMSK).
В случае осуществления частотной модуляции параметром несущего колебания – носителем информации – является несущая частота ω(t) . Модулированный радиосигнал имеет вид:
| s(t)= Acos(ω(t)t +φ0)= Acos(ωc t +ωd c(t)t +φ0)= |