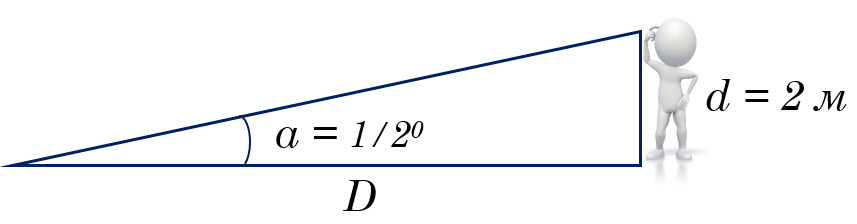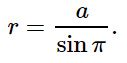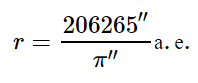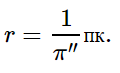Солнце оценка угловых расстояний
Работа N 7. Определение угловых и линейных размеров Солнца (или Луны)
I. С помощью теодолита.
1. Установив прибор и вставив светофильтр в окуляр трубы, совместить нуль алидады с нулем горизонтального лимба. Закрепить алидаду и при открепленном лимбе навести трубу на Солнце так, чтобы вертикальная нить касалась правого края диска Солнца (это достигается с помощью микрометрического винта лимба). Затем быстрым вращением микрометрического винта алидады перевести вертикальную нить на левый край изображения Солнца. Сняв показания с горизонтального лимба, и получают угловой диаметр Солнца.
2. Вычислить радиус Солнца по формуле:
R = D ∙ sin r
где r — угловой радиус Солнца, D — расстояние до Солнца.
3. Для вычисления линейных размеров Солнца можно воспользоваться и другой формулой. Известно, что радиусы Солнца и Земли связаны с расстоянием до Солнца соотношением:
R = D ∙ sin r ,
R0 = D ∙ sin p,
где r — угловой радиус Солнца, а p — его параллакс.
Поделив почленно эти равенства, получим:
Ввиду малости углов, отношение синусов можно заменить отношением аргументов.
Тогда 
Значения параллакса р и радиуса Земли берутся из таблиц.
| R0= 6378 км, |  |
| r = 16′ | |
| p = 8″,8 |
Отношение 
Аналогично определяются и размеры Луны.
II. По времени прохождения диска светила через вертикальную нить оптической трубы
Если смотреть на Солнце (или Луну) в неподвижный телескоп, то вследствие суточного вращения Земли светило будет постоянно уходить из поля зрения телескопа. Для определения углового диаметра Солнца, с помощью секундомера измеряют время прохождения его диска через вертикальную нить окуляра и найденное время умножают на cos d , где d — склонение светила 1 . Затем время переводят в угловые единицы, помня, что за 1 мин Земля поворачивается на 15′, а за 1 сек. — на 15″. Линейный диаметр D определяется из соотношения:

где R — расстояние до светила, a — его угловой диаметр, выраженный в градусах.
Если использовать угловой диаметр, выраженный в единицах времени (например, в секундах), то
где t — время прохождения диска через вертикальную нить, выраженное в секундах.
Дата наблюдения — 28 октября 1959 г.
Время прохождения диска через нить окуляра t = 131 сек.
Склонение Солнца на 28 октября d = — 13њ.
Угловой диаметр Солнца a = 131∙ cos 13њ = 131∙0,9744 = 128 сек. или в угловых единицах a = 32 = 0,533њ.
| Линейный диаметр Солнца |  |
1. Из двух способов второй более доступен. Он проще по технике выполнения и не требует какой-либо предварительной тренировки.
2. Проводя такие измерения, интересно отметить разницу в величине видимого диаметра Солнца, когда оно бывает в перигее и апогее. Разница эта составляет около 1′ или по времени — 4 сек.
В значительно больших пределах изменяется видимый диаметр Луны (от 33′,4 до 29′,4). Это хорошо видно из рис. 55. Здесь уже разница во времени — около 16 сек.

Рис. 55. Наибольший и наименьший видимые размеры диска Луны, расположенные концентрически (слева) эксцентрически (справа).
Такие наблюдения будут воочию убеждать учащихся в том, что орбиты Земли и Луны не круговые, а эллиптические (иллюстрация к законам Кеплера).
3. Пользуясь вторым способом, можно определять размеры некоторых лунных образований, длину теней от гор и др.
Источник
Солнце оценка угловых расстояний
Почему так трудно определить размеры небесных объектов и расстояния до них? Все дело в том, что размеры удаленных объектов мы можем определить только по сравнению размерами известных объектов, а на небе нам не с чем сравнивать. Мы видим на небе множество светящихся точек, но яркость точки может определяться как ее размером, абсолютной светимостью, так и расстоянием до нее.
Поэтому в астрономии практически невозможно определить оптическими методами линейный размер удаленного объекта, можно определить только его угловой размер.
Древние греки изобрели тригонометрию, которая позволяет определить количественные соотношения между углами, линейными размерами и линейными расстояниями. С помощью простых математических соотношений, включающих базовую тригонометрию, мы можем вычислить расстояния до удаленных объектов, размеры которых известны (или размеры, если расстояния известны).
Уравнение малых углов
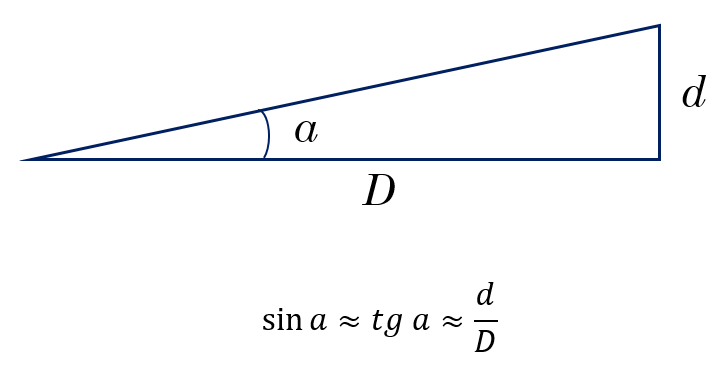
Если углы малые, то синус угла примерно равен тангенсу, который, в свою очередь примерно равен самому углу в радианной мере.
Уравнение малых углов включает в себя угловой размер объекта, его линейный размер и расстояние. Если известны какие-либо две из этих величин, можно вычислить третью. Обратимся к угловому размеру с символом a , выраженному в секундах дуги. Обозначим диаметр объекта как d , а расстояние до него как D . Тогда уравнение малого угла
a / 206 265 = d / D
Число 206 265 называется константой пропорциональности. Число 206 265 на самом деле является числом секунд дуги в угле 57,3° , который является специальным углом, называемым радианом. Радиан определяется как центральный угол дуги, длина которой равна радиусу окружности. Длина окружности равна 2πr , Радиан равен 360° / 2 π = 57,3° или около шестой части полного круга.
Вот пример использования уравнения малого угла. Предположим, что ваш друг ростом в 2 метра стоит через поле от вас, где он виден под углом ½° , или 1800″ . Как он далеко от вас? Мы хотим найти расстояние D , выразим эту величину из уранения:
D = 206 265 d / a
Используя метрические единицы, найдем
D = (2.1 x 10 5 x 2) / (1.8 x 10 3 ) = 2.3 х 10 2 метра = 230 метров
Если ваш друг имеет рост 2 метра и угловой размер его составляет ½ ° (или 1800 угловых секунд), расстояние D составляет 230 метров. Обратите внимание, что мы округляем все наши оценки до двух значащих цифр, потому что измерение угла вряд ли будет очень точным.
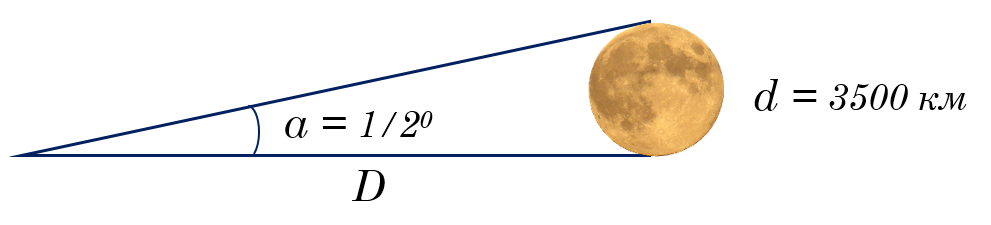
Как поняли древние греки, уравнение малого угла можно использовать для определения астрономических расстояний. Они не могли точно измерить диаметр Луны, но они знали ее угловой размер a, который также составляет примерно ½° , или 1800″ .
Если мы используем современные знания о том, что диаметр Луны составляет около 3500 километров, мы можем оценить расстояние до нее так же, как мы это сделали для расстояния друга выше. В метрических единицах d будет 3,5 × 10 6 метров. Уравнение будет гласить:
D = (2.1 × 10 5 × 3.5 × 10 6 ) / (1.8 × 10 3 ) ≈ 4 х 10 8 метров ≈ 4 x 10 5 километров.
Реальное среднее расстояние до Луны 384 000 км. Неплохая точность!
Методы определения расстояний до звезд
Годичный параллакс
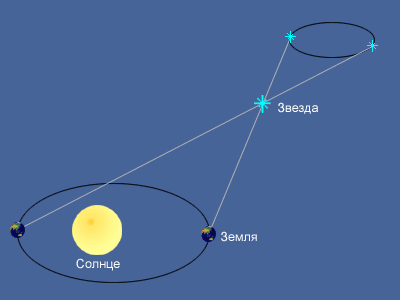
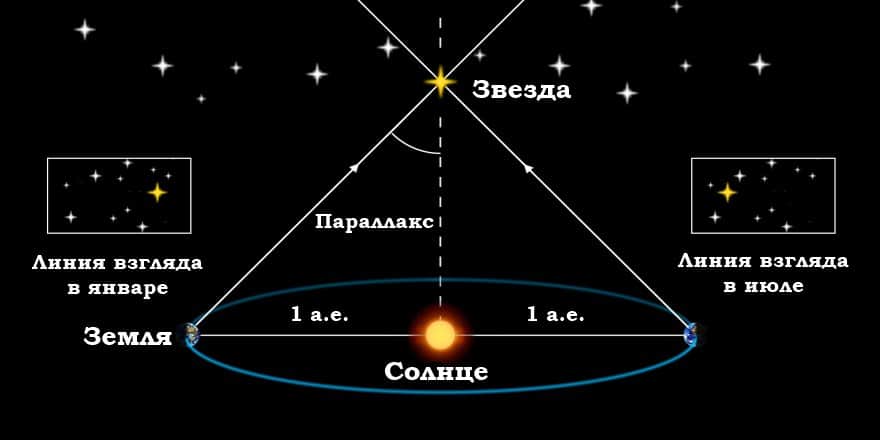
Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом ( π ).
Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.
Если CT = a есть средний радиус земной орбиты, SC = r — расстояние до звезды S от Солнца C, а угол π — годичный параллакс звезды, то
Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′ , то расстояние до звезды можно определить из соотношения
При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины — парсек (пк) , название которой происходит от слов «параллакс» и «секунда».
Парсек — это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.
1 пк = 206 265 а. е. = 3,086 · 10 13 км.
Таким образом, расстояние до звезд в парсеках будет определяться выражением
В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках ( 1 кпк = 10 3 пк ) и мегапарсеках ( 1 Мпк = 10 6 пк ), а также в световых годах ( 1 св. г. = 9,46 · 10 12 км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г. ).
Световой год — расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.
Фотометрический метод определения расстояний
Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах ( m — видимая, M — абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний rф(пк) :
Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.
Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5 m . Эта погрешность соответствует относительной погрешности 30%.
Цефеиды (стандартные свечи)
Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном свойстве переменных звезд — цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5 m . Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.
Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).
Источник
Азимут и высота солнца над горизонтом
Вычисление азимута и высоты солнца над горизонтом по заданным координатам и времени наблюдения. Возможно как задание координат вручную, так и выбор значения из справочника городов.
Продолжаем тему, начатую статьей Восход и закат солнца.
На повестке дня вычисление азимута солнца и его высоты над горизонтом в любой момент времени в точке с заданными координатами. Азимут мы откладываем от севера по часовой стрелке.
Алгоритм расчета взят отсюда. Описал его какой-то хороший швед. Он старался как мог, но все равно для стороннего человека ничего не понятно. Например, я могу еще понять, как мы переходим от одной системы координат к другой, но понять, почему долгота перигелия солнца вычисляется как
, где d — количество дней от эпохи J2000 — это уже выше моих сил.
Видимо где-то далеко, в башне из слоновой кости, сидят астрономы, и все эти цифры рассчитывают, а потом все остальные смертные их используют. Может быть какой-нибудь астроном когда-нибудь расскажет о том, как это все происходит; пока же пришлось взять на веру все эти магические цифры и воплотить расчет в жизнь. Очевидно, так делает большинство.
Есть несколько книг, которые обычно рекомендуют людям на форумах, когда не хотят отвечать развернуто, типа, «смотри вон там», и я тоже приведу их здесь:
Jean Meeus. Astronomical algorithms
Peter Duffett-Smith. Practical Astronomy with your calculator.
Как и в случае калькуляторов для расчета времени восхода и захода солнца, ниже представлены два калькулятора — первый берет информацию о координатах и часовом поясе из справочника городов, т. е. остается только выбрать город и ввести время наблюдения; а второй позволяет задать координаты и часовой пояс «вручную». Информацию о городах могут добавлять в справочник зарегистрированные пользователи.
Отрицательная высота над горизонтом соответствует темному времени суток — солнце «под» горизонтом. Пересечение с горизонтом утром происходит примерно на азимуте 90 градусов, из чего можно сделать смелый вывод, что солнце восходит все-таки на востоке.
Paul Schlyter (это швед) утверждает, что ошибка в расчетах не превышает одной угловой минуты для дат в диапазоне 1900 – 2100.
Источник